Исходные данные:

R1, Ом	R2, Ом	R3, Ом	R4, Ом	R5, Ом	E1, В	Е3, В
9	5	11	12	15	56	65

Преобразуем схему заземлив один из узлов:

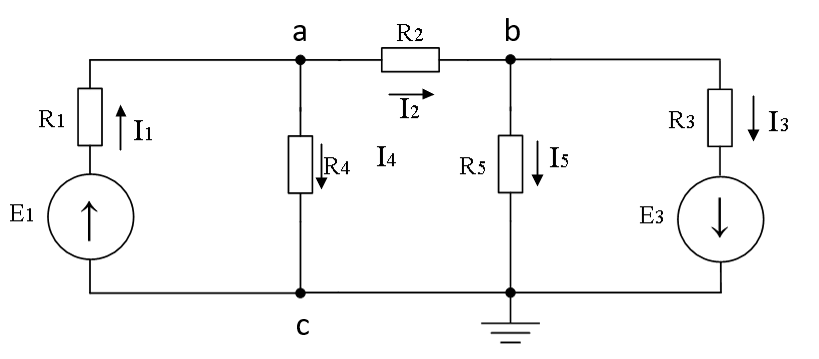
Рисунок 2 – Преобразованная схема

Заземлим узел с, т.е.

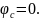
Составим систему уравнений:

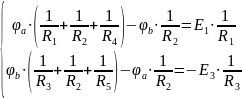
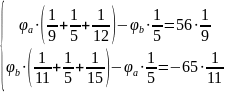
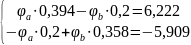
Отсюда находим потенциалы точек a и b:

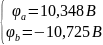
Токи в ветвях будут равны:

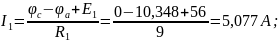
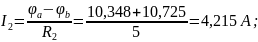
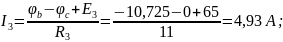
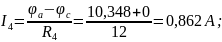
Проверим правильность решения по первому закону Кирхгофа:

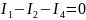
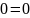
Построим потенциальную диаграмму для контура, содержащего источник ЭДС 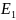. Для этого найдем потенциалы точек в контуре:

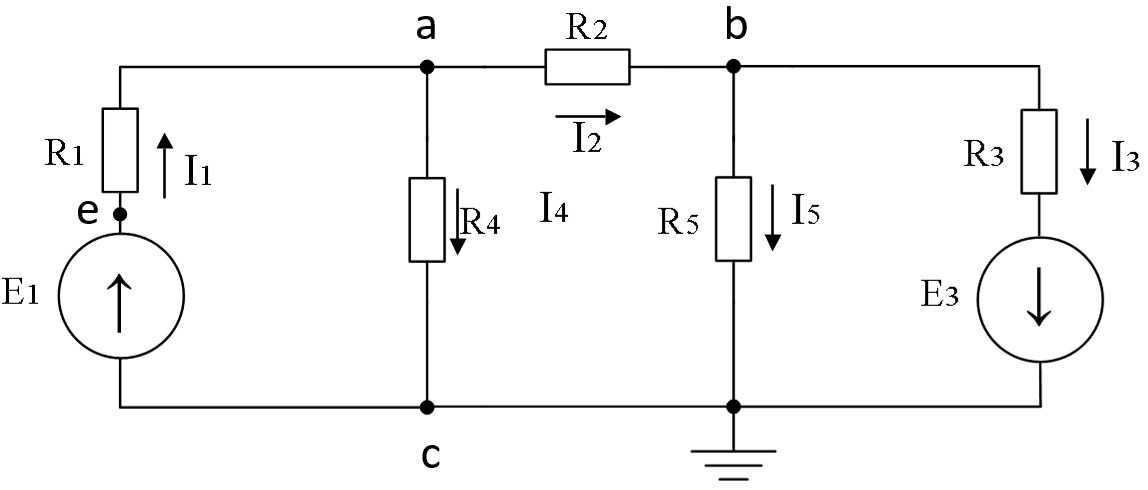
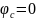
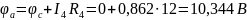
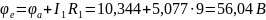
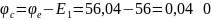
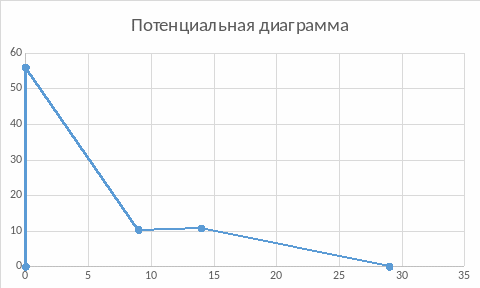
Рисунок 4 - Потенциальная диаграмма контура

Задание №4. Методом наложения вычислить токи. Составить баланс мощностей.

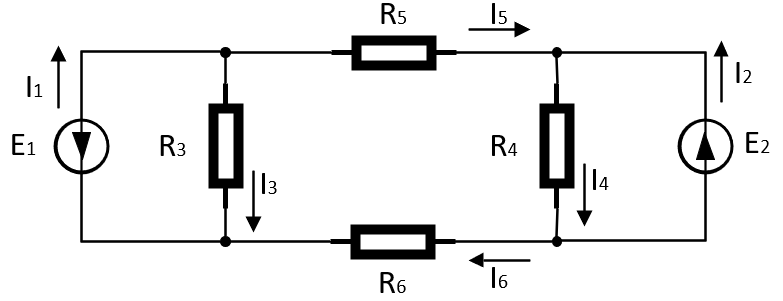
Рисунок 1 – Схема для четвертого задания

Исходные данные:

R3, Ом	R4, Ом	R5, Ом	R6, Ом	E1, В	E2, В
7	12	7	4	36	25

Исключаем из цепи E₂, при этом ток при закороченом E₂ по 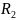идти не будет, преобразуем схему:

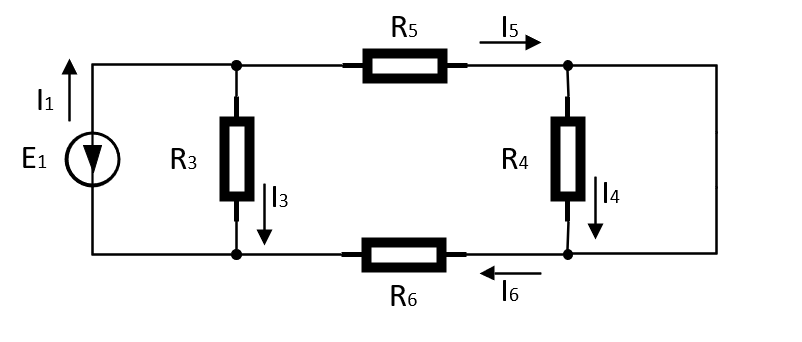
Рисунок 2 – Подсхема без источника ЭДС E₂

Преобразуем схему цепи для удобного восприятия:

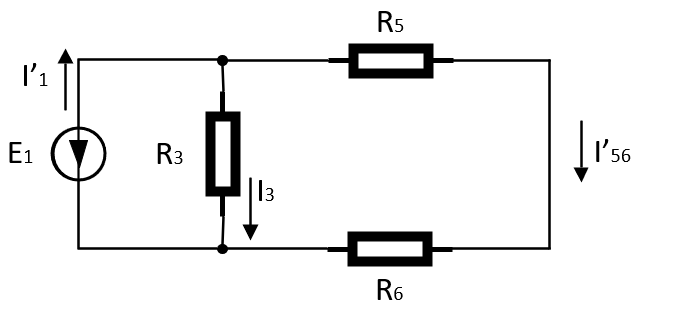
Рисунок 3 – Подсхема без источника ЭДС E₂

Находим эквивалентное сопротивление схемы без источника ЭДС E₂:

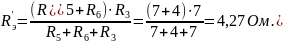
Находим токи методом эквивалентных преобразований:

.

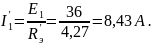
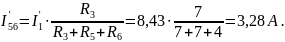
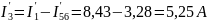Теперь исключаем из цепи E₁, при этом ток при закороченом E₁ по идти не будет, преобразуем схему:

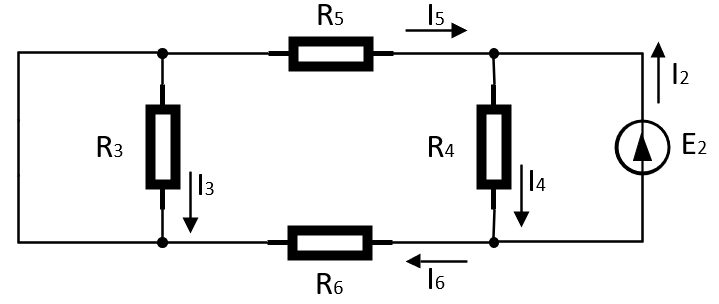
Рисунок 4 – Подсхема без источника ЭДС

Преобразуем схему цепи для удобного восприятия:

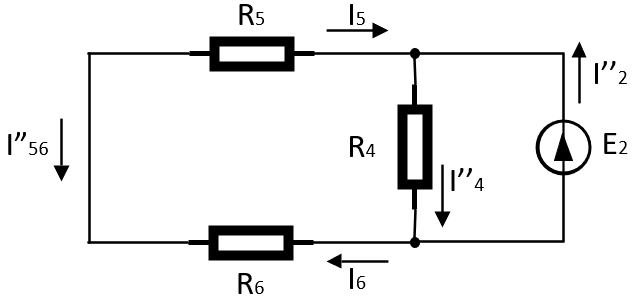
Рисунок 5 – Подсхема без источника ЭДС

Находим эквивалентное сопротивление схемы без источника ЭДС E₂:

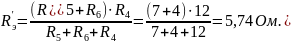
Находим токи методом эквивалентных преобразований:

.

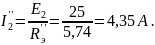
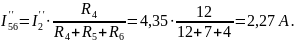
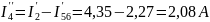Находим истинные токи:

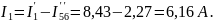
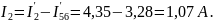
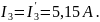
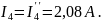
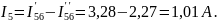
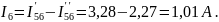
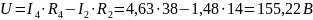
Для проверки правильности решения составим баланс мощностей для исходной схемы:

=

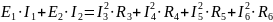
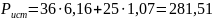
= (5,15)² 7 + (2,08)² 12 + (1,01)² 7 + (1,01)² 4 = 281,76

= доказано

Задание №5. Вычислить ток в резисторе сопротивлением методом эквивалентного генератора. Токи активного двухполюсника вычислить методом напряжения между двумя узлами.

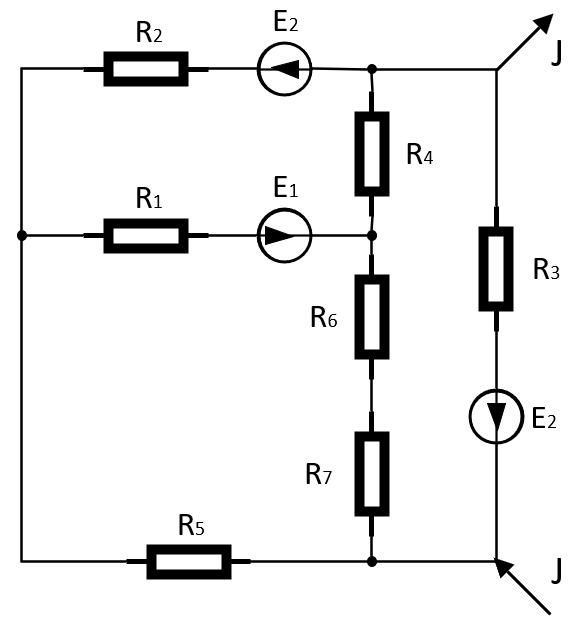
Рисунок 1 – Схема для пятого задания.

Исходные данные:

R1, Ом	R2, Ом	R3, Ом	R4, Ом	R5, Ом	R6, Ом	R7, Ом	E1, В	E2, В	E3, В	J, А
12	14	7	12	7	4	5	36	25	40	6

Визуально упростим схему:

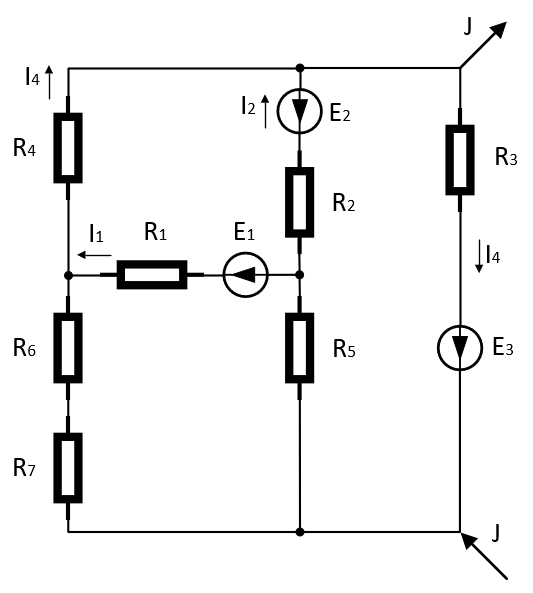
Рисунок 2 – Упрощенная схема.

Поскольку нам надо найти 𝐼₁ методом генератора мы отключим ветвь, содержащую в себе его резистор (холостой ход):

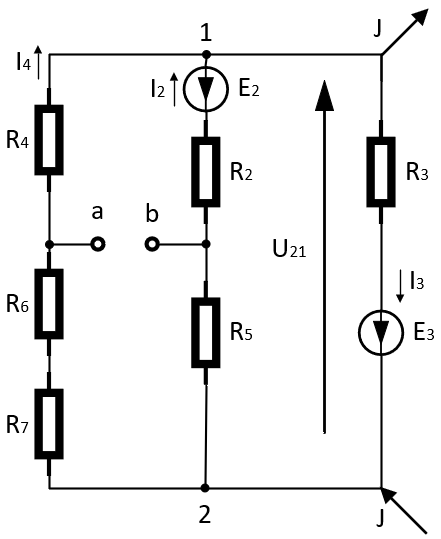
Рисунок 3 – Преобразованная схема, содержащая в себе холостой ход.

Воспользуемся методом напряжения между двумя узлами чтобы найти силу тока на каждой ветви:

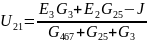, где G_i – проводимости ветвей.

.

.

.

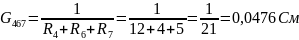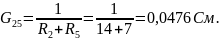
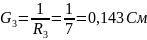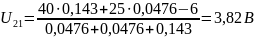По закону Ома для ветвей:

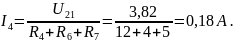
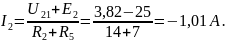
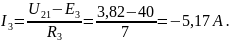
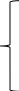
Воспользуемся методом узловых потенциалов:

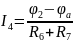
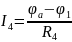
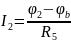
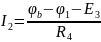
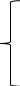
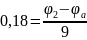
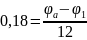
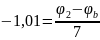
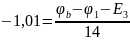
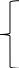
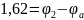
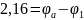
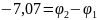
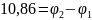
Составим матрицу по данным уравнениям:

1	2	a	b
0	-1	1	0	-1,62
-1	0	1	0	2,16
0	1	0	-1	-7,07
-1	0	0	1	10,86

Умножим первую строку и сложим с третей, в итоге получим:

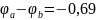
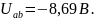
Преобразуем схему для более удобного нахождения эквивалентного сопротивления:

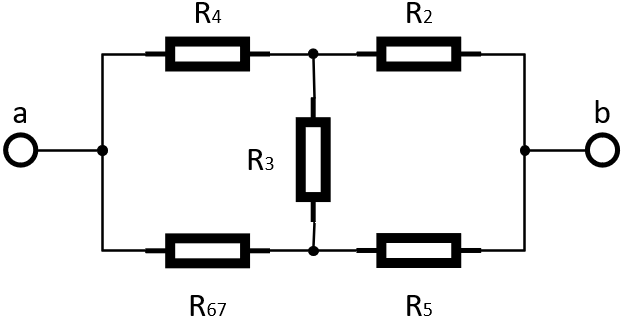
Рисунок 4 – Преобразование схемы.

Сделаем преобразование из треугольника в звезду:

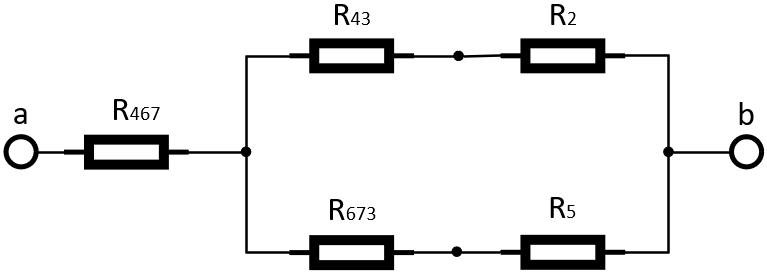
Рисунок 5 – Преобразование из треугольника в звезду.

Находим эквивалентное сопротивление:

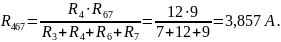
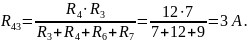
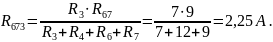
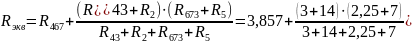
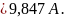
Найдем I₁:

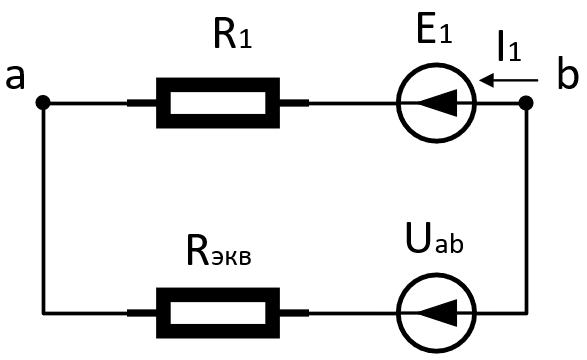
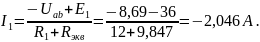
Задание №6. Определить мощность 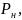выделяемую в нагрузке, при изменении ее сопротивления 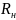. Построить график зависимость 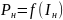, включающий режимы холостого хода и короткого замыкания. Исходные данные:

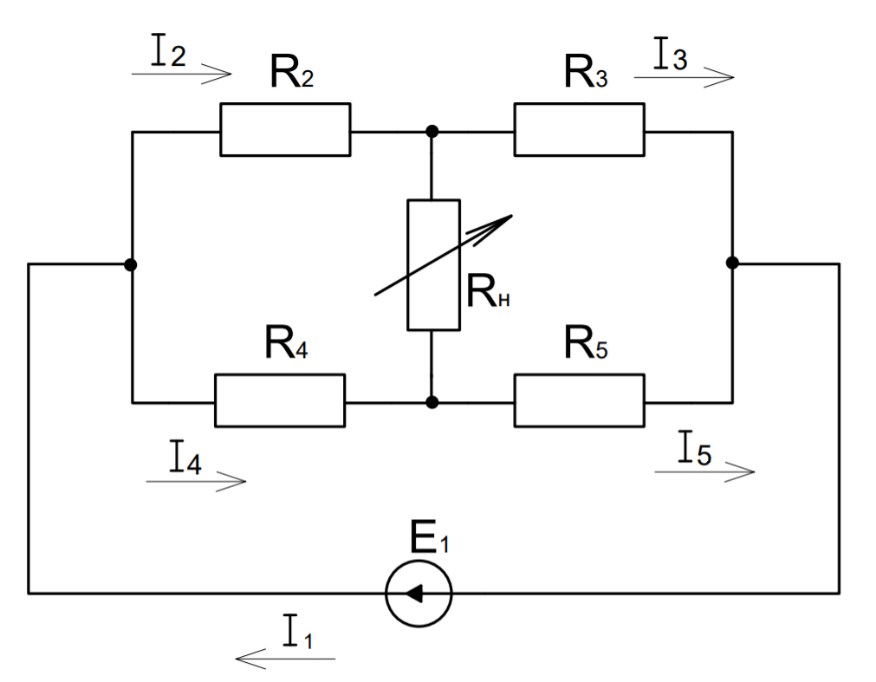
Рисунок 1 – Схема электрической цепи для шестого задания

Таблица 3 – Известные величины для шестого задания

Вел.	R2, Ом	R3, Ом	R4, Ом	R5, Ом	E1, В
Знач.	14	7	12	7	36

Данная задача решается методом эквивалентного генератора. Для нахождения тока на необходимо разорвать исследуемую ветвь для избав-ления генератора от нагрузки.

Отсоединяем ветвь ab и находим сопротивление нагрузки:

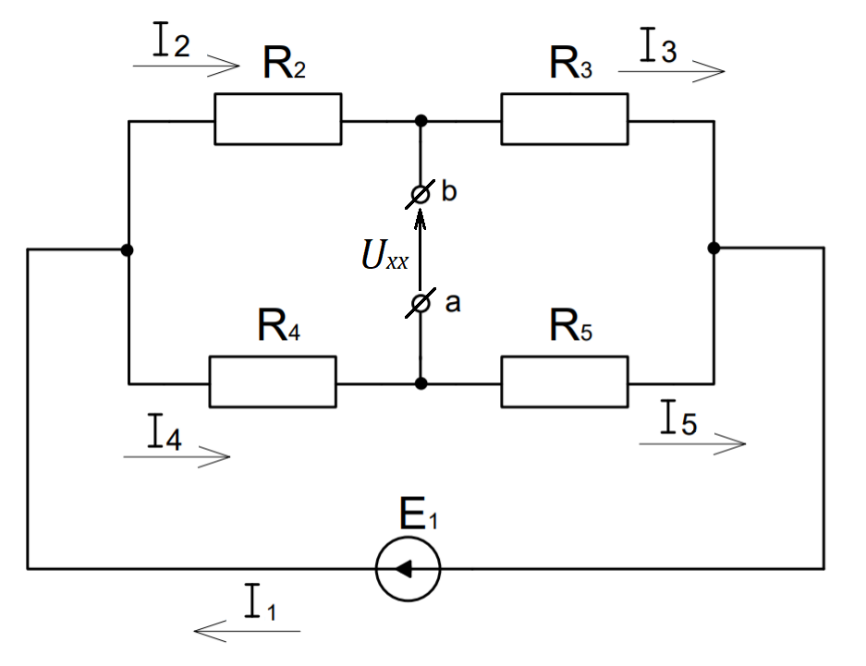
Рисунок 2 – Схема с разорванной ветвью ab

Шунтируем источник ЭДС :

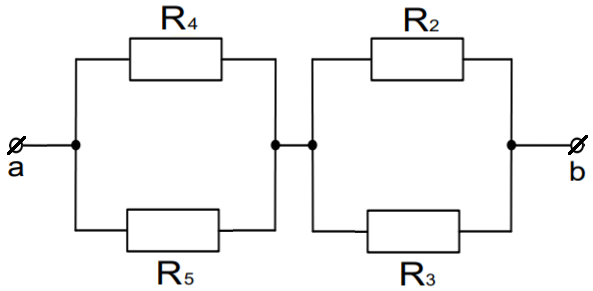
Рисунок 3 – Схема соединения резисторов

Находим по формуле сопротивление нагрузки (эквивалентное сопротив-ление или входное сопротивление):

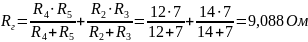
Вычисляем напряжение холостого хода :

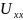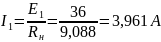
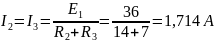
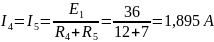
Согласно второму закону Кирхгофа

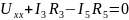
Откуда:

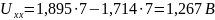
Рассчитаем ток, проходящий через нагрузку при коротком замыкании и холостом ходе:

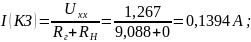
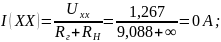
Найдём ток для ещё для 7 значений сопротивления нагрузки (от 0 до 70 Ом)

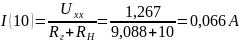
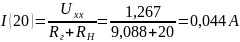
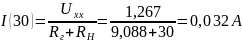
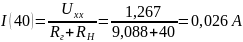
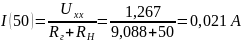
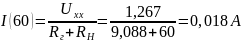
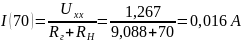
Мощность для всех значений сопротивления нагрузки равна:

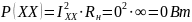
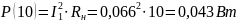
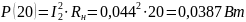
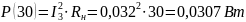
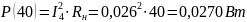
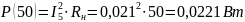
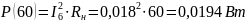
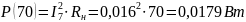
Построим график зависимости:

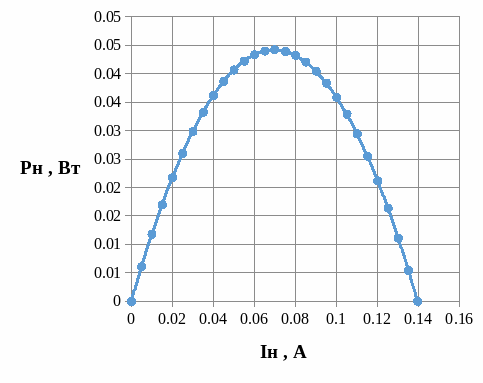
Рисунок 4 – График зависимости

Задание №7. Найти показания вольтметра.

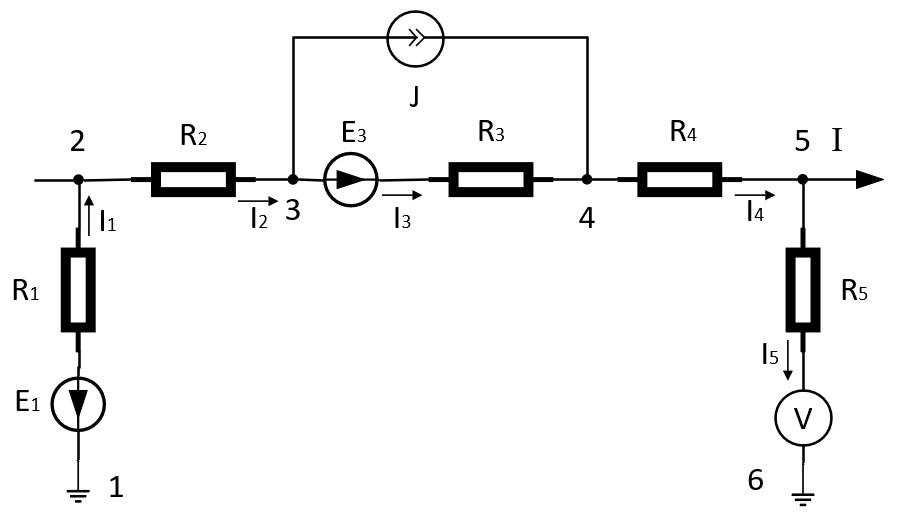
Рисунок 1 – Схема электрической цепи для седьмого задания

Исходные данные:

R1, Ом	R2, Ом	R3, Ом	R4, Ом	R5, Ом	E1, В	E2, В	J, А	I, А
12	14	7	12	7	36	25	6	2

Решение:

1. Найдём токи схемы

По ветви с токам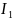и и 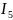ток не проходит, поскольку в цепь последова-тельно подключён идеальный вольтметр с бесконечным внутренним сопротивлением. Следовательно, токи и равны нулю.

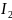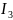По первому закону Кирхгофа найдем и и :

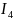1)

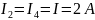
2)

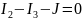
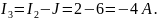
2. Найдём показания вольтметра

По второму закону Кирхгофа:

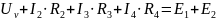
Откуда:

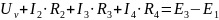
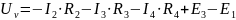
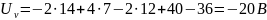
Показания вольтметра найдены, задача решена.