
Задача 6
Определить
мощность
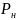 ,
выделяемую в нагрузке, при изменении
её сопротивления
,
выделяемую в нагрузке, при изменении
её сопротивления
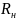 .
Построить график зависимости
.
Построить график зависимости
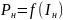 ,
включающий режимы холостого хода и
короткого замыкания.
,
включающий режимы холостого хода и
короткого замыкания.
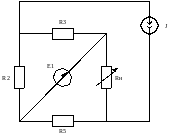
Рисунок 6.1 – Исходная схема к заданию 6
Ток нагрузки в соответствии со схемой равен:
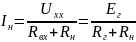
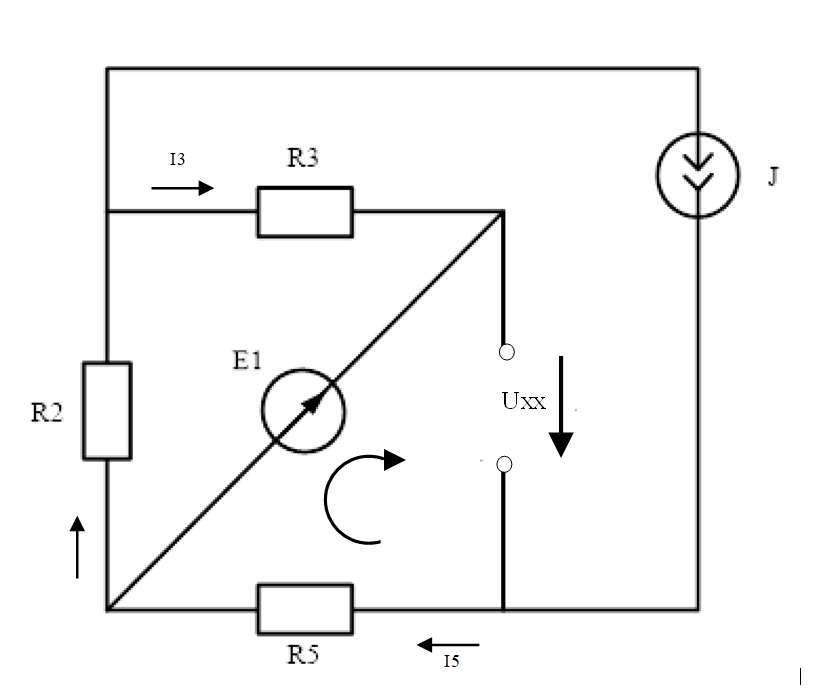
Рисунок 6.2 - Схема с разрывом в ветви с изменяемой нагрузкой
ЭДС эквивалентного генератора равно напряжению холостого хода в цепи с разрывом:
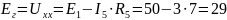 В
В
где
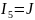 .
.
Сопротивление эквивалентного генератора равно входному сопротивлению цепи и определяется в соответствии со схемой:
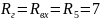 Ом
Ом
Ветвь с источником тока разрывается, ЭДС – шунтируется.
Определим закон, по которому будет изменяться мощность в зависимости от тока:
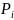 =
=
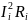
Построим график (рисунок 6.3) в зависимости от сопротивления, расчётные данные представлены в таблице 6.
Таблица 6 – Данные для построения графика зависимости
, Ом |
0 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
|
|
4,14 |
1,70 |
1,07 |
0,78 |
0,62 |
0,51 |
0,43 |
0,38 |
0,33 |
0 |
, Вт |
0 |
28,9 |
22,9 |
18,25 |
15,38 |
13,01 |
11,09 |
10,12 |
8,71 |
0 |
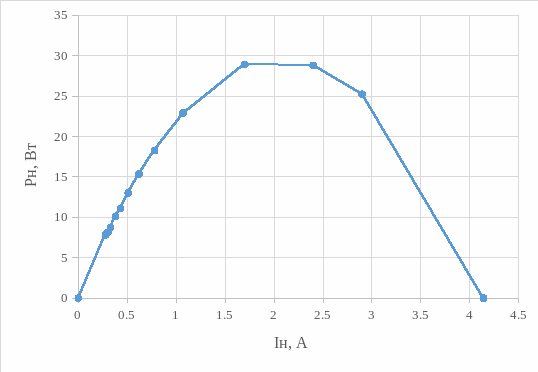
Рисунок 6.3 – График зависимости
Задача 7
Найти показания вольтметра.
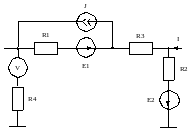
Рисунок 7.1 – Исходная схема к заданию 7
Укажем на схеме направление тока и обход контура:
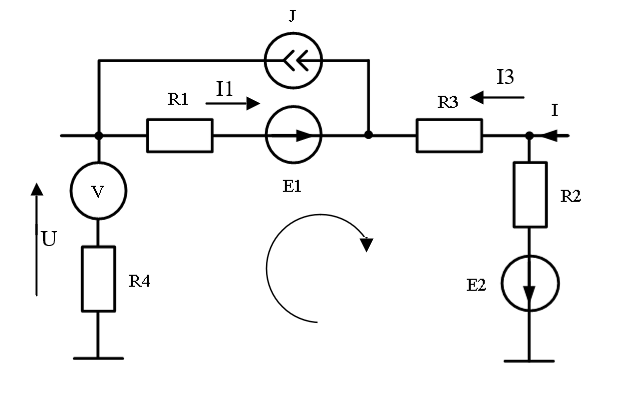
Рисунок 7.2 – Схема с обозначением тока
Запишем второй закон Кирхгофа:
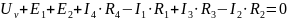
где
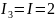 А
А
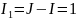 А
А
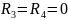 ,
так как вольтметр размыкает цепь.
,
так как вольтметр размыкает цепь.
Тогда,
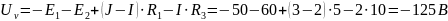
Знак минус показывает, что истинное напряжение вольтметра направлено в противоположную сторону.
Задача 8
Вычислить токи наиболее рациональным методом. Любым путём проверить правильность решения.
Задача решена методом контурных токов.
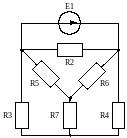
Рисунок 8.1 – Исходная схема к заданию 8
Преобразуем источник ЭДС в источник тока:
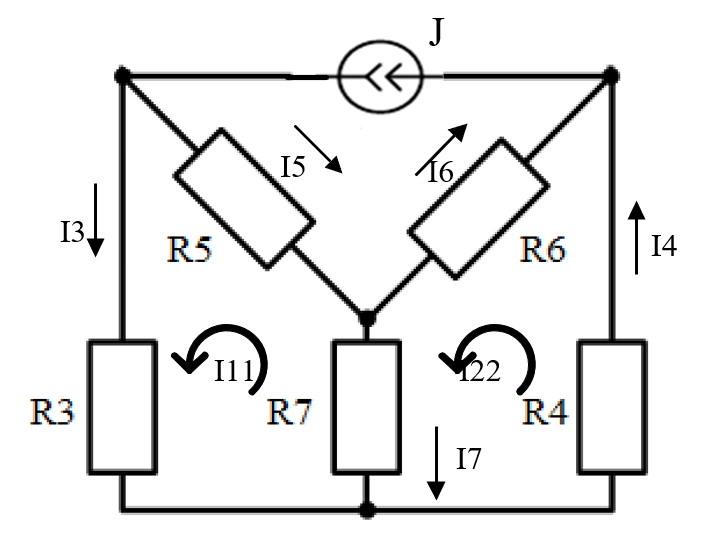
Рисунок 8.2 – Преобразованный источник тока
В этом случае источник тока равен:
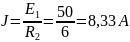
Система уравнений для контурных токов (рисунок 8.2) имеет следующий вид:

Перепишем эти уравнения следующим образом:
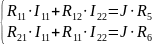
где
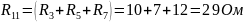 – полное или собственное сопротивление
первого контура;
– полное или собственное сопротивление
первого контура;
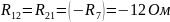 – сопротивление
смежной ветви между первым и вторым
контурами, взятое со знаком минус;
– сопротивление
смежной ветви между первым и вторым
контурами, взятое со знаком минус;
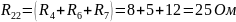 - полное
или собственное сопротивление второго
контура.
- полное
или собственное сопротивление второго
контура.
Подставим значения:
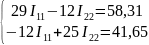
Система уравнений решена методом Крамера относительно искомых токов:
где - главный определитель системы уравнений;
– модифицированный определитель, в котором вместо столбца с номером искомого тока находится столбец правой части уравнений.
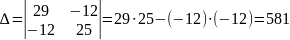
Модифицированный определитель:
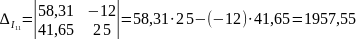
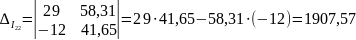
Контурные токи:
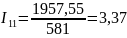 А
А
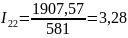 А
А
Токи в цепи относительно контурных токов равны:
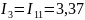 А
А
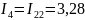 А
А
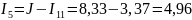 А
А
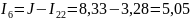 А
А
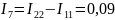 А
А
Баланс мощности в цепи выполняется следующим соотношением:
где
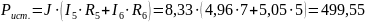 Вт
Вт
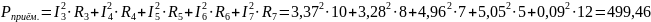 Вт
Вт
Условие выполнено, соответственно, расчёт выполнен верно.

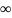
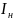 ,
А
,
А