2.13. Расчет электрических цепей при наличии в них магнитно-связанных катушек.

В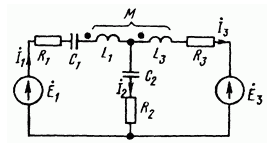 состав электрических цепей могут входить катушки, магнитно-связанные с другими катушками. Поток одной из них пронизывает другую и наводит в них ЭДС взаимоиндукции. При составлении уравнений, для магнитно-связанных цепей необходимо знать согласно или встречно направлены самоиндукции и взаимоиндукции.На электрических схемах сердечник катушки не изображается, одноименные зажимы обозначаются знаками * или ˙.Если на электрической схеме токи двух магнитно-связанных катушек одинаково ориентированы относительно одноименно обозначенных зажимов, то имеет место согласное включение, а в других случаях – встречное.

Составим уравнение по I закону Кирхгофа: .

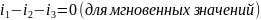По II з. Кирхгофа:;

-для Iконтура:

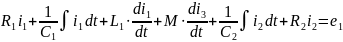
(при встречном включении перед 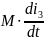ставится (-)).

-для II контура:

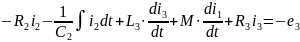
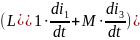- падение напряжений на первой катушке

I з. Кирхгофа в комплексной записи: .

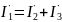II з. Кирхгофа в комплексной форме:

- для Iконтура:

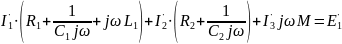
- для II контура:

2.14. Последовательное соединение двух магнитно-связанных катушек.

С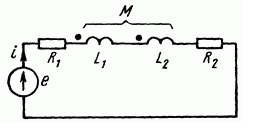 огласное включении двух катушек:

по второму закону Кирхгофа:

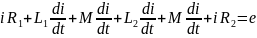
В комплексной форме:

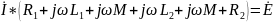
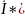
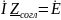
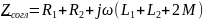
векторная диаграмма

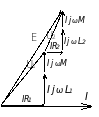
В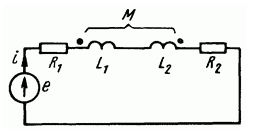 стречное включение двух катушек:

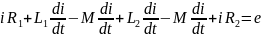
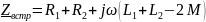
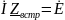
векторная диаграмма:

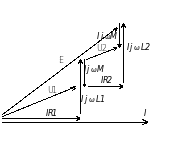
2.15. Определение взаимной индуктивности опытным путем.

П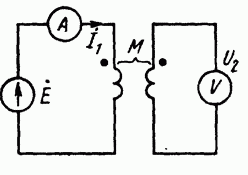 ервый способ:

Проделываем два опыта.

Первый опыт: подключаем катушку последовательно и согласно, измеряем ток, напряжение на входе и активную мощность цепи.

Второй опыт: включаем катушку последовательно и встречно и так же определяем

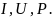
По результатом измерений находим:

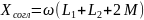
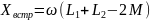
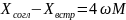
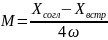
Второй способ:

Подключим первую катушку к источнику синусоидальной ЭДС через амперметр, а к зажимам второй катушки присоединим вольтметр. Измерим ток 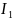и напряжение .

; ;

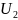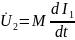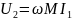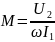
2.16. «Развязывание» магнитно-связанных цепей.

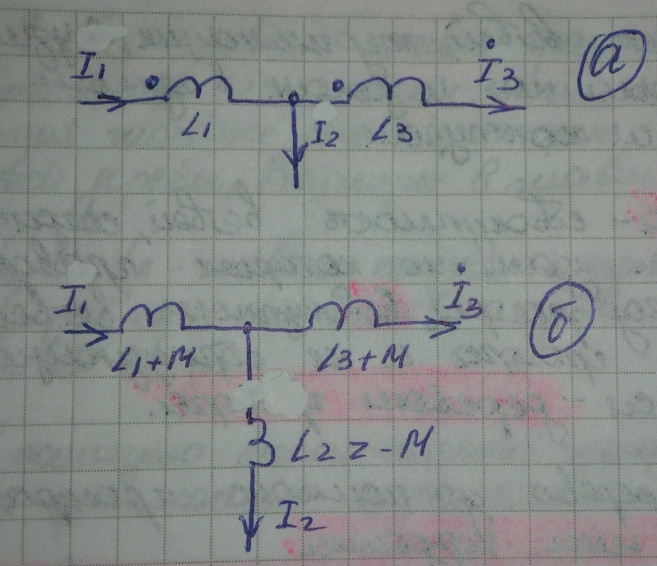
Метод состоит в том, что исходную схему с магнитно-связанными индуктивностями путем введения дополнительных индуктивностей и изменения имевшихся, преобразовывают так, что магнитная связь между всеми индуктивностями в преобразованной схеме будет отсутствовать.

В основе метода лежит неизменность сцепления контура до и после развязывания.

Участок цепи на рис. (а) в расчетном смысле может быть заменен участком, показанном на рис. (б), если катушки будут включены встречно, следует изменить знак перед М.

3. Методы матричного анализа электрических цепей

3.1 Основные понятия о топологии и матрицах электрических цепей.

Методы матричного анализа применяются для моделирования и расчета сложных электрических цепей разветвленной структуры.

Топологический граф электр. цепи – это ее геометрическое представление, при котором ветви ее цепи заменяются линиями (ветвями графа), а узлы цепи – точками(вершинами, узлами графа).

Топологический граф может быть:

• Планарный (если его можно изобразить на плоскости без пересечения ветвей)

• Ориентировочный или направленный (если указаны направления его ветвей)

• Связанный (если существует хотя бы один путь из одного узла в другой)

Подграф – часть графа(ветвь, узел), содержащая с некоторым подмножеством все инцидентные узлы. К подграфам относят: путь, контур, дерево, связи и сечение.

Путь графа – совокупность ветвей, соединяющих два узла.

Замкнутый путь(контур) – путь, начинающий и заканчивающий в 1-м узле.

Сечение топологического графа – совокупность ветвей, удаление которых приводит к распаду графа на подграфы.

Дерево графа - совокупность ветвей, соединяющих все узлы графа и не образующих при этом контур.

Хорды(ветви связи) – ветви, дополняющие дерево до полного графа.

Главное сечение графа – сечение, в состав которого входит лишь одна ветвь дерева, а остальные - хорды.

Граф, имеющий pветвей и q узлов содержит: m=q-1ветвей дерева, n=p-q+1 ветвей связи.

Ветви с источниками напряжения включают в ветви дерева.

Главный контур – контур, в состав которого входит лишь одна хорда. Добавление главной ветви к дереву дает главный контур. Т.е. число главных контуров равно числу главных ветвей или ветвей связи.Главный контур ориентируют.Его ориентация совпадает с ориентацией главной ветви. Главные контура нумеруют. Главные контура отличаются друг от друга хотя бы одной (главной) ветвью. Такие контура являются независимыми.

С помощью топологического графа формируют матрицы в электрические цепи, которые представляют собой ее численную модель, геом.(топологический) свойства цепи не зависят от элементов цепи.

Основные топологические матрицы:

1. Узловая матрица (матрица соединений А). Полнаяузловая матрица А_с – это матрица, в которой число столбцов равно числу ветвей графа p, а число строк равно числу узлов q. Номера строк совпадают с номерами узлов, а номера столбцов - с номерами ветвей графа.

Для получения из полной матрицы А_с вычеркивают любую строку, обычно соответствующую нулевому узлу.

Правила заполнения матрицы:

• «1» – если ветвь присоединена к узлу и имеет направление от узла топологического графа

• «-1» - если ветвь входит в узел

• «0» - если ветвь не присоединена к узлу графа

2. Матрица главных сечений Q – это таблица коэффициентов уравнений, составленных по 1-му закону Кирхгофа для сечений, где строки матрицы соответствуют сечениям, а столбцы – ветвям.

Правила заполнения матрицы:

• «1» – если ветвь входит в состав сечения и ее направление совпадает с направлением главного сечения

• «-1» - если ветвь входит в состав сечения, но ее направление не совпадает с направлением главного сечения

• «0» - если ветвь не входит в состав сечения

При таком способе заполнения матрицы в ее левой части формируется единичная подматрица Е, а в правой подматрица F.

3. Матрица главных контуров В (контурная матрица) - таблица, в которой число строк равно числу контуров, число столбцов – числу ветвей графа. Номера столбцов совпадают с номерами ветвей, а номера строк с номерами главных контуров.

Правила заполнения матрицы:

• «1» – если ветвь входит в контур и ее направление совпадает с направлением контура

• «-1» - если ветвь входит в контур, но ее направление не совпадает с направлением контура

• «0» - если ветвь не входит в контур

Число главных контуров равно числу ветвей связи.

4. Диагональная матрица сопротивлений, столбцовые матрицы (напряжений, токов, ЭДС)