- •Линейные электрические цепи постоянного тока
- •1.1. Электрическая цепь и её элементы. Схемы электрических цепей.
- •1 .2. Закон Ома для участка цепи с пассивными элементами.
- •1.3. Закон Ома для участка цепи с пассивными элементами, содержащего эдс.
- •1. 4.Топологические понятия в электротехнике.
- •1.5. Законы Кирxгоффа.
- •6 . Анализ цепей с одним источником при последовательном, параллельном и смешанном соединении приемников.
- •7. Метод эквивалентных преобразований.
- •8.Метод эквивалентного преобразования соединения пассивных элементов «звездой» и «треугольником».
- •9 . Метод непосредственного применения законов Кирхгофа.
- •10.Расчет сложных цепей методом контурных токов.
- •11 Метод межузлового напряжения
- •1 2 Метод эквивалентного генератора
- •14.Баланс мощности.
- •1.15. Мощность потерь и кпд
- •1.16.Активный и пассивный двухполюсник.
- •1.17. Передача энергии от активного двухполюсника к нагрузке.
- •2.1 Принцип получения переменной эдс, напряжения, тока. Параметры. Характеризующие синусоидальные функции времени
- •2.2 Действующее и среднее значения переменного тока, напряжения, эдс.
- •2.3 Изображение синусоидальных функций времени вращающимися векторами. Векторные диаграммы.
- •2.4 Представление синусоидальных эдс, напряжений и токов комплексными числами
- •2.5 Резистивный элемент в цепи переменного тока.
- •2.6 Идеальная катушка в цепи переменного тока.
- •2.7 Идеальный конденсатор в цепи переменного тока
- •2.8 Цепь переменного тока, содержащая последовательно соединенные резистивный элемент, индуктивную катушку и конденсатор.
- •2.9. Активная и реактивная составляющие тока. Проводимость в цепях переменного тока.
- •2.10. Расчет цепей переменного тока комплексным методом.
- •2.11. Мощность в цепях переменного тока.
- •Технико-экономическое значение повышения коэффициента мощности и способы компенсации реактивной мощности.
- •2.13. Расчет электрических цепей при наличии в них магнитно-связанных катушек.
- •2.14. Последовательное соединение двух магнитно-связанных катушек.
- •2.15. Определение взаимной индуктивности опытным путем.
- •2.16. «Развязывание» магнитно-связанных цепей.
- •3. Методы матричного анализа электрических цепей
- •3.1 Основные понятия о топологии и матрицах электрических цепей.
- •3.2 Метод ветвей дерева и хорд.
- •3.3. Метод контурного анализа в матричной форме.
- •3.4. Метод узлового анализа в матричной форме.
- •Электрические трехфазные цепи.
- •5. Понятие о трехфазной системе электрических цепей.
- •6.Получение трехфазной системы э.Д.С.
- •7.Соединение обмоток генератора и фаз приемника звездой.
- •8.Соединение обмоток генератора и фаз приемника треугольником.
- •9.Напряжение между нейтральными точками генератора и приемника.
- •10.Мощность трехфазной системы.
- •11.Соотношение между линейными и фазовыми напряжениями и токами.
- •12.Преимущества трехфазных систем.
- •13.Расчет трехфазных цепей.
- •14 Оператор а трехфазной системы
- •15.Активная, реактивная и полная мощность трехфазной системы.
- •16.Измерение активной мощности в трехфазной системе
2.7 Идеальный конденсатор в цепи переменного тока

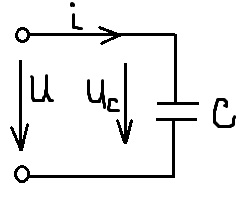

Конденсатор будет периодически перезаряжаться, что обусловит протекание через него зарядного тока (I), пропорционального скорости изменения заряда.
 ;
;


 имеет
размерность сопротивления(Ом) и называется
емкостным сопротивлением.
имеет
размерность сопротивления(Ом) и называется
емкостным сопротивлением.
Т
 ок
через конденсатор опережает по фазе
напряжение на конденсаторе на угол 90
градусов.
ок
через конденсатор опережает по фазе
напряжение на конденсаторе на угол 90
градусов.
 ,
– реактивная мощность.
,
– реактивная мощность.
2.8 Цепь переменного тока, содержащая последовательно соединенные резистивный элемент, индуктивную катушку и конденсатор.

Напряжения на индуктивности емкости сдвинуты относительно друг друга на 180°, их алгебраическая сумма называется реактивным напряжением.


 =
=
 -амплитуда
реактивного напряжения.
-амплитуда
реактивного напряжения.
знак
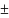 зависит от соотношения величин напряжений
на индуктивности и емкость.
зависит от соотношения величин напряжений
на индуктивности и емкость.

а) -
цепь имеет активно-индуктивный
характер.Напряжение на зажимах цепи
опережает по фазе ток на угол фи.UrиU
образуют треугольник напряжения.
-
цепь имеет активно-индуктивный
характер.Напряжение на зажимах цепи
опережает по фазе ток на угол фи.UrиU
образуют треугольник напряжения.



мощности:
активная:

реактивная:

полная:

b
б)



в)
При
равенстве реактивных сопротивлений,
индуктивности, емкости, будут равны
падения напряжений
 ,
в этом случае напряжения на зажимах
цепи совпадают по фазе с током и цепь
имеет активный характер.
,
в этом случае напряжения на зажимах
цепи совпадают по фазе с током и цепь
имеет активный характер.

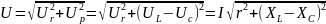
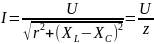
закон Ома для цепи синусоидального тока с последовательным соединением активного сопротивления.



2.9. Активная и реактивная составляющие тока. Проводимость в цепях переменного тока.
Множитель
 представляет собой комплекс, имеет
размерность сопротивления и обозначается
числом
представляет собой комплекс, имеет
размерность сопротивления и обозначается
числом
 Его называют комплексным сопротивлением:
Его называют комплексным сопротивлением:

Как
и всякий комплекс,
 можно записать в показательной форме.
Модуль комплексного сопротивления
принято обозначать через
можно записать в показательной форме.
Модуль комплексного сопротивления
принято обозначать через
 Точку над
Точку над
 не ставят, потому что принято ставить
ее только над такими комплексными
величинами, которые отображают
синусоидальные функции времени.
не ставят, потому что принято ставить
ее только над такими комплексными
величинами, которые отображают
синусоидальные функции времени.
В
общем случае
имеет некоторую действительную часть
 и некоторую мнимую часть
и некоторую мнимую часть


где
– активное сопротивление;
 – реактивное сопротивление.
– реактивное сопротивление.
Под
комплексной проводимостью
 понимают величину, обратную комплексному
сопротивлению
:
понимают величину, обратную комплексному
сопротивлению
: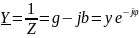
Единица
комплексной проводимости – См (Ом-1).
Действительную часть ее обозначают
через
 ,
а мнимую – через
,
а мнимую – через
 .
. ;
;
 ;
;
 .
.
При использовании комплексной проводимости закон Ома записывают так:

где
 – активная составляющая тока;
– активная составляющая тока; – реактивная составляющая тока;
– реактивная составляющая тока;
 – напряжение на участке цепи, сопротивление
которого равно
.
– напряжение на участке цепи, сопротивление
которого равно
.
Полная проводимость и ее составляющие образуют треугольник проводимости:



В зависимости от соотношения индуктивности и емкости проводимость ветвей меняется знак угла сдвига фаз между током и напряжением на входе цепи.
В связи с этим возможно 3 случая:
Ток отстает по фазе от напряжения. Цепь имеет активно-индуктивный характер.
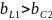
I опережает по фазе U. Цепь имеет активно-емкостной характер.

Ток и напряжение на входе цепи совпадают по фазе. Это свидетельство о чисто активном характере нагрузки.