
2
.docxF = x1+3x2 → max,
-2x1+x2≤0, (1)
x1+2x2≤10, (2)
x1+x2≥3, (3)
x1-x2≤5, (4)
x1≤6, (5)
x1 ≥ 0, (6)
x2 ≥ 0, (7)
Побудуємо область допустимих рішень
1
х |
у |
0 |
0 |
1 |
2 |
2
х |
у |
0 |
5 |
10 |
0 |
3
х |
у |
0 |
3 |
3 |
0 |
4
х |
у |
5 |
0 |
0 |
-5 |
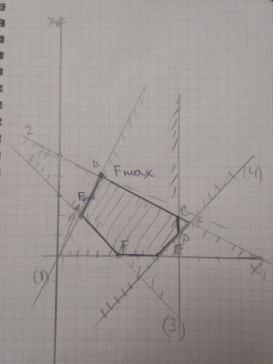
Вектор-градієнт,
складений з коефіцієнтів цільової
функції, вказує напрямок максимізації
F (X). Початок вектора - точка (0; 0), кінець
- точка (1; 3). Будемо рухати цю пряму
паралельним чином. Оскільки нас цікавить
максимальне рішення, тому рухаємо пряму
до останнього торкання позначеної
області. На графіку ця пряма позначена
пунктирною лінією. Пряма
F (x) = const перетинає область в точці B. Так
як точка B отримана в результаті перетину
прямих (1) і (2), то її координати задовольняють
рівнянням цих прямих:
-2x1+x2=0
Пряма
F (x) = const перетинає область в точці B. Так
як точка B отримана в результаті перетину
прямих (1) і (2), то її координати задовольняють
рівнянням цих прямих:
-2x1+x2=0
x1+2x2=10
Вирішивши систему рівнянь, отримаємо: x1 = 2, x2 = 4
Звідки знайдемо максимальне значення цільової функції:F(X) = 1*2 + 3*4 = 14
