
доп.завд
.docx
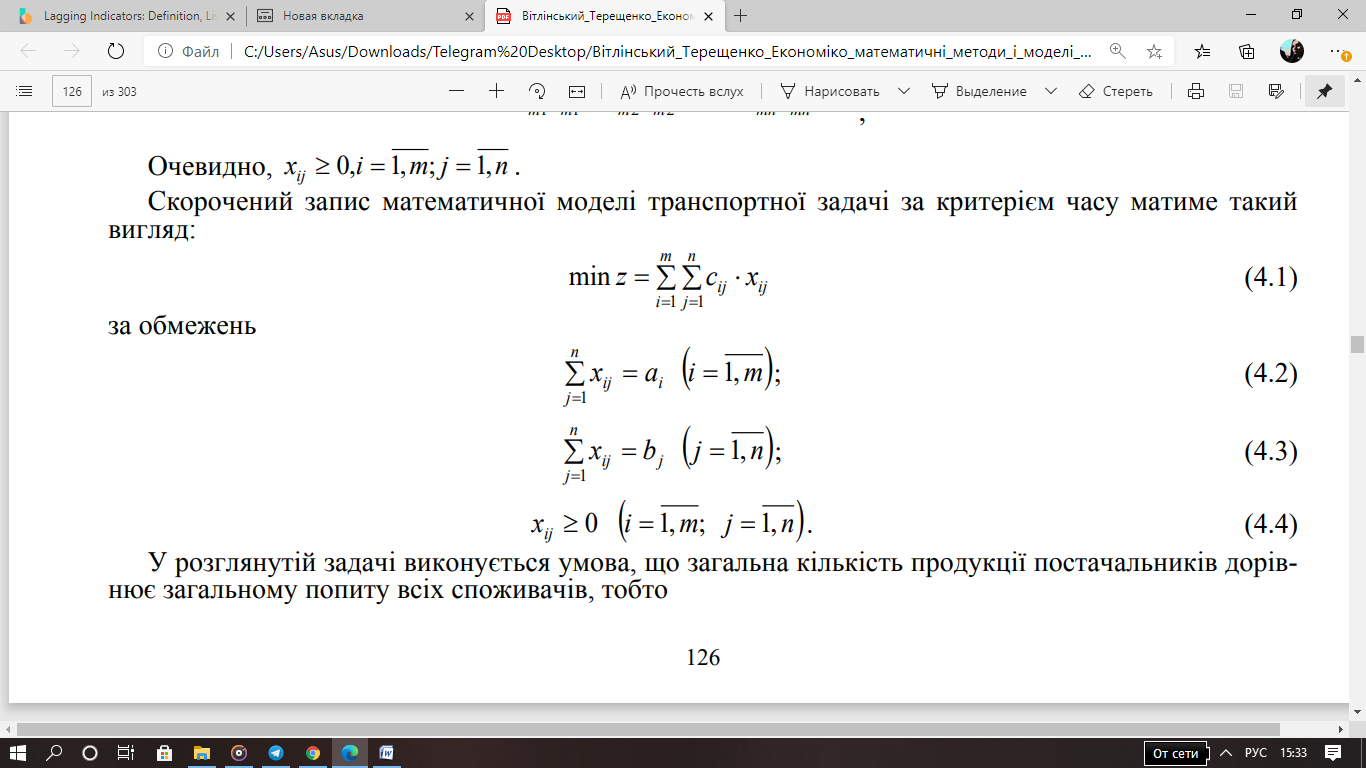
Доведення теореми 2 (умови існування розв’язку транспортної задачі)
Необхідною і достатньою умовою існування розв’язку транспортної задачі є її збалансованість:

Доведення.
Необхідність. Нехай задача має розв’язок![]() ,
тоді для нього виконуються
,
тоді для нього виконуються
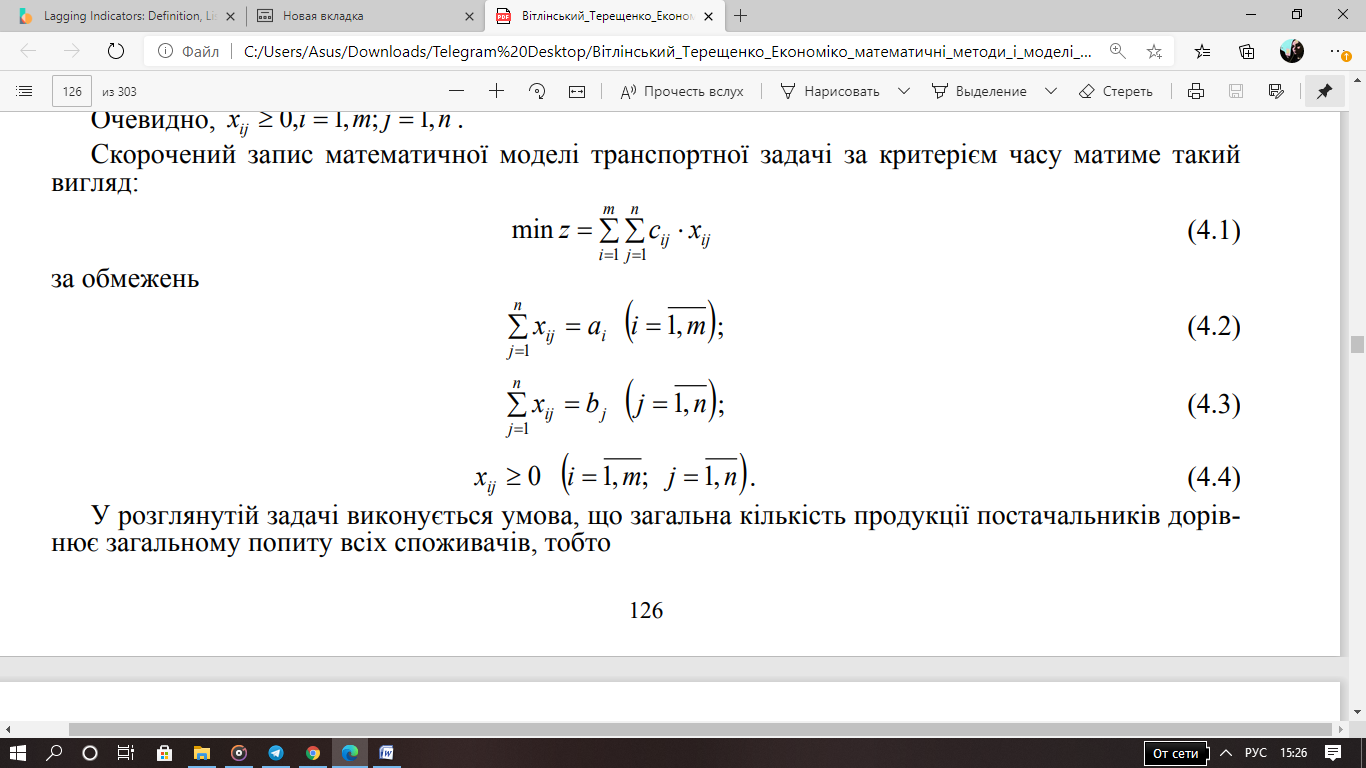 .
.
Просумуємо ліві та праві частини і матимемо
Оскільки праві частини рівнянь збігаються, то збігатимуться також і ліві, отже, виконується умова

Достатність. Потрібно показати, що при заданій умові існує хоча б один план задачі і цільова функція на множині планів обмежена.
Нехай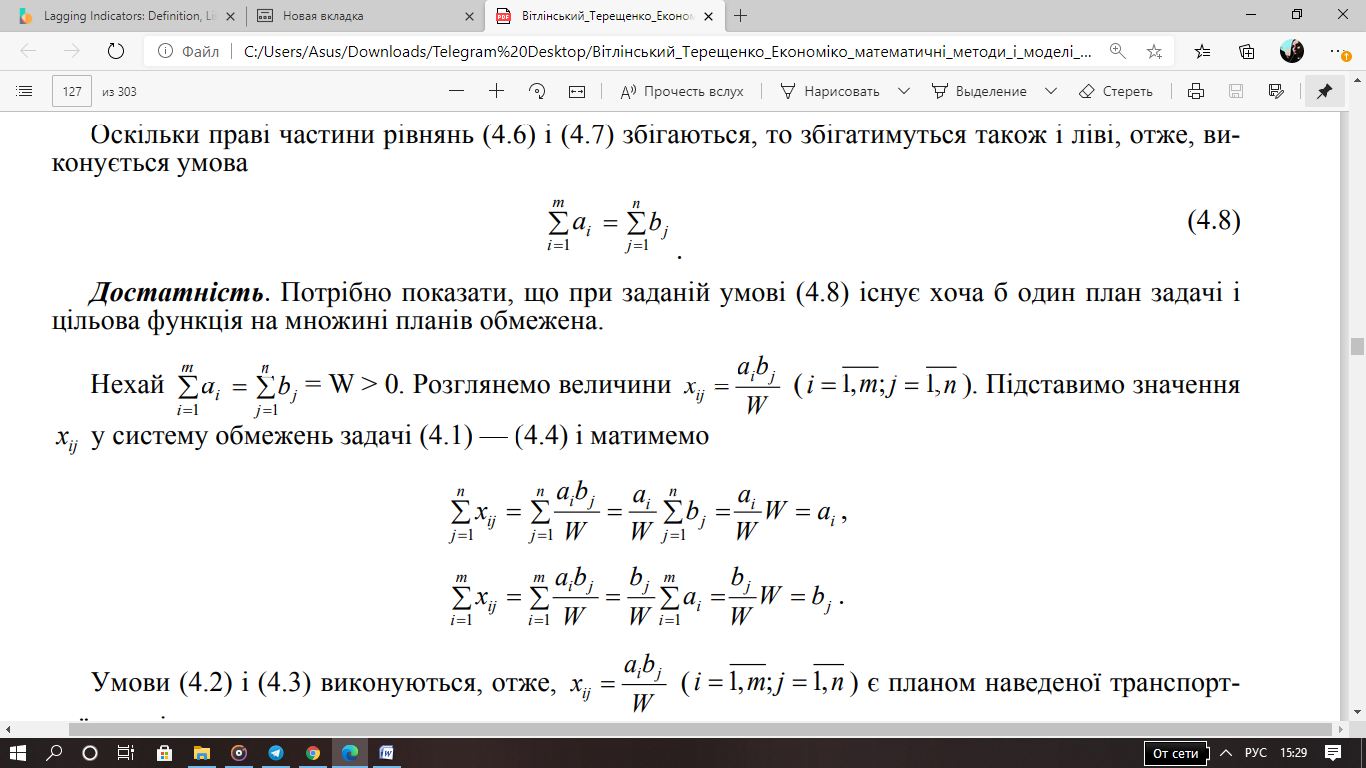 .
Розглянемо величини
.
Підставимо значення ij x у систему обмежень
задачі і матимемо
.
Розглянемо величини
.
Підставимо значення ij x у систему обмежень
задачі і матимемо
Умови
виконуються, отже,
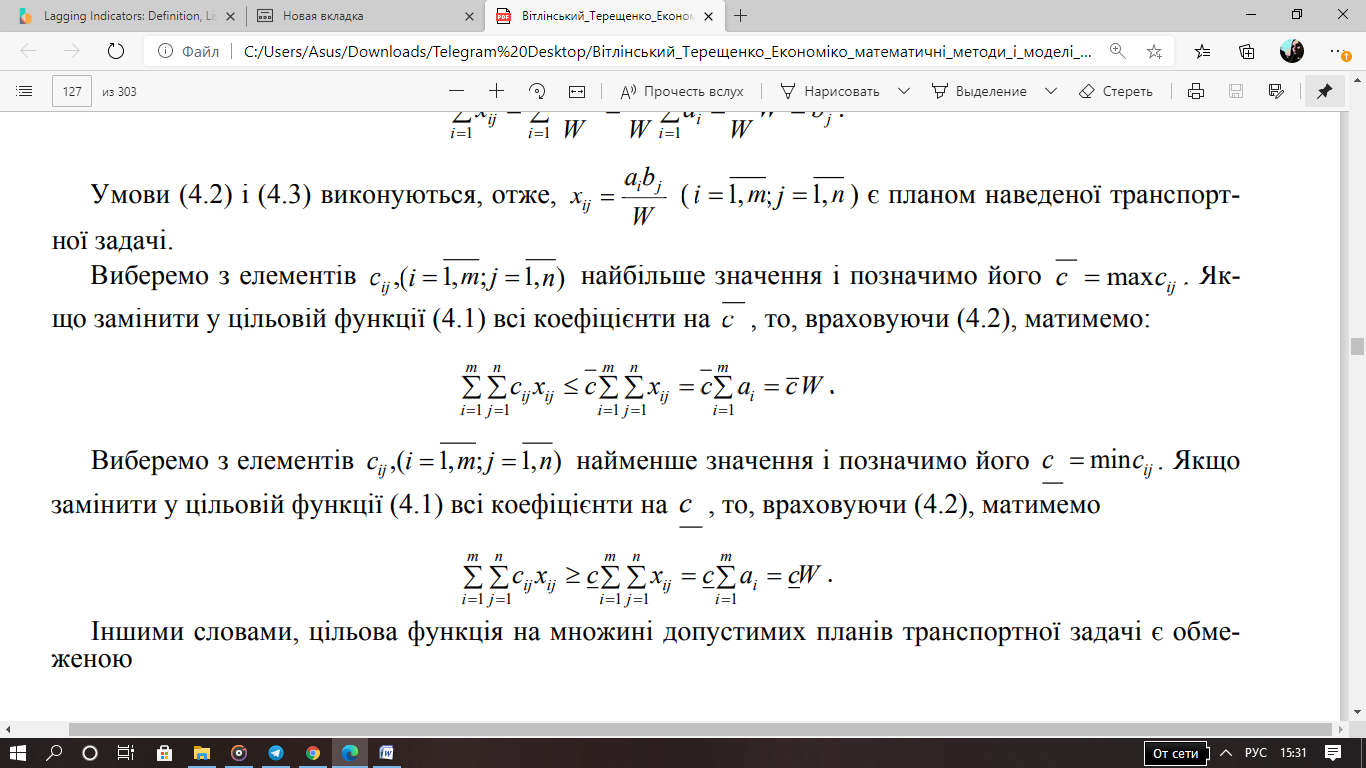 є
планом наведеної транспортної задачі.
є
планом наведеної транспортної задачі.
Виберемо
з елементів
найбільше
значення і позначимо його ij c = maxc . Якщо
замінити у цільовій функції
 всі коефіцієнти на c , то, враховуючи
,
матимемо
всі коефіцієнти на c , то, враховуючи
,
матимемо
Виберемо
з елементів
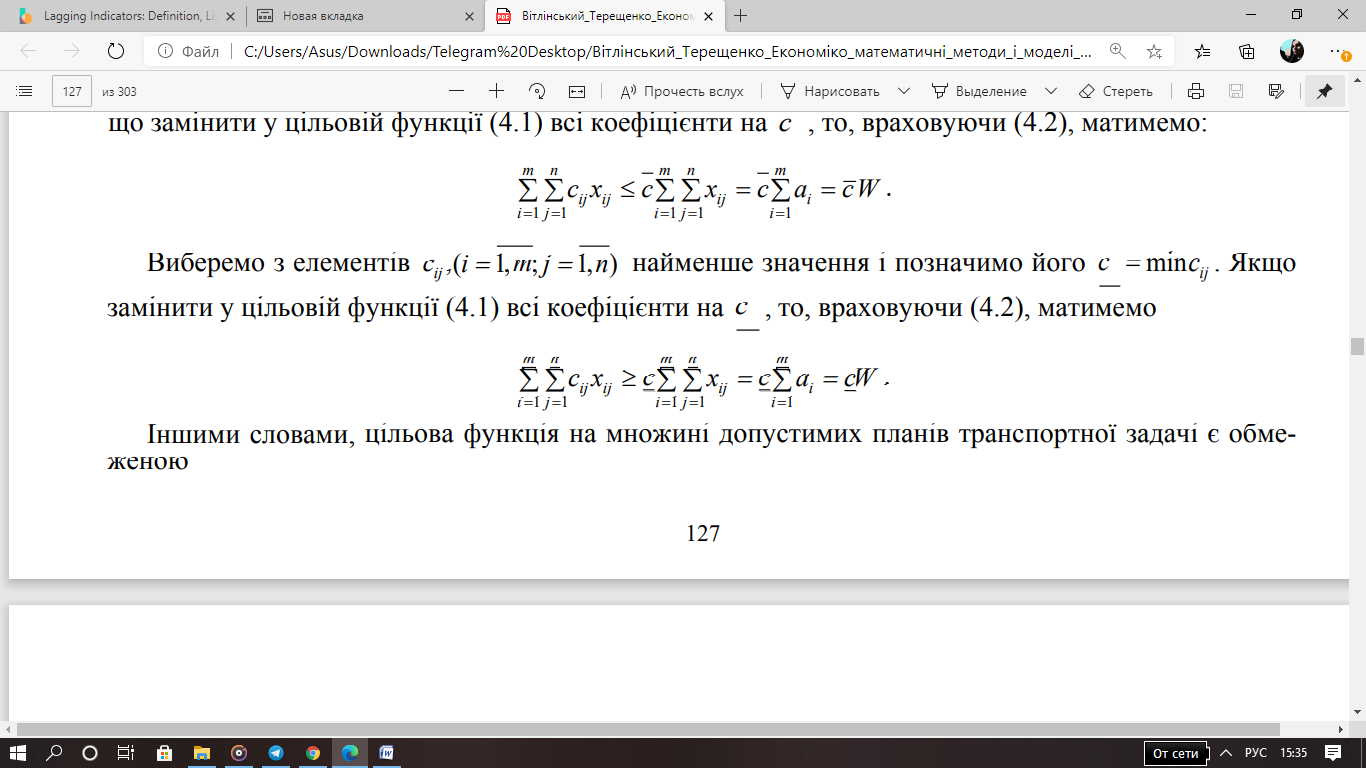 найменше
значення і позначимо його ij c = minc .
найменше
значення і позначимо його ij c = minc .
Якщо замінити у цільовій функції всі коефіцієнти на c , то, враховуючи , матимемо:
Іншими словами, цільова функція на множині допустимих планів транспортної задачі є обмеженою

Теорему доведено.
