МО Практ 2 Симплекс алгоритм

Практическое занятие №2 (Методы оптимизации)

Симплекс алгоритм задачи линейного программирования

Симплекс метод используется для решения задач, записанных в канонической форме:

(1)

(2)

Система (1) это система линейных уравнений.

(x1,x2,…,xn) – допустимое решение задачи, если оно одновременно удовлетворяет условиям (1) и (2), т.е. является решением системы (1) и все его параметры неотрицательные. Таким образом, если допустимые решения задачи существуют, то система (1) имеет решение. Если же система (1) не имеет решения, то допустимых решений задачи нет. Однако, если система (1) имеет решения, то отсюда не следует, что у задачи есть допустимые решения, ибо они еще должны удовлетворять условием (2). Такие примеры позже будут рассмотрены.

Для того чтобы найти оптимальное решение задачи необходимо вначале убедиться, что есть допустимые решения, иначе не из чего искать наилучшее. А для того чтобы были допустимые решения, необходимо, чтобы система (1) имела решения. Поэтому нужно уметь определять если у системы (1) решения, а если есть, то находить эти решения. Кстати, если система (1) не имеет решений, то нет и допустимых и, следовательно, нет оптимального решения задачи.

Система линейных уравнений, которая имеет решения, называется совместной. Кстати, совместная система линейных уравнений, имеет либо одно решение, либо бесконечно много. Других вариантов нет.

Пусть матрица =A это матрица, состоящая из коэффициентов система линейных уравнений (1). Тогда расширенная матрица =(A | B) это матрица, состоящая из коэффициентов система линейных уравнений (1), т.е. матрица А, в которую добавили еще один столбец из значений, стоящих в правой части линейных уравнений (1).

В линейной алгебре есть такое понятие ранг матрицы, обозначаемое как rang(матрица) и представляющее собой целое число. Пусть rang(A)=r₁ и rang(A|B)=r₂ . Из линейной алгебры известно, что, если в матрицу добавить столбец, то ранг может либо увеличится, либо остаться без изменений, т.е. r₁ r_2. . Там же доказывается утверждение, что

Система совместна, если r₁=r₂.

Теперь научимся вычислять эти ранги матриц. Продемонстрируем на конкретном примере.

Пример 1.

,

Используя метод Гаусса-Жордана, преобразуем матрицу. Вычитаем из каждой строки, начиная со второй первую строку или первую строку, умноженную на число, так чтобы в первой колонке остались нули ниже первой строки. Далее переходим ко второй строке. Вычитаем из каждой строки, начиная с третьей вторую строку или вторую строку, умноженную на число, так чтобы во второй колонке остались нули . ниже второй строки. И так далее до тех пор пока вы не дойдете до строки, соответствующей последней колонке до вертикальной черты или доходите до строки, состоящую из нулей до вертикальной черты и все строки ниже нее состоят из нулей до вертикальной черты. Число, получившихся ненулевых строк среди строк до вертикальной черты есть ранг матрицы. Число, получившихся ненулевых строк среди всех строк есть ранг расширенной матрицы.

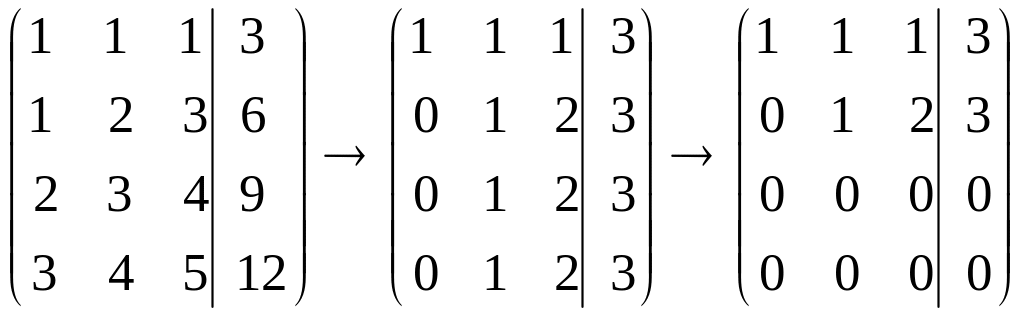
A = r₁=rang(A)=2

(A|B) = r₂=rang(A|B)=2

r₁= r₂, следовательно система совместна

Там же в линейной алгебре доказывается утверждение, что

Если r₁< r₂, то система несовместна:

Пример 2.

A = r₁=rang(A)=2

(A|B) = r₂=rang(A|B)=3

r₁< r₂, следовательно система несовместна, т.е. система уравнений примера 2 не имеет решений.

Пример 3. (Пример, когда нет допустимых решений, хотя система имеет решения)

Целевая функция имеет вид:

Z= x₁ - x₂ max

Уравнение x₁ + x₂ = -1 имеет бесконечное число решений. Но среди них либо x₁<0, либо x₂<0, так как два неотрицательных числа в сумме не могут равняться отрицательному. Отсюда следует, что допустимых решений нет, ибо допустимые решения – это неотрицательные решения. Итак, это пример ситуации, когда система линейных уравнений (1) имеет бесконечное число решений, но среди них нет ни одного, удовлетворяющих условию (2), условию неотрицательности решения.

Зависимые (базисные) переменные – это переменные, входящие только в одно из уравнений с коэффициентом 1, а во все остальные с коэффициентом 0. Они выражаются через свободные переменные.

Число базисных переменных равно r.

Число свободных переменных равно n-r.

Пример 4.

r=r₁=r₂=2

Запишем полученную систему уравнений:

Выразим базисные переменные (x₁ и x₂) через свободные:

Базисное решение: свободные переменные обнуляются: x₃= 0, x₄= 0,

тогда x₁= -2 и x₂= 6.

Базисная переменная x₁ оказалась отрицательна, что противоречит условию, наложенному на все переменные ( ). Следовательно, решение является не допустимым.

Запишем полученную систему уравнений:

Выразим базисные переменные (x₂ и x₃) через свободные:

Базисное решение: свободные переменные обнуляются: x₁= 0, x₄= 0,

тогда x₂= 2 и x₃= 2.

Все переменные удовлетворяют условию , следовательно, базисное решение является допустимым. Область допустимых решений не пуста, так как существует допустимое решение.

Количество возможных базисных решений ,

в общем случае

Симплекс алгоритм

Рассмотрим пример:

Пример 1:

Целевая функция Z=x₁ + x₂ - x₃ min

Используя метод Гаусса-Жордана преобразуем матрицу так, чтобы базисные переменные можно было выразить через свободные.

Пусть базисные переменные: x₁, x₂; свободные переменные: x₃, x₄;

Ранг матрицы: r=r₁=r₂=2

Число базисных переменных равно 2.

Число свободных переменных равно 2.

Запишем полученную систему уравнений:

Выразим базисные переменные через свободные:

Базисное решение: свободные переменные обнуляются: x₃= 0, x₄= 0,

тогда x₁= и x₂= - допустимое базисное решение.

В общем случае , где Z₀ – решение в базисных переменных,

x_k – свободные переменные, С_k – коэффициенты при свободных переменных.

Вычисляем значение целевой функции :

Z₀=

Проверим решение на оптимальность. Для этого выразим целевую функцию через свободные переменные:

Z=x₁ + x₂ - x₃=

Если все коэффициенты неотрицательны, то решение оптимально, причем если хотя бы один коэффициент равен 0, то решение не единственно (их бесконечно много), иначе решение единственное.

Если хотя бы один коэффициент отрицательный, то решение не оптимально.

В нашем примере коэффициент перед свободной переменной x₃ отрицательный, следовательно, решение не оптимально.

Увеличим переменную x₃, т.е. x₃> 0 при x₄=0 .

Посмотрим, как базисные переменные зависят от x₃:

Заметим что, увеличив переменную x₃ до , базисная переменная x₂ обнуляется.

Пусть базисные переменные: x₁, x₃; свободные переменные: x₂, x₄.Выразим нововведенную базисную переменную через свободные:

Тогда

Базисное решение: свободные переменные обнуляются: x₂= 0, x₄= 0,

тогда x₁= 3 и x₃= - допустимое базисное решение.

Вычисляем значение целевой функции:

Z=

Выразим целевую функцию через свободные переменные:

Z=

Коэффициенты при свободных переменных положительные, т.е. решение оптимальное и единственное.

Единственное оптимальное решение:

Z*= ; x*₁=3; x*₂=0; x*₃= ; x*₄=0;

Пример 2:

Целевая функция имеет вид: Z=x₄-x₅ min

Заметим, что переменные x₁, x₂, x₃ входят только в одно из уравнений с коэффициентом 1, а во все остальные - с коэффициентом 0. Возьмем их в качестве базисных и выразим через оставшиеся переменные:

Найдем начальное базисное решение: х₄ = x₅ =0; тогда x₁=1, x₂=2, x₃=3.

Вычислим значение функции: Z= x₄-x₅=0.

Увеличим переменную x₅.

Посмотрим, как базисные переменные зависят от x₅:

Базисные переменные: x₁, x₃, x₅; свободные переменные: x₂, x₄.Выразим нововведенную базисную переменную через свободные:

Найдем базисное решение: х₂ = x₄ =0; тогда x₁=5, x₃=1, x₅=2, Z₀=-2

Выразим функцию через свободные переменные:

Z= x₄-x₅= x₄-2+ x₂- 2x₄= -2+ x₂- x₄.

Увеличим переменную x₄, x₂=0, тогда:

Базисные переменные: x₁, x₄, x₅; свободные переменные: x₂, x₃.Выразим нововведенную базисную переменную через свободные:

Найдем базисное решение: х₂ = x₃ =0; тогда x₁= , x₄= , x₅= , Z₀=-

Выразим функцию через свободные переменные:

Z= x₄-x₅= =

Решение оптимальное и единственное:

Z*= ; x*₁= ; x*₂=0; x*₃=0; x*₄= ; x*₅= ;

Пример 3. (Пример задачи в общей постановке)

Целевая функция Z=3x₁+x₂ max

Запишем задачу в канонической форме. Для этого в каждом неравенстве добавим дополнительную переменную, чтобы уровнять обе стороны неравенства, а в качестве целевой функции будем считать Z’= -Z:

Таким образом, получаем целевую функцию Z’=-3x₁-x₂ min и систему уравнений:

В качестве базисных переменных возьмем добавленные переменные и выразим их через остальные:

Найдем базисное решение: х₁ = x₂ =0; тогда x₃= 6, x₄= 8, x₅= 2, Z’₀=0

Выразим функцию через свободные переменные: Z’=-3x₁-2x₂

Увеличим х₁, х₂=0, тогда:

Базисные переменные х₁, х₃, х₅; свободные переменные х₂, х₄:

Найдем базисное решение: х₂ = x₄ =0; тогда x₁= 4, x₃= 2, x₅= 2, Z’₀= -12

Выразим функцию через свободные переменные:

Z’=-3x₁-2x₂= =

Увеличим х₂, х₄=0, тогда:

Базисные переменные х₁, х₂, х₅; свободные переменные х₃, х₄:

Найдем базисное решение: х₃ = x₄ =0; тогда x₁= , x₂= , x₅= , Z’₀= -10 - =-12

Выразим функцию через свободные переменные функции:

Z’= =

Оптимальное решение для вспомогательной задачи:

(Z’)*=-12 ; x*=( , ,0,0, )

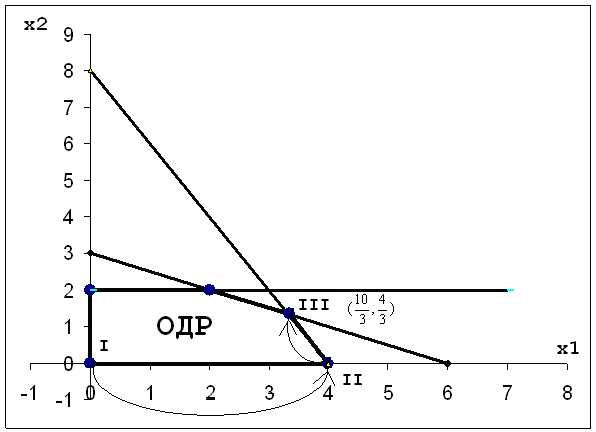
Выпишем решение задачи для исходной задачи:

Z*= -(Z’)*= 12 ; x*=( , )

Заметим, что каждое допустимое базисное решение соответствует вершине многоугольника ОДР в графическом методе. Переход к другому базисному решению в симплекс алгоритме соответствует переходу в соседнюю вершину многоугольника ОДР в графическом методе.

Контрольные вопросы

1. Каноническая форма задачи ЛП.

2. Что означает совместная система линейных уравнений.

3. Сколько решений может быть у системы линейных уравнений.

4. Сколько решений может быть у совместной системы линейных уравнений.

5. Как совместность системы линейных уравнений связана с рангом.

6. Что такое допустимое решение канонической задачи ЛП.

7. Каким условиям должно удовлетворять допустимое решение канонической задачи ЛП.

8. Что такое базисное решение.

9. Что такое допустимое базисное решение.

10. Что такое недопустимое базисное решение.

11. Чему соответствует допустимое базисное решение в геометрическом представлении ОДР.

12. В чем суть симплекс алгоритма.

13. Как определяется отсутствие допустимых решений.

14. Как определяется оптимальность допустимого решения.

15. Как определяется единственность оптимального решения.

16. Как определяется множественность оптимальных решений.