
- •Расчетные задания на тестирование
- •Метод перебора.
- •Метод перебора.
- •1. Математическая постановка задачи оптимизации.
- •2. Понятие о численных методах оптимизации. Методы поиска нулевого, первого и второго порядков. Пассивные и активные (последовательные) методы поиска.
- •3. Конечно шаговые и бесконечно шаговые методы поиска. Сходимость методов. Условия останова методов поиска.
- •4. Теорема существования решения оптимизационной задачи.
- •7. Необходимые условия экстремума первого порядка (гладкие функции многих переменных).
- •9.Пассивные методы поиска экстремума.
- •10.Метод перебора.
- •11. Алгоритм оптимального пассивного поиска.
- •12.Теорема об оптимальности пассивного поиска.
- •14. Метод поразрядного поиска.
- •15. Метод дихотомий
- •16. Метод деления отрезка пополам
- •17. Метод золотого сечения
- •20. Метод средней точки
- •26 Метод симплекса.
- •27 Метод циклического покоординатного спуска.
- •29 Градиентные методы
- •30 Градиентный метод с постоянным шагом.
- •31 Градиентный метод с дроблением шага.
- •Метод наискорейшего спуска
- •Методы покоординатного спуска
- •Метод покоординатного спуска с постоянным шагом
- •Метод покоординатного спуска с дроблением шага
- •Метод Гаусса-Зейделя
- •Постановка задач линейного программирования
- •Способы перехода от одной формы задачи лп к другой
- •Базисное решение задачи лп Симплексный метод решения задач линейного программирования
- •Графический метод решения задачи лп
- •Симплекс-метод решения задачи лп
- •Метод искусственных переменных
Метод покоординатного спуска с постоянным шагом
Схема алгоритма покоординатного спуска с постоянным шагом
Шаг 1.
При к = 0 вводятся исходные данные х0, ε1, α .
Шаг 2.
![]() Осуществляется
циклический по j (j=1,2,…,n) покоординатный
спуск из точки хkn
по
формуле:
Осуществляется
циклический по j (j=1,2,…,n) покоординатный
спуск из точки хkn
по
формуле:
Шаг 3.
![]() Если
||x(k+1)n–xkn||1,
то поиск минимума заканчивается, причем:
Если
||x(k+1)n–xkn||1,
то поиск минимума заканчивается, причем:
Иначе к=к+1 и переходим к шагу 2.
![]() Если
же шаг
выбирается
из условия минимума функции:
Если
же шаг
выбирается
из условия минимума функции:
то мы получаем аналог метода наискорейшего спуска, называемый обычно методом Гаусса – Зейделя.
____________________Вопрос 35____________________
Метод покоординатного спуска с дроблением шага
____________________Вопрос 36____________________
Метод Гаусса-Зейделя
Схема метода Гаусса – Зейделя
Шаг 1.
При к=0 вводятся исходные данные х0,1.
Шаг 2.
![]() Осуществляется
циклический по j (j=1,2,…,n) покоординатный
спуск из точки хkn
по формулам:
Осуществляется
циклический по j (j=1,2,…,n) покоординатный
спуск из точки хkn
по формулам:
![]() где
kn+j-1 является
решением задачи одномерной минимизации
функции:
где
kn+j-1 является
решением задачи одномерной минимизации
функции:
Шаг 3.
![]() Если
||x(k+1)n–xkn||1,
то поиск минимума заканчивается, причем:
Если
||x(k+1)n–xkn||1,
то поиск минимума заканчивается, причем:
Иначе к = к + 1 и переходим к шагу 2.
____________________Вопрос 37____________________
Постановка задач линейного программирования
Математически задача линейного программирования (ЗЛП) заключается в нахождении наибольшего или наименьшего значения линейной функции многих переменных при линейных ограничениях типа равенств и неравенств, когда на переменные есть или нет ограничений на знак.
В общем случае математическая постановка задачи линейного программирования может быть записана в виде:
(1)
![]()
(2)
![]() ,
,![]()
(3)
![]() ,
,![]() ,
(1.1)
,
(1.1)
(4)
![]() ,
,![]() .
.
Здесь
![]() — целевая
функция, линейная относительно своих
аргументов,
— целевая
функция, линейная относительно своих
аргументов,
![]() —
число переменных,
—
число переменных,![]() —
число ограничений задачи. Условия (2),
(3) задают линейные ограничения на ресурсы
в виде неравенств и равенств, условия
(4) определяют ограничения на знак
переменных.
—
число ограничений задачи. Условия (2),
(3) задают линейные ограничения на ресурсы
в виде неравенств и равенств, условия
(4) определяют ограничения на знак
переменных.
Целевая функция
![]() ,
где
,
где
![]() выражает критерий оптимизации, отражающий
основную цель преследуемую субъектом
управления — повышение эффективности
использования ресурсов. В производственной
сфере показателями эффективности
являются обычно выручка или прибыль,
что приводит к задачам максимизации.
Именно (1.1) представляет собой формулировку
задачи максимизации целевой функции.
выражает критерий оптимизации, отражающий
основную цель преследуемую субъектом
управления — повышение эффективности
использования ресурсов. В производственной
сфере показателями эффективности
являются обычно выручка или прибыль,
что приводит к задачам максимизации.
Именно (1.1) представляет собой формулировку
задачи максимизации целевой функции.
Решением задачи линейного программирования являются оптимальные значения управляемых переменных, которые обеспечивают максимум или минимум целевой функции.
____________________Вопрос 38____________________
Способы перехода от одной формы задачи лп к другой
Существует несколько форм записи задач линейного программирования. Рассмотрим их.
1. Общая форма записи задачи линейного программирования: необходимо найти экстремальное значение целевой функции
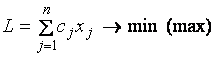 (4.1)
(4.1)
при ограничениях

на некоторые неизвестные могут быть наложены условия неотрицательности:
![]()
Здесь (и везде
далее)
![]() заданные числа
заданные числа
![]()
2. Каноническая форма записи задачи линейного программирования: необходимо найти экстремальное значение целевой функции (4.1) при ограничениях
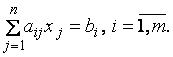
На все неизвестные наложены условия неотрицательности:
![]() (4.2)
(4.2)
3. Симметричная форма записи задачи линейного программирования. Здесь принято выделять две стандартные задачи − задачу максимизации и задачу минимизации.
3.1. Стандартная задача максимизации: необходимо найти максимальное значение целевой функции (4.1) при ограничениях
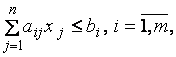
и условиях неотрицательности (4.2).
3.2. Стандартная задача минимизации: необходимо найти минимальное значение целевой функции (4.1) при ограничениях

и условиях неотрицательности (4.2).
____________________Вопрос 39____________________
