- •Расчетные задания на тестирование
- •Метод перебора.
- •Метод перебора.
- •1. Математическая постановка задачи оптимизации.
- •2. Понятие о численных методах оптимизации. Методы поиска нулевого, первого и второго порядков. Пассивные и активные (последовательные) методы поиска.
- •3. Конечно шаговые и бесконечно шаговые методы поиска. Сходимость методов. Условия останова методов поиска.
- •4. Теорема существования решения оптимизационной задачи.
- •7. Необходимые условия экстремума первого порядка (гладкие функции многих переменных).
- •9.Пассивные методы поиска экстремума.
- •10.Метод перебора.
- •11. Алгоритм оптимального пассивного поиска.
- •12.Теорема об оптимальности пассивного поиска.
- •14. Метод поразрядного поиска.
- •15. Метод дихотомий
- •16. Метод деления отрезка пополам
- •17. Метод золотого сечения
- •20. Метод средней точки
- •26 Метод симплекса.
- •27 Метод циклического покоординатного спуска.
- •29 Градиентные методы
- •30 Градиентный метод с постоянным шагом.
- •31 Градиентный метод с дроблением шага.
- •Метод наискорейшего спуска
- •Методы покоординатного спуска
- •Метод покоординатного спуска с постоянным шагом
- •Метод покоординатного спуска с дроблением шага
- •Метод Гаусса-Зейделя
- •Постановка задач линейного программирования
- •Способы перехода от одной формы задачи лп к другой
- •Базисное решение задачи лп Симплексный метод решения задач линейного программирования
- •Графический метод решения задачи лп
- •Симплекс-метод решения задачи лп
- •Метод искусственных переменных
16. Метод деления отрезка пополам
последовательный метод;
Суть метода деления отрезка пополам состоит в разбиении отрезка [a, b] (при условии f(a)f(b) < 0) на два отрезка, определении знака функции f(x) через производную в середине отрезка (a + b)/2 и выборе отрезка, на котором функция непрерывна, меняет знак и содержит решение;
Далее применяем алгоритм решения.
Краткое описание алгоритма:
Входные данные: f(x), a, b, ε.
x = (a + b)/2
Если f(a)·f(x) < 0, то b = x, иначе если f(x)·f(b) < 0, то a = x.
Если |b - a| > 2ε, то идти к 1.
x = (a + b)/2.
Выходные данные: x.
Значение x является решением с заданной точностью ε нелинейного уравнения вида f(x) = 0.
Если f(x) = 0, то x — точное решение.
!!! Дополнить рисунком (пометка самому себе)
17. Метод золотого сечения
это численный метод нахождения решения x (с заданной точностью ε), минимизирующего функцию f(x) на отрезке.
Суть метода золотого сечения состоит в разбиении отрезка [a,b] на три отрезка в пропорции золотого сечения, определении минимального значения функции f(x)из значений на границах этих отрезков и выборе нового отрезка, на котором функция содержит минимизирующее решение.
Деление отрезка продолжается до достижения необходимой точности решения ε.
Сначала находим отрезок [a,b] такой, что функция f(x) непрерывна и вогнута на отрезке, то есть f"(x)>0.
Далее применяем алгоритм.
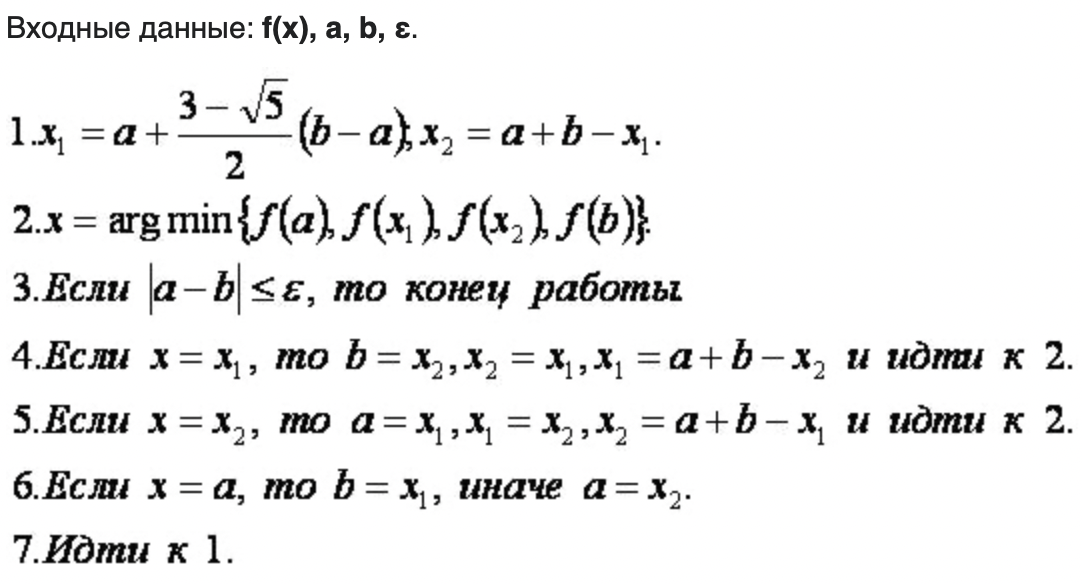
Выходные данные: x.
Значение x является минимизирующим решением для функции f(x) с заданной точностью ε.
Заметим, что для нахождения решения x, максимизирующего выпуклую функцию f(x) на отрезке, алгоритм решения модифицируется в части строки 2, она меняется на строку вида:
![]()

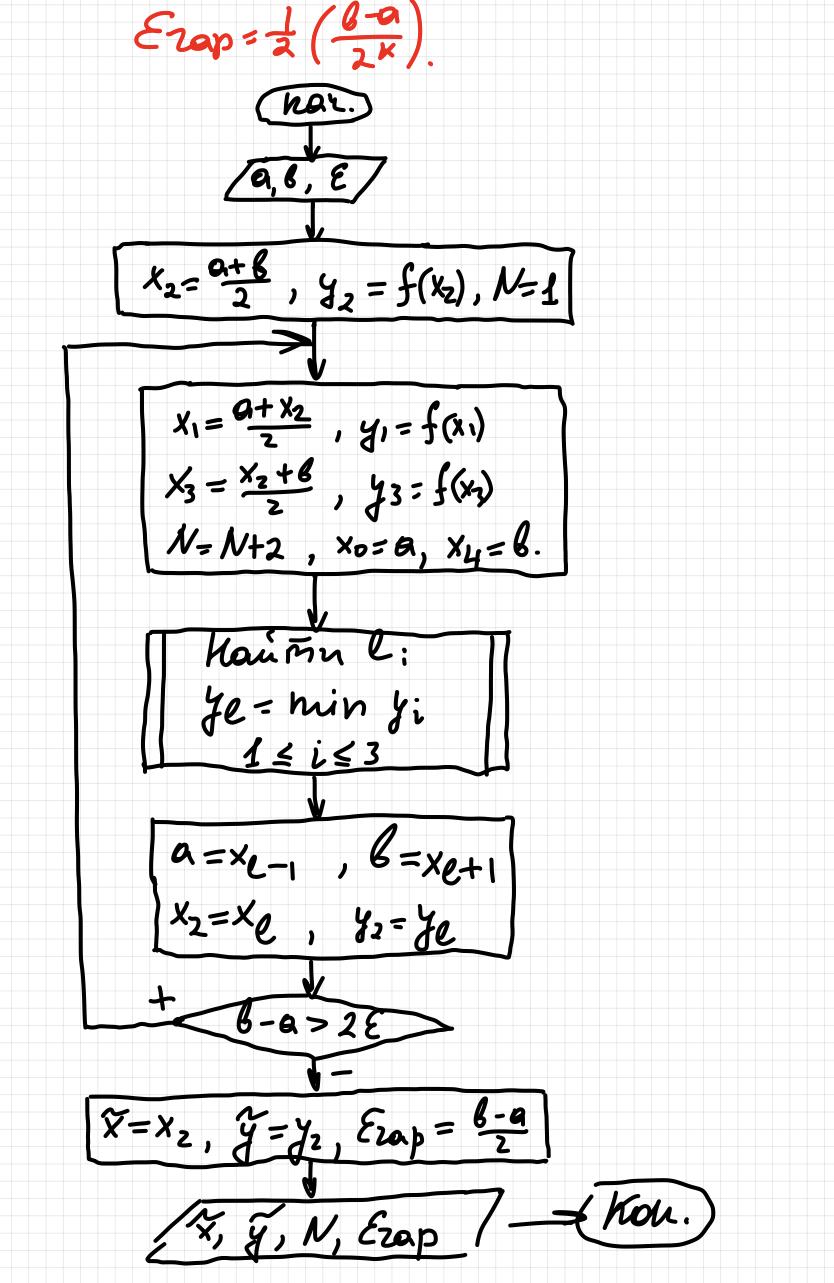
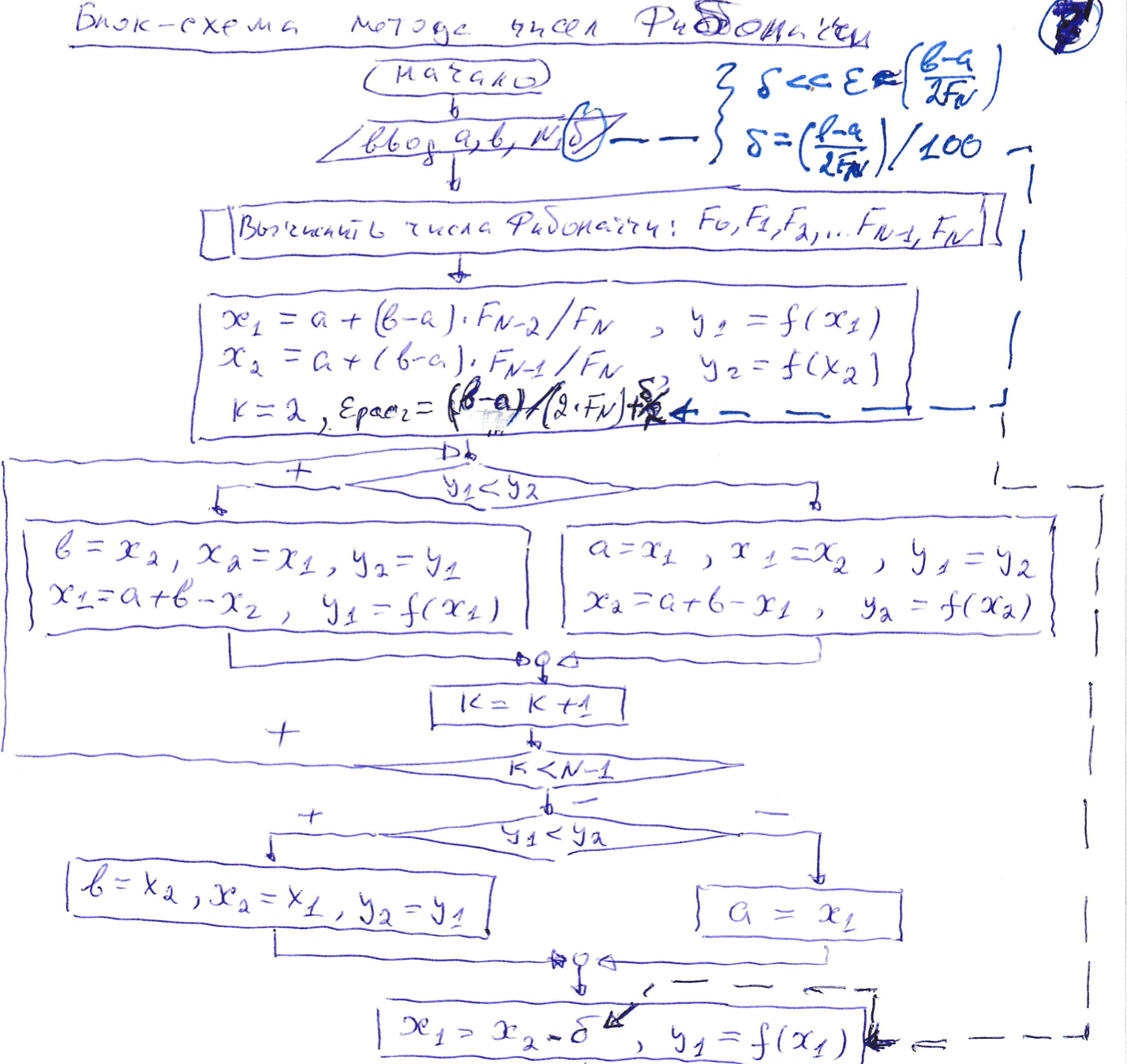
18. Метод чисел Фибоначчи
лучший метод среди методов дихотомии, деления отрезка пополам, поразрядного поиска.
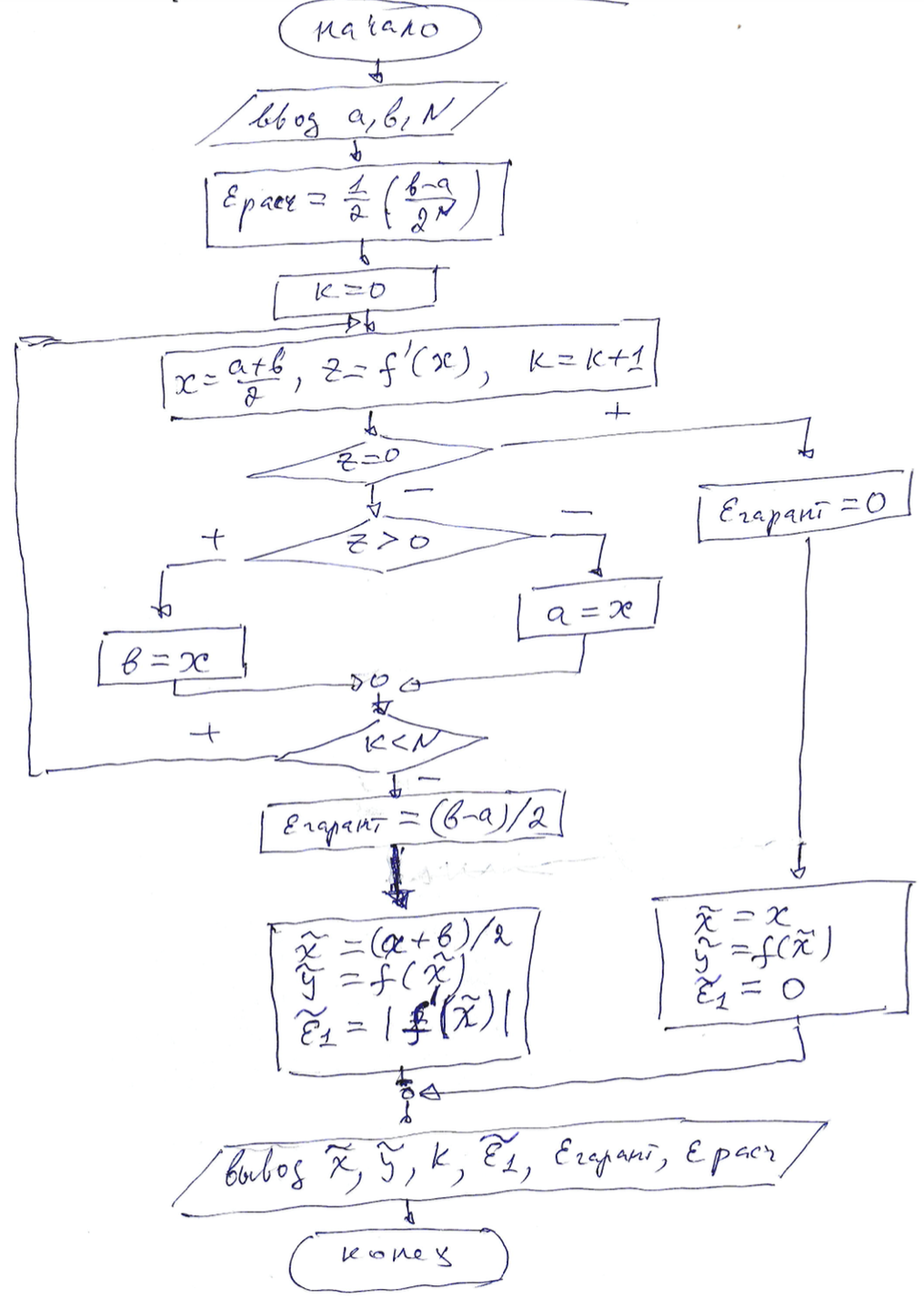
19. Метод касательных

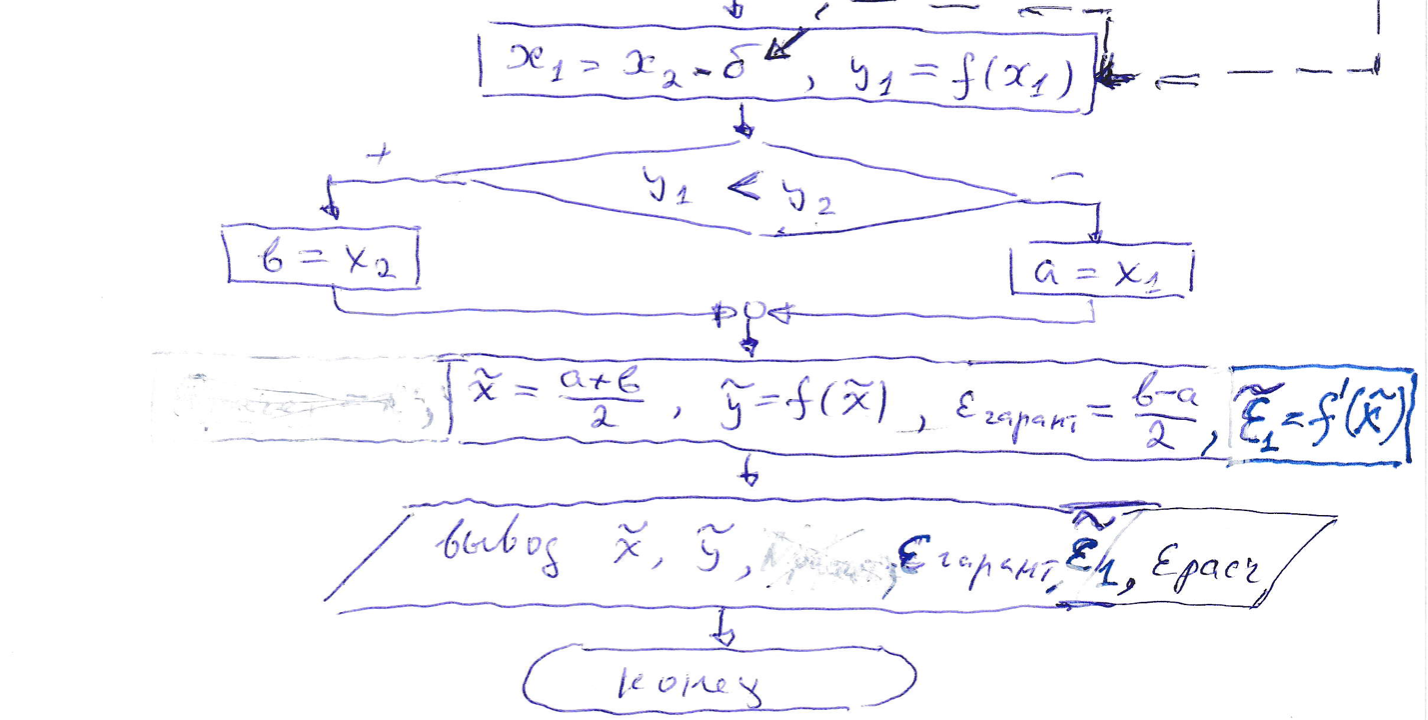
20. Метод средней точки
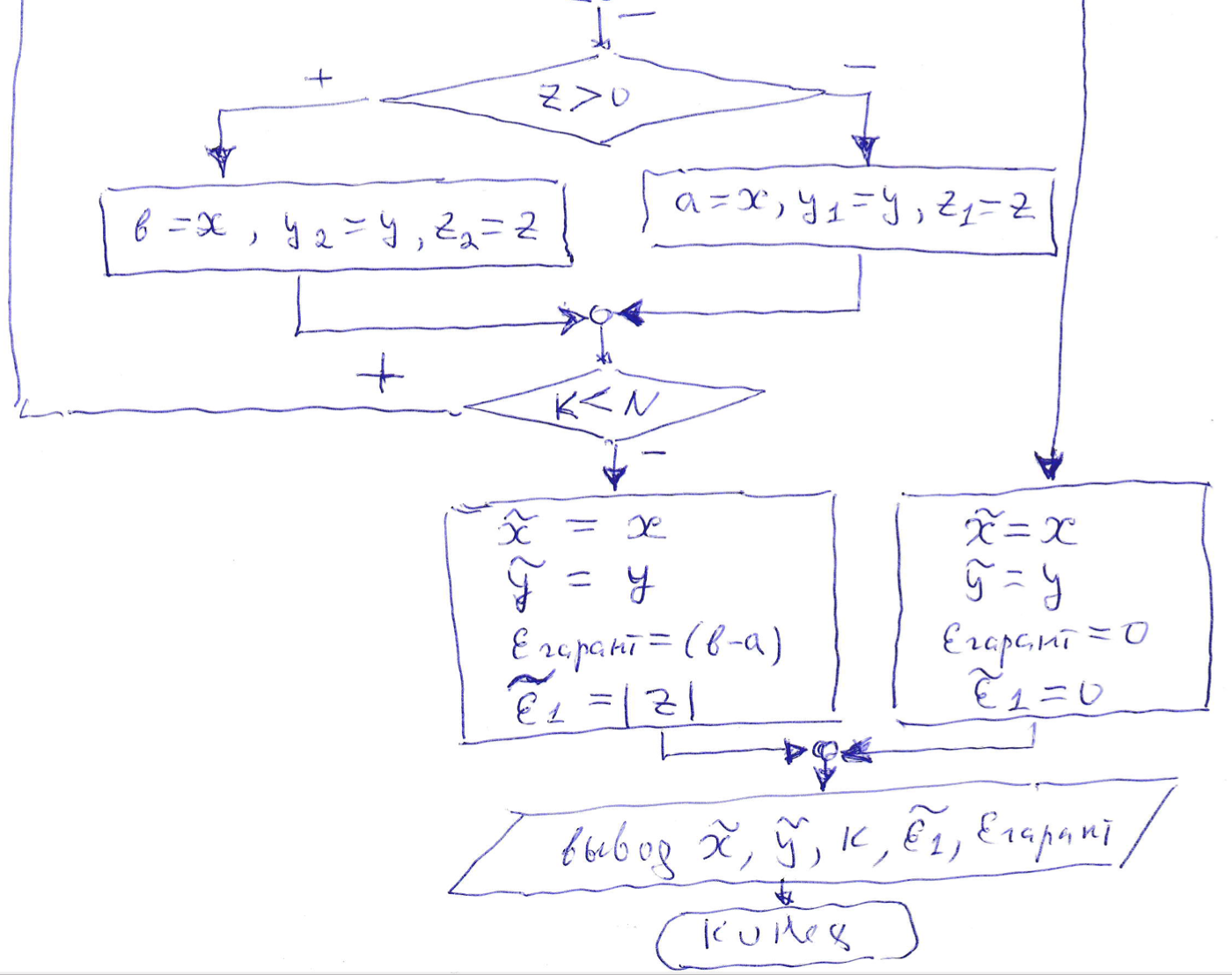
21. Метод хорд
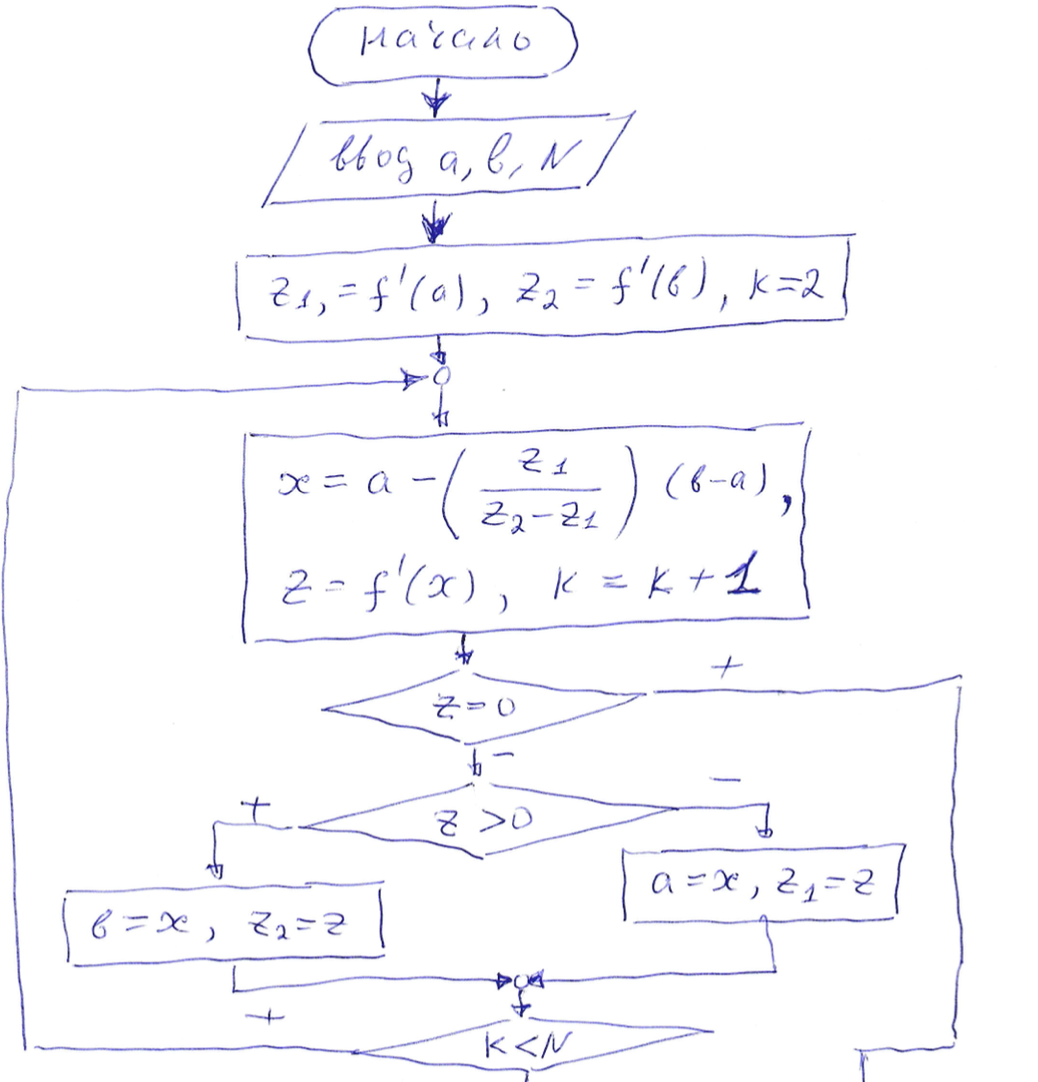

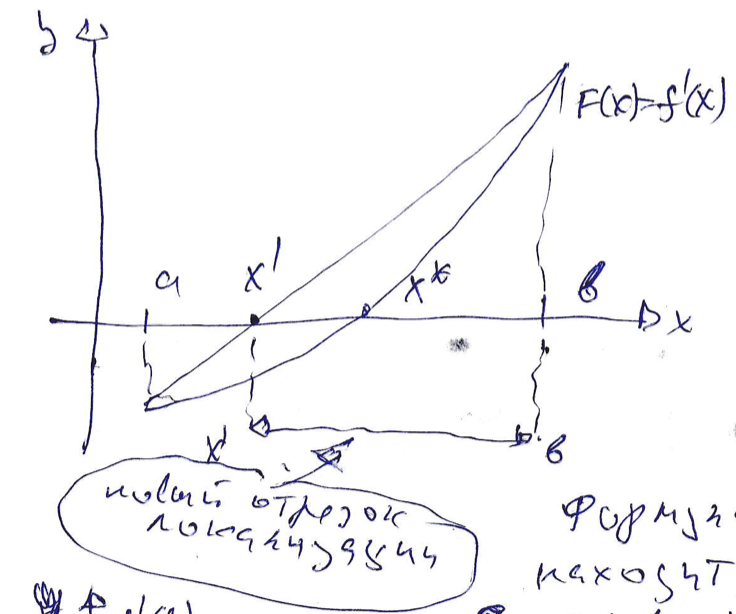
22. Метод Ньютона
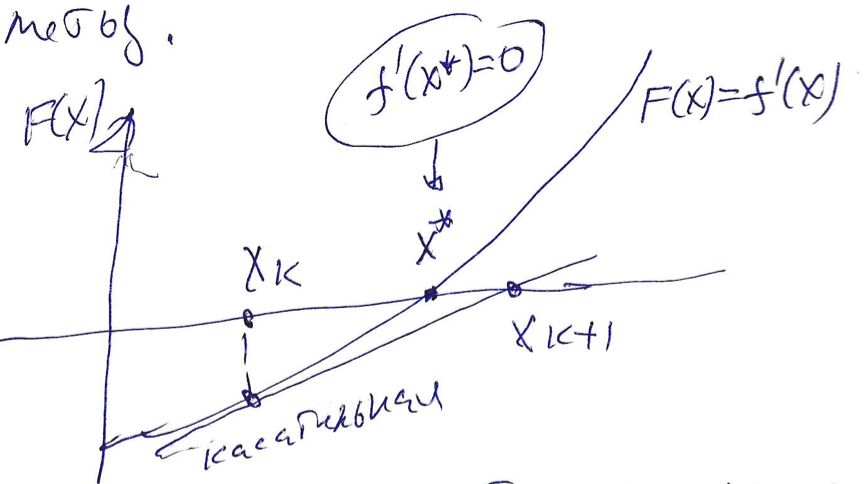
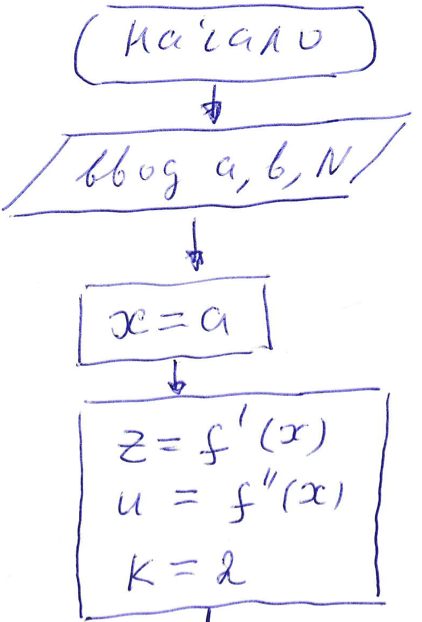
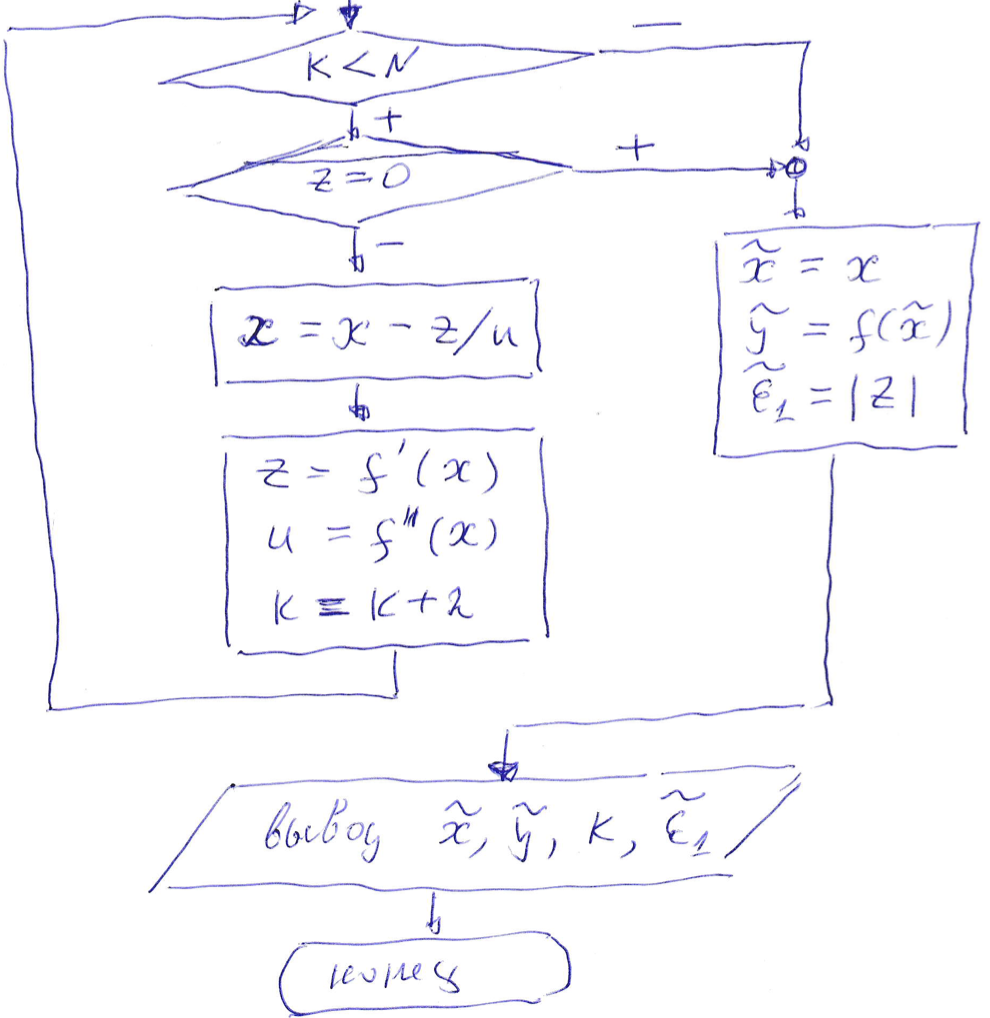
.
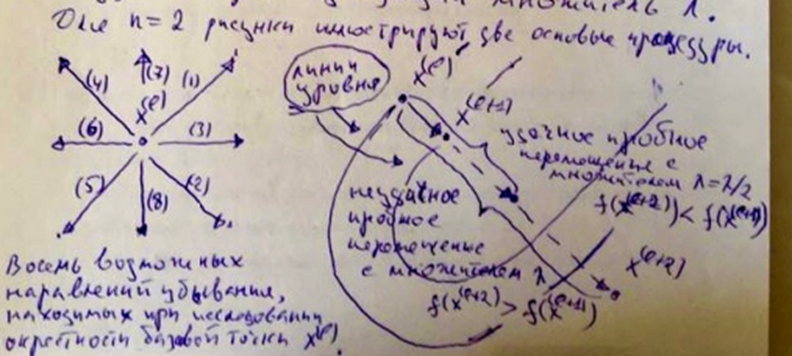
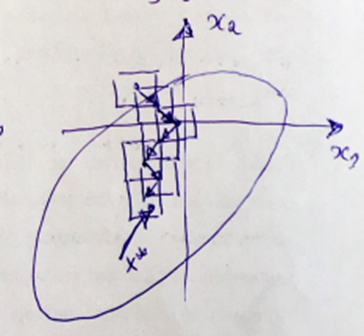
24 Поиск по образцу.
Берем базовую точку x0( нач. приближение). Вычислим в ней значение f(x0), а затем построим n-мерный куб с центром в этой точке и ребрами длиной 2h. Вычислить значения функции в вершинах куба, берем в качестве новой базовой точки ту из вершин, в которой значение ф-и меньше f(x0) и повторим процедуру для выбора следующей базовой точки и построения образца .Если такой вершины не оказалось, то оставим прежнюю базовую точку x0 и построим куб с уменьшенной длиной ребер, например h. Поиск заканчивается, когда длинна ребра станет меньше заданного числа E>0
.
25 Метод конфигурации.
Алгоритм включает в себя два основных этапа поиска.
а) В начале обследуется окрестность выбранной точки (базисной точки), в результате находится приемлемое направление спуска; Если значение ф-и в пробной точке меньше чем в исходной, шаг считается удачным. В противном случае возвращаемся назад и делаем шаг в противоположном направлении. После перебора всех координатных исследования окрестности базовой точки – конец. В результате поиска получена точка x(l+1), если исследование оказалось неудачным x(l+1)=x(l), уменьшаем шаг в 2 раза и продолжаем процедуру.
б) Затем в этом направлении находится точка с наименьшим значением целевой функции. Таким образом находится новая базисная точка. Если же пробное перемещение оказалось неудачным, то уменьшаем ускоряющий множитель, то уменьшаем ускоряющий коэффициент в 2 раза и осуществляем пробное перемещение в точку x(l+2) с этим множителем. Процесс продолжается пока не найдется подходящий множитель.