
- •Расчетные задания на тестирование
- •Метод перебора.
- •Метод перебора.
- •1. Математическая постановка задачи оптимизации.
- •2. Понятие о численных методах оптимизации. Методы поиска нулевого, первого и второго порядков. Пассивные и активные (последовательные) методы поиска.
- •3. Конечно шаговые и бесконечно шаговые методы поиска. Сходимость методов. Условия останова методов поиска.
- •4. Теорема существования решения оптимизационной задачи.
- •7. Необходимые условия экстремума первого порядка (гладкие функции многих переменных).
- •9.Пассивные методы поиска экстремума.
- •10.Метод перебора.
- •11. Алгоритм оптимального пассивного поиска.
- •12.Теорема об оптимальности пассивного поиска.
- •14. Метод поразрядного поиска.
- •15. Метод дихотомий
- •16. Метод деления отрезка пополам
- •17. Метод золотого сечения
- •20. Метод средней точки
- •26 Метод симплекса.
- •27 Метод циклического покоординатного спуска.
- •29 Градиентные методы
- •30 Градиентный метод с постоянным шагом.
- •31 Градиентный метод с дроблением шага.
- •Метод наискорейшего спуска
- •Методы покоординатного спуска
- •Метод покоординатного спуска с постоянным шагом
- •Метод покоординатного спуска с дроблением шага
- •Метод Гаусса-Зейделя
- •Постановка задач линейного программирования
- •Способы перехода от одной формы задачи лп к другой
- •Базисное решение задачи лп Симплексный метод решения задач линейного программирования
- •Графический метод решения задачи лп
- •Симплекс-метод решения задачи лп
- •Метод искусственных переменных
4. Теорема существования решения оптимизационной задачи.

7. Необходимые условия экстремума первого порядка (гладкие функции многих переменных).
9.Пассивные методы поиска экстремума.
10.Метод перебора.
Метод перебора или равномерного поиска является простейшим методом минимизации и заключается в следующем. Разобьем отрезок [a, b] на N+1 равных частей точками деления xi = a + i*((b-a)/(N+1)), где i=1,2,3..N. Вычислим значения f(x) в точках 𝑥𝑖 . Найдем точку xl , для которой значение целевой функции минимально
![]() Точность
найденного решения 𝑥̃определяется по
формуле:
Точность
найденного решения 𝑥̃определяется по
формуле:
 ,
где
,
где
Если
необходимо найти приближенное решение
с заданной точностью ε, то минимальное
число экспериментов N для достижения
этой точности определяется из условия
N
= Nрасч =
 {N:N
{N:N }
}
11. Алгоритм оптимального пассивного поиска.
Минимаксный метод поиска, в котором информация о значениях функции, вычисленных в предшествующих точках, не может быть использована, называют оптимальным пассивным поиском.
Алгоритм:
Отрезок [a,b] исходный отрезок неопределенности. Пусть N - число точек, в которых необходимо провести вычисления целевой функции f(x), т.е. N экспериментов. Точки, в которых необходимо провести эксперименты, определяются следующим образом:
Если N = 2k-1 - нечетное, то xi = a + i*((b-a)/(N+1)), где i=1,2,3..N
Если
N = 2k - четное,
то
x2i = a + i*((b-a)/(k+1)), x2i-1 =x2i -
 где
i=1,2,3..k
где
i=1,2,3..k
Среди вычисленных значений {f(xi)} (i=1,N), ищется точка xj, в которой достигается минимум: f(xj)= min f(xi) (min от 1 до N)
Найденная
точка принимается за приближенное
решение задачи
 = xj. Исходный отрезок неопределенности
[a,b] после экспериментов в N точках
сужается до [xj-1,xj+1], длина которого равна:
= xj. Исходный отрезок неопределенности
[a,b] после экспериментов в N точках
сужается до [xj-1,xj+1], длина которого равна:

Точность
найденного решения
равна половине отрезка неопределенности,
т.е.
 ,
где
,
где
 и
x* - точное решение.
и
x* - точное решение.
12.Теорема об оптимальности пассивного поиска.
Т. 1)Если N=2k-1, то предлагаемый алгоритм является оптимальным.
2)Если N=2k то оптимального алгоритма не существует.
14. Метод поразрядного поиска.
представляет собой усовершенствованный метод перебора;
поиск точки минимума осуществляется с переменным шагом.
Краткое описание алгоритма:
Вводится начало и конец отрезка a, b и точность E.
Выбор
начального
шага h =
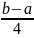 ;
;
Задаем
 =
a. Вычисляем F(
),
N=1;
=
a. Вычисляем F(
),
N=1;Предположим, что мы идем вправо +h.
 .
Вычисляем значение F(
.
Вычисляем значение F( ),
N=N+1;
),
N=N+1;Сравнить F( ) и F( ). Если F( ) >F( ), переходим к шагу 5, иначе к шагу 6;
= , F( )=F( ). Проверка на то, не вышли ли мы на границу a< <b?
Если да: идем на шаг 3;
Если нет: идем на шаг 7.
Функция начала расти, переходим шаг 7.
|h|<=E?
Если да: “точность достигнута” x~ = , y~= F( ), Eгар = h. И выводим рез-ты;
Если нет: “точность не достигнута - меняем направление”
= F(
)=F(
),
h = -h/4 и идем на шаг 3.
F(
)=F(
),
h = -h/4 и идем на шаг 3.
15. Метод дихотомий
Этот метод является методом прямого поиска;
В нем при поиске экстремума целевой функции используются только вычисленные значения целевой функции.
Краткое описание алгоритма:
Вводится a, b, E, sigma. Причем sigma << E. N= 0;
x = (a+b)/2;
 ;
;
 ;
N=N+2;
;
N=N+2; <
<
Если да: b = x+sigma;
Нет: a = x - sigma;
Проверка условия достижения заданной точности: b-a > 2E?
Если да: возвращаемся к шагу 2;
Нет: x~ = (a+b)/2; y~ = f(x~0); Eгар = (b-a)/2. Вывод x~, y~, Eгар, N.

