1 семестр ИКТ / лаба №3

Отчет по лабораторной работе №3

Упражнение 3.1: Дан параллелограмм ABCD, известны координаты трех его точек A(-2 0), B(1 2), C(1 -1). Найти координаты четвертой вершины D параллелограмма. Изобразить разными цветами векторы, используемые в решении задачи.

>> OA=[-2 0]

OA = -2 0

>> OB=[1 2]

OB =1 2

>> OC=[1 -1]

OC = 1 -1

>> AB=OB-OA

AB = 3 2

>> BC=OC-OB

BC = 0 -3

>> AC=OC-OA

AC = 3 -1

>> hold on,grid on

>> quiver(-2,0,AB(1),AB(2),0)

>> quiver(1,2,BC(1),BC(2),0)

>> quiver(-2,0,BC(1),BC(2),0)

>> quiver(-2,-3,AB(1),AB(2),0)

>> OD = BC+OA

OD = -2 -3

Упражнение 3.2

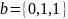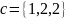Доказать, что векторы , и образуют базис. Изобразить эти векторы и координатные оси.

>> a =[1 -2 0]

>> b =[ 0 1 1]

>> c =[1 2 2]

>> A =[a; b;c]

A =

1 -2 0

0 1 1

1 2 2

>> det(A)

ans = -2

Определитель не равен нулю, значит вектора образуют базис. Доказано

>> hold on

>> grid on

>> axis square

>> xlabel('X'),ylabel('Y'),zlabel('Z')

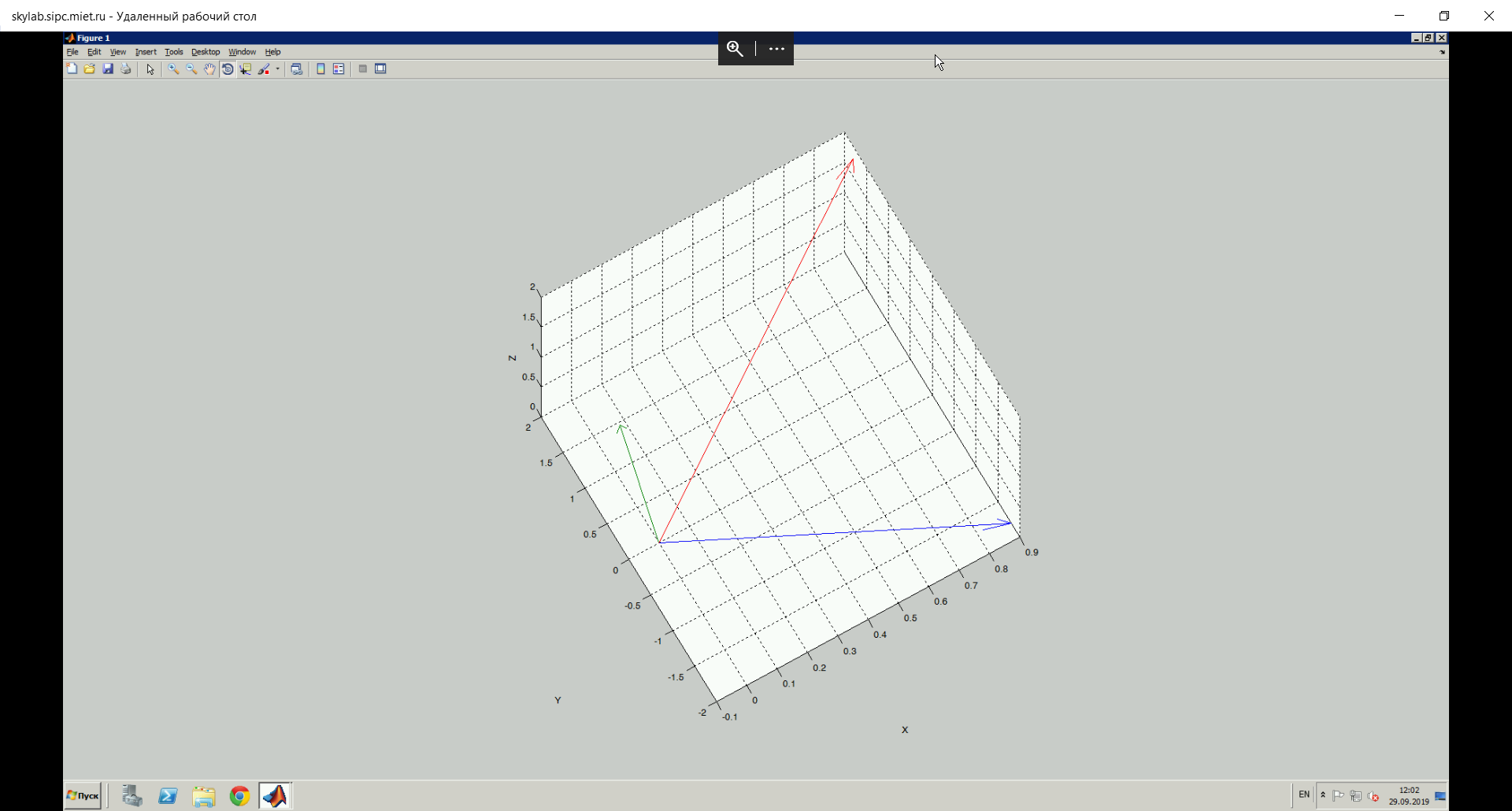
>> quiver3(0,0,0,a(1),a(2),a(3))

>> quiver3(0,0,0,b(1),b(2),b(3))

>> quiver3(0,0,0,c(1),c(2),c(3))

Упражнение 3.3

Проверить являются ли векторы линейно зависимыми и, если возможно, разложить вектор по этим векторам (при решении системы использовать формулы Крамера или обратную матрицу). Векторы задать в символьном виде.

1. 

2. 

1.

>> syms a b c

>> p = a – b + c

>> q =b – a - c

>> r =b - c

>> s = a + b + c

>> a =[1 -2 0]

>> b =[ 0 1 1]

>> c =[1 2 2]

>> p = a - b + c

>> q =b - a - c

>> r = b - c

>> A = [p;q;r]

A =

2 -1 1

-2 1 -1

-1 -1 -1

>> det(A)

ans = 0

Вектора образуют базис(определитель равен нулю), значит, они не зависимы линейно и, следовательно, вектор s нельзя разложить по этим векторам.

2.

>> a =[1 -2 0]

>> b =[ 0 1 1]

>> c =[1 2 2]

>> p = a - b + c

>> q = b+a

>> r = b-c

>> A = [p;q;r]

A =

2 -1 1

1 -1 1

-1 -1 -1

>> det(A)

ans = 2

>> s = a+b+c

>> s1 = [2;1;3]

s1 =

2

1

3

>> x = inv(A)*s1

x =

-1

2

-2

Упражнение 3.4

Даны три точки A(-2, 0), B(3, 4), C(4, -1). Найти величины углов треугольника АВС. Проверить свойство суммы углов треугольника. Сделать рисунок.

a=[-2 0]

b=[3 4]

c=[4 -1]

ab=[b-a]

ac=[c-a]

bc=[c-b]

A=ab*ac'

A=A/(norm(ab)*norm(ac))

A=acosd(A)

A = 48.1221

C =ac*bc'

C=C/(norm(ac)*norm(bc))

C=acosd(C)

C = 69.2277

B=(-ab)*(bc)'

B=B/(norm(ab)*norm(bc))

B=acosd(B)

B =62.6501

A+B+C

>> hold on,grid on,axis square

>> xlabel('X'),ylabel('Y'),zlabel('Z')

>> quiver(-2,0,5,4,0)

>> quiver(3,4,1,-5,0)

>> quiver(4,-1,-6,1,0)

Упражнение 3.5

Найти векторное произведение векторов и с помощью определителя третьего порядка и проверить решение стандартной функцией cross(a,b)

>> a=[1 2 0]

>> b=[2 1 0]

>> syms i j k

>> A=[i j k;a;b]

A =

[ i, j, k]

[ 1, 2, 0]

[ 2, 1, 0]

>> det(A)

ans = (-3)*k

>> ab=cross(a,b)

ab = 0 0 -3

Упражнение 3.6

Вычислить площадь треугольника с вершинами и Изобразить плоскость треугольника.

>> a =[1 3 -1]

>> b=[2 -1 4]

>> c=[5 0 3]

>> ab = b-a

ab = 1 -4 5

>> ac = c-a

ac = 4 -3 4

>> bc = b-c

bc = -3 -1 1

>> A = [a;b;c]

A =

1 3 -1

2 -1 4

5 0 3

>> S = 1/2*det(A)

S = 17

fill3(a,b,c,'m')

Упражнение 3.7

С помощью смешанного произведения определить значение λ, при котором векторы , , 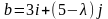будут компланарны. Определить ориентацию тройки abc. При решении уравнения используйте функцию solve

>> syms x

>> A =[-1 2 4;3 (5-x) 0; 2 4 -5]

A =

[ -1, 2, 4]

[ 3, 5 - x, 0]

[ 2, 4, -5]

>> det(A)

ans =3*x + 63

Векторы будут компланарны,если определитель будет равен 0. Решим уравнение:

>> solve('3*x + 63=0')

ans =-21

Векторы образуют правую/левую тройку тогда и только тогда, когда их смешанное произведение больше/меньше нуля. Значит, вектора a b c образуют левую тройку.

Упражнение С1:

Вычислить объем пирамиды ABCD, если известно, что

>> a = [3 4 0]

>> b =[-3 0 1]

>> c =[0 2 5]

>> A =[a;b;c]

A =

3 4 0

-3 0 1

0 2 5

Найдем объем пирамиды, воспользовавшись свойствами:

>> V = 1/6*det(A)

V =9

Упражнение С2:

Ознакомьтесь самостоятельно со встроенной функцией norm. Для трех произвольных векторов различной размерности найдите их длины:

1)

>> a =[2 7 10]

>> norm(a)

ans = 12.3693

>> sqrt(a(1)^2+a(2)^2+a(3)^2)

ans =12.3693

2)

>> b = [1 12 6]

>> sqrt(b(1)^2+b(2)^2+b(3)^2)

ans =13.4536

>> norm(b)

ans = 13.4536

3)

>> c =[7 16 2]

>> sqrt(c(1)^2+c(2)^2+c(3)^2)

ans =17.5784

>> norm(c)

ans = 17.5784