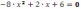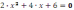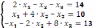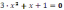Лабораторная работа №4 решение квадратных уравнений систем линейных алгебраических уравнений(слау) средствами ms excel
Цели: Научиться использовать функциюЕСЛИ, для решения квадратного уравнения, овладеть технологией решения систем линейных алгебраических уравнений средствами MS Excel. Научиться приемам работы с матрицами.
Вопросы, изучаемые в работе
Решение квадратных уравнений.
Приемы работы с матрицами.
Решение систем линейных алгебраических уравнений.
Проверка решения.
Общие пояснения
Табличные формулы или формулы массива – очень мощное вычислительное средство Excel, позволяющее работать с блоками рабочего листа как с отдельными ячейками. Табличные формулы в качестве результата возвращают массив значений. Поэтому перед вводом такой формулы необходимо выделить диапазон ячеек, куда будут помещены результаты. Потом набирается сама формула. Ввод ее в выделенный диапазон ячеек осуществляется нажатием комбинации клавиш [Ctrl+Shift+Enter]. Формула вводится во все ячейки выделенного интервала. При активизации любой ячейки из интервала, содержащего формулу массива, в строке формул отображается введенная формула, заключенная в фигурные скобки. Именно фигурные скобки являются признаком табличной формулы. Для выделения всего блока, содержащего табличную формулу, необходимо выделить одну из его ячеек, после чего нажать комбинацию клавиш [Ctrl+/].Невозможно редактировать содержимое только одной ячейки из интервала с табличной формулой. Изменить можно только весь блок целиком, для чего он и должен быть предварительно выделен.
Общие рекомендации по подготовке и обработке данных в электронных таблицах MicrosoftExcel
К простейшим операциям с матрицами принято относить следующие: сложение и вычитание матриц, умножение и деление матрицы на число, перемножение матриц, транспонирование, вычисление обратной матрицы. Умножение (деление) матрицы на число, сложение (вычитание) матриц в Excel реализуются достаточно просто-с помощью обычных формул (поэлементное сложение или вычитание, умножение или деление на число), либо с использованием табличных формул, как это было описано выше. Для остальных матричных операций в Excel предусмотрены функции рабочего листа из категории «Арифметические и тригонометрические функции»:
МОПРЕД(матрица) – вычисление определителя матрицы,
МОБР(матрица) – вычисление обратной матрицы,
МУМНОЖ(матрица1;матрица2) – произведение матриц,
ТРАНСП(матрица) – транспонирование матрицы.
Первая из этих функций в качестве результата возвращает число (определитель матрицы), поэтому вводится как обычная формула [Enter]. Последние три возвращают блок ячеек, поэтому должны вводиться как табличные формулы [Ctrl+Shift+Enter].
Функция ЕСЛИ часто используется вExcel для решения многих задач. Часто используется при решении уравнений и их систем.
Функция ЕСЛИпроверяет, выполняетсяли условие, и возвращает одно значение, если оно выполняется, и другое значение, еслинет.
Синтаксис функции ЕСЛИ:
ЕСЛИ(лог_выражение; [значение_если_истина]; [значение_если_ложь]).
лог_выражение –это значение или выражение, которое при вычислении дает значение ИСТИНА или ЛОЖЬ.
Порядок создания документа
Запустите программу MSExcel.
В программе Excel создайте новую книгу.
Сохраните созданную книгу (созданные документы размещать ТОЛЬКО в папках своей группы).
Задание 1
Подготовить электронную таблицукорней квадратного уравнения
Вычислить дискриминант и корни уравнения
Переименовать рабочий лист в решение квадратного уравнения
Порядок выполнения работы
Открыть (создать) новый рабочий лист
На рабочем листе создать таблицу, согласно макету, представленному на рисунке 4.1:
Рисунок 4.1. Макет таблицы к лабораторной работе №4
В ячейкиА3, B3,C3 ввести значения согласно варианту.
В ячейку D3 ввести формулу вычисления дискриминанта.
В ячейки Е3, F3ввести формулы вычисления корней с помощью функции ЕСЛИ
Задание 2
Подготовить электронную таблицу, на отдельном листе, в которойбудет производиться матричный способ решения СЛАУ.
Записать формулы решения уравнений.
Переименовать рабочий лист в матричный способ решения СЛАУ.
Порядок выполнения работы
Открыть(создать) новый рабочий лист.
На рабочем листе создайте таблицу, согласно макету, представленному на рисунке. 4.2:
Рисунок 4.2. Макет таблицы к лабораторной работе №4
Ввести в таблицу значения матрицы коэффициентов А3,3, согласно вашему варианту.
Ввести в таблицу значения вектора В3,1, согласно вашему варианту.
Выделить ячейки, в которые будут записываться значения обратной матрицы.
Вызвать мастер функций, выбрать функцию МОБР для вычисления обратной матрицы.
Ввести в диалоговое окноадрес исходной матрицы коэффициентов.Нажать клавиши [Ctrl+Shift+Enter]. В выделенных ячейках появятся значения обратной матрицы.
Выделить место для результата (вектор неизвестных) Х3,1.
Вызвать мастера функций и найти функцию МУМНОЖ.
Ввести в диалоговое окно два адреса:
– адрес обратной матрицы (массив1);
– адрес вектора правых частей (массив2).
Нажатьклавиши [Ctrl+Shift+Enter]
Задание 3
Подготовить электронную таблицу, на отдельном листе, в которойбудет производиться решение СЛАУ методом Крамера.
Записать формулы решения уравнений.
Переименовать рабочий лист в Метод Крамера.
Порядок выполнения работы
Открыть(создать) новый рабочий лист.
На рабочем листе создать таблицу, согласно макету, представленному на рисунке 4.3
Рисунок 4.3. Макет таблицы к лабораторной работе №4
Ввести в таблицу значения матрицы коэффициентов А3,3, с использованием абсолютных ссылок со 2 листа.
В ячейки B6:D8 записать матрицу с заменой 1-го столбца на столбец свободных членов B.
Аналогично произвести с B9:D11, заменив 2 столбец, и с B12:D14, заменив 3 столбец.
Далее, воспользовавшись функцией МОПРЕД(матрица), вычислить определитель матрицы (главный определитель) и записать ее в Н10.
В ячейках Н12-Н14 вычислить определители матриц Аi(вспомогательные определители) с помощью функцией МОПРЕД(матрица).
С помощью функции ЕСЛИ вычислить корни уравнений, если «главный определитель»=0 то решений нет, иначе «вспомогательный определитель»/ «главный определитель».
Задание 4
Подготовить электронную таблицу, на отдельном листе, в которой будет производиться решение СЛАУ с помощью поиска решений.
Записать формулы решения уравнений.
Переименовать рабочий лист в поиск решений.
Порядок выполнения работы
Открыть(создать) новый рабочий лист.
Ввести в таблицу значения матрицы коэффициентов А3,3, с использованием абсолютных ссылок со 2 листа, согласно макету на рисунке 4.4.
Ввести в таблицу значения вектора В3,1, с использованием абсолютных ссылок со 2 листа.
Рисунок 4.4.Макет таблицы к лабораторной работе №4
Далее, формулой
,
вычислить целевую функцию решения
уравнений и записать в ячейку С6, С7,
С8.Вызвать «поиск решений» из вкладки Данные, и заполнить поля в соответствии с рисунком 4.3
Рисунок 4.3. Диалоговое окно поиска решений
Варианты заданий
Таблица 4.1. Индивидуальные задания к лабораторной работе №4
№ вар |
Квадратное уравнение |
Система линейных уравнений |
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
|
9 |
|
|
10 |
|
|
11 |
|
|
12 |
|
|
13 |
|
|
14 |
|
|
15 |
|
|
16 |
|
|
