Добавил:

NastiaSokolova97 nastia.sokolowa2017@yandex.ru Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Российский государственный гидрометеорологический университет

Предмет:

Высшая математика

Файл:

ДифУр-яЧ1-2.pdf

Скачиваний:

Добавлен:

19.02.2024

Размер:

449.07 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 63 4 5 6 > Следующая >>>

Общее решение однородного уравнения таково: yо = C1ex +C2e−x , а общее решение уравнения y = yн + yо = e2x (0.3cos x +0.6sin x) +C1ex +C2e−x . ▼

7. Уравнение колебаний

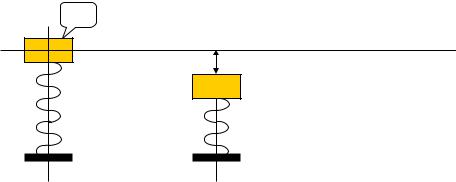
Рассмотрим задачу о механических колебаниях. Пусть груз массы m покоится на упругой рессоре, закрепленной в некоторой точке A (рис. 8.1).

Положение равновесия

A A

Рис. 8.1

Отклонение груза от положения равновесия обозначим переменной y. Будем считать положительным отклонение вниз и отрицательным – отклонение вверх. В положении равновесия сила веса уравновешивается

упругостью рессоры. Предположим, что сила F1 , стремящаяся вернуть груз в положение равновесия (так называемая восстанавливающая сила), пропорциональна отклонению, т. е.

F1 = −ky (k = const, k > 0)

(1)

(k – положительная постоянная для данной рессоры, так называемая жесткость рессоры). Предположим еще, что движению груза препятствует сила сопротивления F2 , направленная в сторону, противоположную направ-

лению движения и пропорциональная скорости v движения груза, т.е.

= −λv = −λ

d y

(λ = const, λ > 0) .

(2)

Составим дифференциальное уравнение движения груза на рессоре. В соответствии со вторым законом

Ньютона получаем mw = F

+ F

, где

w =

d 2 y

, или

dt2

d 2 y

= −k y −λ

d y

(k > 0, λ

> 0) .

(3)

dt2

Уравнение (3) является линейным дифференциальным уравнением второго порядка с постоянными коэф-

фициентами, его можно записать в виде
	d 2 y	+ p		d y	+ q y = 0			,	(4)
	dt2			dt

где		λ				k
	p =		,	q =			.		(5)
		m
						m

Уравнение (4) называется уравнением свободных колебаний.

Рассмотрим случай, когда точка A прикрепления рессоры совершает вертикальное движение по закону z = ϕ(t) .

Это имеет место тогда, когда нижний конец рессоры прикреплен к катку, движущемуся вместе с рессорой и грузом по неровности (рис. 8.2).

При этом восстанавливающая сила F1 будет выражаться формулой F1 = −k(y +ϕ(t)), а сила сопротивления F2 – формулой F2 = −λ(y′+ϕ′(t)).

							y
							z = ϕ(t)
							t
			Рис. 2
Дифференциальное уравнение движения груза на рессоре принимает вид
m	d 2 y	= −k	(y +ϕ(t))−λ(y			′	′	(6)
m	dt2	= −k	(y +ϕ(t))−λ(y				+ϕ (t))	(6)
или
		d 2 y	+ p	d y	+ q y =	f (t) ,		(7)
		dt2	+ p	dt	+ q y =	f (t) ,		(7)
		dt2		dt
где	= λ		k ,	f (t) = − kϕ(t) + λϕ′(t) .
p	= λ	, q =	k ,	f (t) = − kϕ(t) + λϕ′(t) .				(8)
	m		m				m
Уравнение (7) является неоднородным линейным дифференциальным уравнением второго порядка с по-
стоянными коэффициентами. Это уравнение называется уравнением вынужденных колебаний.

7.1. Свободные колебания

Рассмотрим уравнение свободных колебаний, т. е. уравнение

d 2 y

+ p

d y

+ q y =

0 .

Соответствующее

характеристическое уравнение k2 + pk + q = 0 имеет корни k = −

−

−q,

= −

−q , в зависи-

мости от которых получаем общее решение уравнения свободных колебаний.

F2 = 0 ,

тогда

λ = 0 и p = 0

Рассмотрим сначала случай, когда отсутствует сила сопротивления, т.

е.

(см. (2) и (5)). Характеристическое уравнение в этом случае принимает вид k2 + q = 0 и имеет комплексные

корни k1 = − iβ,	k2 = iβ , где β =					q	, поэтому общее решение уравнения свободных колебаний	y′′+ q y = 0
определяется формулой							y = C1 cos βt +C2 sin βt .	(1.1)
							y = C1 cos βt +C2 sin βt .	(1.1)
Преобразуя правую часть этой формулы, введя новые постоянные A и ϕ0 : C1 = Asinϕ0 , C2								= Acosϕ0 ,
			= arctg	C1	.
откуда A = C2	+C2 , ϕ	0		C1
откуда A = C2	+C2 , ϕ
1	2			C2
				C2
Подставляя выражения для C1 и C2 в формулу (1.1), получаем общее решение
							y = Asin(βt +ϕ0 ) ,	(1.2)

где A и ϕ0 – произвольные постоянные величины. Колебания в данном случае называются гармоническими. Интегральными линиями являются синусоиды.

Определение 1. Периодом колебаний называется промежуток времени T, за который аргумент синуса изменится на 2π .

В рассматриваемом случае T = 2βπ .

Определение 2. Частотой колебаний называется число колебаний за время 2π .

В данном случае частота равна β .

Определение 3. Амплитуда колебаний есть величина наибольшего отклонения от положения равновесия.

Из формулы (1.2) видно, что это наибольшее отклонение равно A .

Определение 4. Начальной фазой называется величина ϕ0 .

Исследуем случай, когда F ≠ 0, т. е.

з ≠ 0 . Рассмотрим три возможности:

< q,

> q,

= q .

Если

< q , то характеристическое уравнение k2 + pk + q = 0 имеет комплексные корни

k =α +iβ, k

=α −iβ , где α = −

0, β = q −

Общее решение уравнения (4) определяется формулой

y = eαt (C

cos βt +C

sin βt)

(1.3)

или

y = Aeαt sin(βt +ϕ0 ) .

(1.4)

В качестве амплитуды здесь рассматривают величину

Aeαt

зависящую от времени. Поскольку α < 0 ,

то эта величина стремится к нулю при t → ∞, и колебания называются затухающими.

Если

> q , то характеристическое уравнение имеет вещественные отрицательные различные корни k

и k2 . Общее решение уравнения определяется формулой

y = C ek1t +C

ek2t

< 0, k

< 0) ,

(1.5)

из которой видно, что y → 0 при t → ∞ . Колебаний в данном случае не будет (сила сопротивления велика по сравнению с жесткостью рессоры).

Если

= q , то корни характеристического уравнения равны между собой

= k

= −

< 0)

, поэтому

общее решение уравнения (4) определяется формулой

y = (C

t)e−

t .

(1.6)

Здесь также y → 0 при t → ∞ , однако, y стремится медленнее, чем в предыдущем случае.

7.2. Вынужденные колебания

Обратимся к уравнению вынужденных колебаний, т. е. к уравнению (7). Рассмотрим практически важный случай, когда возмущающая внешняя сила является периодической и изменяется по закону f (t) = asinωt .

В этом случае уравнение (7) запишется так:

	d 2 y	+ p	d y	+ q y = asinωt .		(2.1)
	dt2	+ p	dt	+ q y = asinωt .		(2.1)
	dt2		dt
Исследуем уравнение (2.1) при p = 0 (сила сопротивления отсутствует) и p ≠ 0,					p2	< q .
					4	< q .
					4

Если сила сопротивления отсутствует, т. е. p = 0 , то уравнение вынужденных колебаний принимает вид

d 2t + q y = asinωt . dt2

Соответствующее однородное уравнение имеет общее решение

yн =C1 cos βt +C2 sin βt (β2 = q)

или

yн = Asin(βt +ϕ0 )

Предположим, что частота внешней силы не равна частоте собственных колебаний, т. е.

частное решение неоднородного уравнения (2.2) имеет вид

yн = P cosωt +Q sinωt ,

Подставляя эту функцию и вторую производную в уравнение (2.2), находим коэффициенты

P = 0, Q = q −aω2 .

(2.2)

(2.3)

(2.4)

β ≠ ω , тогда

(2.5)

P и Q :

Следовательно,			a
y	н	=	a	sinωt .		(2.6)
y		=	q −ω2	sinωt .		(2.6)
			q −ω2
Общее решение уравнения (2.2) определяется формулой y = yо + yн , т. е.
y = Asin(βt +ϕ0 ) +				a	sinωt .	(2.7)
y = Asin(βt +ϕ0 ) +				q −ω2	sinωt .	(2.7)
				q −ω2

Если частота собственных колебаний совпадает с частотой внешней силы, т. е. β = ω , то частное решение уравнения (2.2) следует искать в следующем виде:

			yн =t (P cosωt +Q sinωt) .				(2.8)
Подставляя функцию (2.8) и ее вторую производную в уравнение (2.2), находим
	a		~		a
P = −		,	Q = 0, т. е. y	= −		t cosωt .
	2ω				2ω

Итак, общее решение уравнения (2.2) в этом случае имеет вид y = Asin(βt +ϕ0 ) − 2aω t cosωt , или

y = Asin(βt +ϕ0 ) −	a	t cos βt ,	(2.9)
	2β

поскольку ω = β .

Из последней формулы видно (см. второе слагаемое алгебраической суммы), что амплитуда колебания неограниченно возрастает при неограниченном возрастании времени t . Рассматриваемое явление (частота собственных колебаний совпадает с частотой внешней силы) называется резонансом.

При выполнении условий p ≠ 0 и p42 < q характеристическое уравнение k2 + pk + q = 0 имеет ком- плексно-сопряженные корни k1 =α +iβ, k2 =α −iβ .

Общее решение однородного уравнения y′′+ p y′+ q y = 0 , где y = y(t) , определяется формулой

= eαt (C

cos βt +C

sin βt) или y

= Aeαt

sin(βt +ϕ

) .

(2.10)

Частное решение неоднородного уравнения (2.1) ищем в виде функции

yн = P cosωt +Q sinωt .

(2.11)

Подставляя функцию (2.11) и ее производные yо′, yо′′

в уравнение (2.1), находим коэффициенты P и Q:

P =

− pωa

Q =

(q −ω2 )a

(2.12)

(q −ω

)

(q −ω

)

+ p

+ p ω

Вводим новые постоянные величины

A1 и ϕ1 , полагая

P = A1 sinϕ1,

Q = A1 cosϕ1 ,

(2.13)

, tgϕ =

A = P2 +Q2

(q −

ω2 )2 + p2ω2

Формула (2.11) с учетом равенств (2.12) и (2.13) принимает вид

yн =

sin(ωt +ϕ1) .

(2.14)

(q −ω

2 )2

+ p2ω2

Общее решение уравнения (2.1) определяется формулой y = yо + yн

или

y = Aeαt sin(βt +ϕ

) +

sin(ωt +ϕ ) .

(2.15)

(q −ω2 )2 + p2ω2

Таким образом, отклонение y состоит из суммы двух слагаемых. Первое из них (решение соответствующего однородного уравнения) определяет затухающие колебания (α = − 2p < 0, ибо p > 0) , это слагаемое убывает

при возрастании t. Следовательно, через некоторый промежуток времени главное значениеy будет определяться вторым слагаемым, представляющим вынужденные колебания. Частотаω этих колебаний равна частоте внешней

силы: f (t) = asinωt . Амплитуда вынужденных колебаний тем больше, чемменьше p и разность q −ω2 .

<<< < Предыдущая 1 23 / 63 4 5 6 > Следующая >>>

Соседние файлы в предмете Высшая математика

#
19.02.2024626.04 Кб8ДифУр-яЧ1-1.pdf
#
19.02.2024449.07 Кб6ДифУр-яЧ1-2.pdf
#
19.02.20241 Mб2Контрольная работа Вариант С.doc
#
19.02.202457.97 Кб0Работа над ошибками Контрольная работа Вариант С.docx
#
19.02.2024707.21 Кб1РядыЧ-1.pdf