
Работа над ошибками Контрольная работа Вариант С
.docxНайти наибольшее и наименьшее значения функции
z(x, y)
= 5 + 8xy + 5
+ 8xy + 5 – 18x – 18y
– 18x – 18y
в замкнутой области Ω, заданной системой неравенств 0 ≤ x ≤ 2, 0 ≤ y ≤ 3. Сделать чертеж.
 = 10x + 8y – 18
= 10x + 8y – 18
 = 8x + 10y – 18
= 8x + 10y – 18






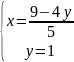

 (1;
1) ∈ Ω
(1;
1) ∈ Ω
z( ) = 5 + 8 + 5 – 18 – 18 = -18
y = 0, z = 5 – 18x
 = 10x – 18 = 0
= 10x – 18 = 0
5x – 9 = 0
x =
 ∈ [0; 2]
∈ [0; 2]
 (
;
0) ∈ Ω
(
;
0) ∈ Ω
z(
)
= 5 *
 – 18 *
= -
– 18 *
= -
 (0;
0) ∈ Ω
(0;
0) ∈ Ω
z( ) = 0
 (2;
0) ∈ Ω
(2;
0) ∈ Ω
z(
)
= 5 *
 – 18 * 2 = -16
– 18 * 2 = -16
y = 3, z = 5
+ 8 * 3 * x + 5 *
 – 18x – 18 * 3 = 5
+ 6x – 9
– 18x – 18 * 3 = 5
+ 6x – 9
= 10x + 6 = 0
5x + 3 = 0
x = - ∉ [0; 2]
∉ [0; 2]
 (0;
3) ∈ Ω
(0;
3) ∈ Ω
z( ) = -9
 (2;
3) ∈ Ω
(2;
3) ∈ Ω
z( ) = 5 * + 6 * 2 – 9 = 23
x = 0, z = 5 – 18y
= 10y – 18 = 0
5y – 9 = 0
y = ∈ [0; 3]
 (0;
)
∈ Ω
(0;
)
∈ Ω
z( ) = 5 * – 18 * = -
x = 2, z = 5 * + 8 * 2 * y + 5 – 18 * 2 – 18y = 5 – 2y – 16
= 10y – 2 = 0
5y – 1 = 0
y =
 ∈ [0; 3]
∈ [0; 3]
 (2;
)
∈ Ω
(2;
)
∈ Ω
z(
)
= 5 *
 – 2 *
– 16 = -
– 2 *
– 16 = -
 = z(
)
= -18
= z(
)
= -18
 = z(
)
= 23
= z(
)
= 23

Вычислить криволинейный интеграл
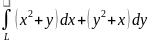 ,
,
где L – ломаная линия, состоящая из отрезков прямых x = 5 и y = 1, от точки A(2; 1) до точки B(5; 3).

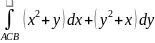 =
=
 +
+

AC: y = 1, dy = 0
=
 =
=
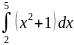 = (
= ( + x)
+ x) = =
= =
 –
–
 + 5 – 2 = 42
+ 5 – 2 = 42
CB: x = 5, dx = 0
=
 =
=
 = (
= ( + + 5y)
+ + 5y) = 9 –
= 9 –
 + 15 – 5 =
+ 15 – 5 =

= 42 +
=

