
1.1 пример задачи Статика
.pdf
1.В задаче требуется рассмотреть вал, находящийся в равновесии. Вал-это железная ось между цилиндрическим шарниром А и шкивом (колесом) 3. На валу закреплены шкивы (колеса) 1,2,3.
2.
А иВ –Цилиндрические шарниры, они не дают валу упасть вниз. То ,что мешает свободно перемещаться телу в пространстве(падать вниз под действием силы тяжести в нашем случае) называется связями.
3.Связи, можно мысленно отбросить для решения задачи, заменив их силами реакции связей(принцип освобождаемости от связей).Подробней про связи есть в лекциях.
4.Силы реакции связей направлены в сторону ,противоположную той, куда связь не дает перемещаться телу. В нашей задаче это направление перпендикулярное оси вала. Как именно, мы не знаем, поэтому,
1
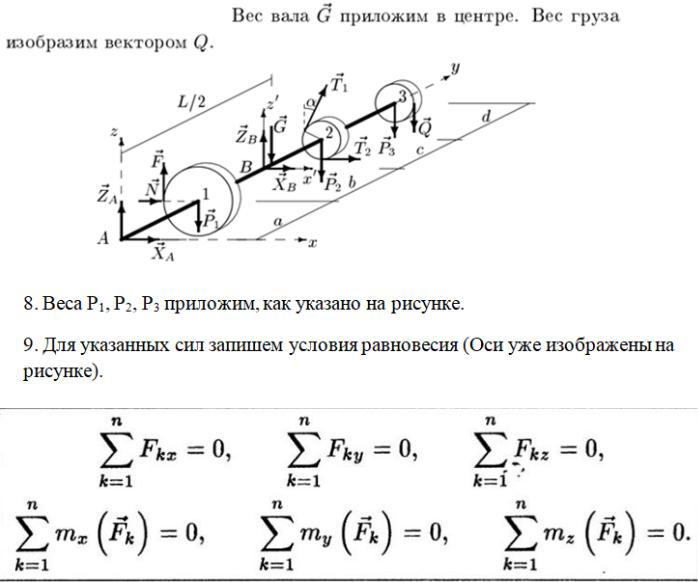
раскладываем их на две составляющие XA и ZA – составляющие силы реакции
шарнира A . Для шарнира В аналогично.
5.На рисунке :а- это расстояние от шарнира А до шкива 1, b – между шкивом 1 и
шарниром В, с- между В и 2, d-между 2 и 3.
6.Нарисуем новую картинку , указав все приложенные силы
7.
10. . В условиях равновесия ,записанных в рамке, три первых суммыэто суммы прекций сил на оси X,Y,Z.
11. Запишем первое равенство-спроектируем каждую силу на ось X и просуммируем прекции ,приравняв сумму к нулю.
2

При проектировании учтем взаимное расположение векторов сил и осей, чтобы указать нужный знак + или - .
12. Т.к. все силы лежат в плоскостях перпендикулярных оси вала, и следовательно оси Y , то проекция каждой из сил на ось Y равна 0.
Второе равенство получается 0 = 0.
13. Запишем третье равенство
Сумма проекций векторов сил на ось Z.
14.Еще три уравненияэто суммы моментов сил относительно осей X,Y,Z.
15.Алгоритм вычисления момента силы F относительно оси :
3

16. Будем вычислять моменты сил относительно оси X . Согласно п.15 мы должны каждую из сил спроектировать на плоскость перпендикулярную оси X. В качестве такой плоскости возьмем плоскость ZAY.
Чтобы было понятней, нарисуем вспомогательный рисунок - вид сбоку, т.е. как мы видим плоскость ZAY c положительного направления оси X. Укажем на рисунке проекции всех сил.
17. Теперь вычислим моменты , умножая длину проекции на плечо (расстояние от точки А до линии действия проекции) ,затем их все просуммируем. Если проекция пытается совершить поворот против часовой стрелки вокруг точки А (смотрим в направлении стрелки) , то момент со знаком +, если против ,то - .
Момент силы Za равен 0 ,т.к. расстояние от точки А до линии действия силы 0.
18. Запишем следующее равенство нулю суммы моментов сил относительно оси Y.
Нарисуем вспомогательную картинку для проекций всех сил на плоскость перпендикулярную оси Y – это плоскость ZAX. Шкив 2 нарисован пунктиром т.к. его
4

радиус меньше, чем радиус шкива 3 и если мы смотрим с положительного направления оси Y, то он нам не виден из-за шкива 3.
Тогда
Моменты сил, проекции которых проходят через центр А равны нулю так как плечо равно нулю.
5
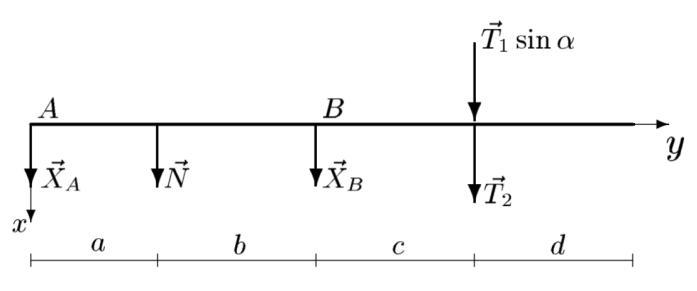
19. Запишем третье уравнение, найдя сумму моментов относительно оси Z. Нарисуем дополнительную картинку:
20.В полученные шесть равенств, одно из которых нулевое, подставим числа, данные в условии. Получим пять уравнений с пятью неизвестными. Решая эти уравнения, найдем искомые неизвестные.
21.Конечным результатом, достаточным для получения зачета по данной теме, должна быть система уравнений с пятью неизвестными (верно записанные условия равновесия пространственной системы сил). Числовые значения находить не требуется.
6
