Контрольная работа / Контрольная работа по теоретической механике(Вариант С)
.docxЗадание Статика, вариант С.
Равновесие вала
Горизонтальный вал весом G=20Н может вращаться в цилиндрических шарнирах A и B. К шкиву 1 приложено нормальное давление N и касательная сила сопротивления F=0,3N. На шкив 2 действуют силы натяжения ремней T1=40Н и T2=24Н. Груз Q=10Н висит на нити, навитой на шкив 3. Определить силу давления N и реакции шарниров в условии равновесия вала. Учесть веса шкивов P1=44Н, P2=30Н, P3=38Н. Все нагрузки действуют в вертикальной плоскости (см. рис. 1). Размеры вала а=24см; b=25см; c=28см; d=27см. Размеры шкивов R1=16см, R2=10см, R3=12см. Угол наклона ⍺=600.

Рисунок 1 – Исходная схема нагрузки вала
Решение.
1.
Вал в пространстве вращается равномерно.
Равновесие системы обеспечивает сила
 .
Нанесем вес шкивов
.
Нанесем вес шкивов
 ,
,
 и
и
 ,
численные значения длин. Вал
вращается на двух цилиндрических опорах
(подшипниках) в точках А
и В.
В обеих опорах будет по две составляющие
реакции вдоль осей х
и z
(см. рис. 2). Пусть направление составляющих
реакций совпадает с положительным
направлением осей. Уточнять направление
реакций будем после решения уравнений.
,
численные значения длин. Вал
вращается на двух цилиндрических опорах
(подшипниках) в точках А
и В.
В обеих опорах будет по две составляющие
реакции вдоль осей х
и z
(см. рис. 2). Пусть направление составляющих
реакций совпадает с положительным
направлением осей. Уточнять направление
реакций будем после решения уравнений.

,,
Рисунок 2 – Расчетная схема нагрузки вала к определению неизвестных усилий
Имеем 5 неизвестных: сила и 4 реакции, составим 5 уравнений равновесия:










Решаем относительно искомых неизвестных:









Действительное
направление реакций совпадают с
предложенным направлением
на расчетной схеме, кроме
 .
Изменим ее направление на противоположное
(см. рис. 2).
.
Изменим ее направление на противоположное
(см. рис. 2).
Ответы;


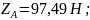


Кинематика. Задача 3, вариант С.
КИНЕМАТИКА МАТЕРИАЛЬНОЙ ТОЧКИ
Материальная
точка движется в плоскости ху.
Закон движения точки задан уравнениями:
 и
и
 ,
где
х
и у
в см.
t
в секундах.
,
где
х
и у
в см.
t
в секундах.
Найти уравнение траектории точки (изобразить траекторию на чертеже). Для момента времени t1=2 c определить: 1) скорость точки, 2) ускорение точки, 3) касательное ускорение точки, 4) нормальное ускорение точки, 5) радиус кривизны в соответствующей точке траектории.
Решение.
1. Для определения уравнения траектории точки исключим из заданных уравнений движения время t. Поскольку t входит в аргументы тригонометрических функций, то выделим из обоих уравнений квадраты функций и сложим левые и правые части уравнений:


__________________

Преобразуем уравнение и получим:

Траектория прямая линия. Чтобы построить прямую линию достаточно иметь координаты двух точек. Определим точки пересечения прямой линии с осями координат и построим траекторию движения точки (см. рис. 3):
- пересечение линии с осью х:

- пересечение линии с осью у:
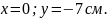

Рисунок 3 – К определению абсолютной скорости и абсолютного ускорения и других кинематических параметров точки в заданный момент времени
2.
Определим положение материальной точки
на траектории в момент времени t1
=
 с
и построим его (см. рис. 3).
с
и построим его (см. рис. 3).


3. Определим абсолютную скорость точку в рассматриваемый момент времени.
3.1. Определим составляющую скорости вдоль оси х, как первую производную координаты х по времени:

В заданный момент времени:

Направление
вектора
 совпадает с положительным направлением
оси х.
совпадает с положительным направлением
оси х.
3.2. Определим составляющую скорости вдоль оси у, как первую производную координаты у по времени:

В заданный момент времени:

Направление
вектора
 совпадает с положительным направлением
оси у.
совпадает с положительным направлением
оси у.
3.3. Абсолютная скорость точки в заданный момент времени определим на основании теоремы Пифагора:

Направление
вектора
 абсолютной скорости определим по
правилу параллелограмма (см. рис. 3).
Проверка: абсолютная скорость точки
при прямолинейном движении должна быть
направлена вдоль прямолинейной
траектории.
абсолютной скорости определим по
правилу параллелограмма (см. рис. 3).
Проверка: абсолютная скорость точки
при прямолинейном движении должна быть
направлена вдоль прямолинейной
траектории.
4. Определим абсолютное ускорение точки в рассматриваемый момент времени.
4.1.
Определим составляющую ускорения вдоль
оси х,
как первую производную скорости
 по времени:
по времени:

В заданный момент времени:

Направление
вектора
 не совпадает с положительным направлением
оси х.
не совпадает с положительным направлением
оси х.
4.2. Определим составляющую скорости вдоль оси у, как первую производную координаты у по времени:

В заданный момент времени:
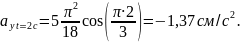
Направление
вектора
 не совпадает с положительным направлением
оси y.
не совпадает с положительным направлением
оси y.
4.3. Модуль абсолютного ускорения точки в заданный момент времени определим на основании теоремы Пифагора:

Направление
вектора
 абсолютного ускорения определим по
правилу параллелограмма (см. рис. 3).
Проверка: абсолютное ускорение точки
при прямолинейном движении должна быть
направлена вдоль прямолинейной
траектории.
абсолютного ускорения определим по
правилу параллелограмма (см. рис. 3).
Проверка: абсолютное ускорение точки
при прямолинейном движении должна быть
направлена вдоль прямолинейной
траектории.
4.4. Определим модуль касательного ускорения по формуле:

Направление
вектора
 касательного ускорения прямолинейного
движения совпадает с
на линию действия абсолютной скорости
(см. рис. 3), но направлению скорости
противоположно – движение замедленное.
касательного ускорения прямолинейного
движения совпадает с
на линию действия абсолютной скорости
(см. рис. 3), но направлению скорости
противоположно – движение замедленное.
4.5. Определим модуль нормального ускорения по формуле:
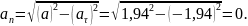
5. Определим радиус кривизны траектории в рассматриваемой точке траектории:
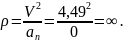
Действительно – траектория движения прямая линия.
Кинематика. Задача 4, вариант С.
Точка
М
движется в направляющей трубке АВ
по закону
 .
В начальный момент времени положение
точки М
совпадает с точкой О.
Положение точки М
на рисунке 4 соответствует положительному
значению координаты s.
Трубка АВ
совершает вращательное движение по
закону
.
В начальный момент времени положение
точки М
совпадает с точкой О.
Положение точки М
на рисунке 4 соответствует положительному
значению координаты s.
Трубка АВ
совершает вращательное движение по
закону
 ,
положительное направление вращения
см. рис. 4.
,
положительное направление вращения
см. рис. 4.

Рисунок 4 - Исходная схема сложного движения точки М
Для момента времени t=t1=1c определить абсолютную скорость и абсолютное ускорение точки М.
Решение.
1.1. Выделим каждое движение и дадим наименование.
- трубка АВ для движения материальной точки М связана с подвижной системой отсчета. Движение точки М относительно подвижной системы отсчета называется относительным. Все параметры, связанные с этим движением будут отмечаться индексом r;
- ось вращающегося О1О2 круга, с расположенной на нем трубкой АВ, связана с неподвижной системой отсчета. Их движение относительно неподвижной системы отсчета называется переносным. Все параметры, связанные с этим движением будут отмечаться индексом е;
- движение материальной точки М относительно неподвижной системы отсчета называется абсолютным. Все параметры, связанные с этим движением будут отмечаться индексом а.
2. Определим положение точки М в заданный момент времени.
2.1. Выделим относительное и переносное движение.
- будем считать, что в заданный момент времени переносное движение (плоскость круга) совпадает с плоскостью чертежа.
- движение точки М по трубке АВ – относительное движение. Определим длину дуги ОМ, пройденную точкой М за время t1=1c:

2.2.
Выполним расчётную схему с уточненным
положением точки М
в трубке для последующего нанесения
скоростей или ускорений (см. рис. 5).
Координата ОМ
увеличивается, так как получили
 .
.

Рисунок 5 – Определение абсолютной скорости точки М
3. Определим абсолютную скорость точки М, как геометрическую сумму относительной и переносной скоростей.
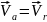 +
+
3.1. Определим относительную скорость:
- модуль относительной скорости определим как первую производную перемещения по времени:


-направление
 в направлении увеличения координаты
ОМ
в направлении увеличения координаты
ОМ
3.2. Определим переносную скорость:
- модуль переносной скорости точки М определим через переносную угловую скорость тела D, которую определим как первую производную угла поворота по времени:


-так
как величина
 ,
то направление вращения
,
то направление вращения
 совпадает
с направлением увеличения угла поворота
совпадает
с направлением увеличения угла поворота
 .
.
- модуль переносной скорости точки М определим по формуле:

где
 – радиус переносного движения (см. рис.
5), измеряется, как расстояние от точки
М
до оси вращения О1О2
и численно равен:
– радиус переносного движения (см. рис.
5), измеряется, как расстояние от точки
М
до оси вращения О1О2
и численно равен:


Вектор
 направлен в сторону вращения
,
перпендикулярно плоскости чертежа.
направлен в сторону вращения
,
перпендикулярно плоскости чертежа.
3.3. Определим абсолютную скорость точки М по теореме Пифагора. Угол между скоростями 900, потому что вектор лежит в плоскости чертежа, а вектор перпендикулярен чертежу.

Направление
вектора
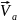 абсолютной
скорости по правилу параллелограмма
(см. рис. 5).
абсолютной
скорости по правилу параллелограмма
(см. рис. 5).
3. Определим абсолютное ускорение точки М, как геометрическую сумму относительного, переносного ускорения и ускорения Кориолиса (см. рис. 6).

Рисунок 6 – Определение абсолютного ускорения точки М

3.1. Определим относительное ускорение. Так как относительное движение прямолинейное, определим его, как первую производную относительно скорости по времени:

от времени не зависит;
-направление
вектора
 совпадает с направлением скорости
так
как имеют одинаковые знаки.
совпадает с направлением скорости
так
как имеют одинаковые знаки.
3.2. Определим переносное ускорение.
Так как переносное движение вращательное, имеет две составляющие – вращательную и центробежную.

-модуль вращательной составляющей ускорения определим через переносное угловое ускорение, которое определим, как первую производную угловой скорости по времени:

в рассматриваемый момент времени:

-так
как величина
 ,
то направление вращения
,
то направление вращения
 совпадает
с направлением вращения
совпадает
с направлением вращения
 ;
;
- модуль переносного вращательного ускорения точки М определим по формуле:

-
направление вектора
 совпадает с направлением
, так как имеют одинаковые знаки.
совпадает с направлением
, так как имеют одинаковые знаки.
-центробежная составляющая ускорения по величине:

- направление по радиусу Re от точки М к оси вращения.
3.3. Ускорение Кориолиса:
- модуль определим по формуле:

Так
как
 направлена вдоль оси вращения переносного
движения по О1О2
вверх, а
направлена к точке А, вверх, по прямой
АВ, составляющей с осью вращения угол
300.
Значит,
направлена вдоль оси вращения переносного
движения по О1О2
вверх, а
направлена к точке А, вверх, по прямой
АВ, составляющей с осью вращения угол
300.
Значит,
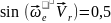 .
Тогда
.
Тогда

-
направление вектора
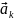 ускорения
Кориолиса по правилу Н. Е. Жуковского
(см. рис. 7):
ускорения
Кориолиса по правилу Н. Е. Жуковского
(см. рис. 7):

Рисунок 7 – Правило Н. Е. Жуковского для определения направления ускорения Кориолиса
3.4. Определим абсолютное ускорение точки М методом проекций. Для этого построим оси координат xyz и далее по теореме Пифагора.




Задача 6, вариант С.
 Шарик
массы m=0,6кг
движется из положения А
внутри изогнутой трубки, расположенной
в вертикальной плоскости (см. рис. 8).
Шарик, пройдя путь lо=20см,
отделяется от пружины. В точке В
шарик, не меняя своей скорости, переходит
на участок ВС,
где на него дополнительно действует
сила
Шарик
массы m=0,6кг
движется из положения А
внутри изогнутой трубки, расположенной
в вертикальной плоскости (см. рис. 8).
Шарик, пройдя путь lо=20см,
отделяется от пружины. В точке В
шарик, не меняя своей скорости, переходит
на участок ВС,
где на него дополнительно действует
сила
 =0.
(направление указано на рис. 8). Пользуясь
общими уравнениями динамики, определить
скорость точки в положениях B
и С.
=0.
(направление указано на рис. 8). Пользуясь
общими уравнениями динамики, определить
скорость точки в положениях B
и С.
Рисунок 8 – Заданная схема движения шарика
Исходные данные: начальная скорость шарика VA=0;
длина участка АВ=0,5м;
время движения на участке ВС τ=1,2с;
коэффициент трения скольжения f=0,12;
коэффициент жесткости пружины с=1,9Н/см;
угол наклона трубки ⍺=450.
Решение.
1. Составим расчетную схему.
1.1. Добавим точку D – отделение шарика от пружины.
1.2.
Рассмотрим действующие на шарик силы
при его движении на участке АD:
силы
 ,
и
,
и
 тр;
упр
(см. рис. 9). Известна длина участка АD,
равная l0.
тр;
упр
(см. рис. 9). Известна длина участка АD,
равная l0.
Для решения используем теорему об изменении кинетической энергии:

где
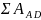 – сумма работ сил, действующих на
рассматриваемом участке.
– сумма работ сил, действующих на
рассматриваемом участке.

Рисунок 9 – Расчетная схема к определению искомых величин

 – так
как эта сила не совершает работу –
перпендикулярна к направлению движения
шарика.
– так
как эта сила не совершает работу –
перпендикулярна к направлению движения
шарика.
 -
работа силы тяжести при изменении высоты
на величину h,
которая равна:
-
работа силы тяжести при изменении высоты
на величину h,
которая равна:


 – работа
силы трения.
– работа
силы трения.

 – работа
силы упругости пружины.
– работа
силы упругости пружины.

Подставим все в теорему об изменении кинетической энергии

или


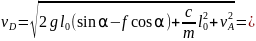

2. Составим расчетную схему с нанесением всем действующих сил , и тр при движении шарика на участке DB (см. рис. 9). На участке DВ известна длина участка, равная АВ-l0=0,5-0,2=0,3м.
Для решения используем теорему об изменении кинетической энергии:

где
 – сумма работ сил, действующих на
рассматриваемом участке.
– сумма работ сил, действующих на
рассматриваемом участке.

– так как эта сила не совершает работу – перпендикулярна к направлению движения шарика.
 -
работа силы тяжести при изменении высоты
на величину h2,
которая равна:
-
работа силы тяжести при изменении высоты
на величину h2,
которая равна:
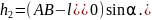

– работа силы трения.

Подставим все в теорему об изменении кинетической энергии:

или



3.
Составим расчетную схему с нанесением
всем действующих сил
,
и
тр
при
 для движении шарика на участке BС
(см.
рис. 9).
для движении шарика на участке BС
(см.
рис. 9).
Для решения используем теорему об изменении количества движения:

где
 – сумма импульсов всех сил, действующих
на шарик при движении на участке BС.
– сумма импульсов всех сил, действующих
на шарик при движении на участке BС.
Рассмотрим импульсы трех действующих сил в проекции:




Подставим в теорему об изменении количества движения:

или
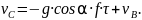
Подставим значения и определим скорость в точке С: