
- •1. Численное интегрирование системы дифференциальных уравнений. Явный и неявный методы Эйлера.
- •2. Получение синтетической схемы, заменяющей катушку, конденсатор.
- •3. Пример использования метода синтетических схем для расчёта переходного процесса.
- •4. Макромодели.
- •5. Переходная и импульсная характеристики цепи.
- •6. Пример расчёта переходной и импульсной характеристики для цепи 1-го порядка
- •7. Интеграл Дюамеля. Пример расчёта цепи с помощью интеграла Дюамеля.
- •8. Решётчатые функции. Переход от функции непрерывного времени к решетчатой функции.
- •9.Разностные уравнения 1-го порядка. Пример формирования разностного уравнения для цепи, находящейся под воздействием последовательности прямоугольных импульсов.
- •10. Формирование разностного уравнения для цепи 1-го порядка, находящейся под воздействием последовательности δ- импульсов.
- •Примеры z-изображений решетчатых функций.
- •12. Решение разностного уравнения методом z- преобразования. Переход от z–изображения к оригиналу (решетчатой функции).
- •13. Расчёт переходного процесса методом z- преобразования с использованием передаточной функции импульсной системы (в случае прямоугольных импульсов и δ-импульсов).
- •14. Резонансные частоты цепи, состоящей из двух индуктивно связанных контуров.
- •15. Частотные характеристики цепи, состоящей из двух индуктивно связанных контуров.
- •16. Общие свойства входных функций цепей, содержащих только реактивные элементы.
- •17. Пример построения частотных характеристик цепей, содержащих только реактивные элементы.
- •18. Устойчивость в цепи с нелинейным элементом и индуктивностью
- •19. Устойчивость в цепи с нелинейным элементом и ёмкостью.
- •20. Релаксационные колебания.
17. Пример построения частотных характеристик цепей, содержащих только реактивные элементы.
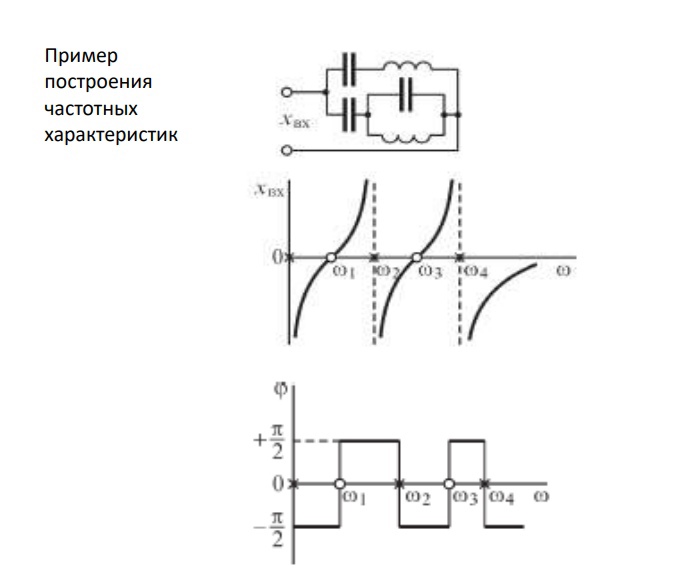
Теория:
Запишем выражение для входного сопротивления xвх пассивного двухполюсника, содержащего только реактивные элементы:

где:
 - корни полинома числителя;
– корни полинома знаменателя.
- корни полинома числителя;
– корни полинома знаменателя.
В цепи, содержащей только реактивные
элементы, угол сдвига φ между напряжением
и током может принимать только значения
 .
При резонансе в таких цепях φ = 0, поэтому
в момент резонанса в цепи (частота ω
равна корню одного из полиномов)
происходит скачкообразное изменение
угла φ от
.
При резонансе в таких цепях φ = 0, поэтому
в момент резонанса в цепи (частота ω
равна корню одного из полиномов)
происходит скачкообразное изменение
угла φ от
 до
до
 .
.
В этих точках (точках резонанса, частота
ω равна корню одного из полиномов)
 (нуль, если корень полинома числителя)
или
(нуль, если корень полинома числителя)
или
 (полюс, если корень полинома знаменателя).
(полюс, если корень полинома знаменателя).
Для чисто реактивных цепей x(ω)
всегда возрастает с ростом ω. На втором
графике видно, что xвх
увеличивается от
 (полюс), растет, проходя через нуль и
возрастая далее, снова проходит через
полюс
(полюс), растет, проходя через нуль и
возрастая далее, снова проходит через
полюс
 ,
процесс затем повторяется.
,
процесс затем повторяется.
Когда
 ,
,
 ,
,

Когда
 ,
,
 ,
,

Это видно из формул
 ,
,

Теперь рассмотрим данную схему:
На пути от одного входного зажима к другому имеется цепочка ветвей, состоящая только из конденсаторов.
При
,
 (катушки превращаются в разрыв, а
конденсаторы – в провод).
(катушки превращаются в разрыв, а
конденсаторы – в провод).
Получаем, что xвх стремится к 0 пропорционально 1/ω.
В точке ω = 0,
 ,
потому как должно всегда возрастать.
,
потому как должно всегда возрастать.
Строим второй график.
18. Устойчивость в цепи с нелинейным элементом и индуктивностью
Особенности колебательных процессов в нелинейных цепях: в линейных цепях при воздействии постоянных ЭДС установившимися могут быть только постоянные токи. В отличие от линейных цепей при воздействии постоянных ЭДС в нелинейной цепи установившимися могут быть не только постоянные токи, но и колебательные токи. Последние возникают вследствие возможности неустойчивых состояний в нелинейной цепи, причём амплитуда установившихся колебаний определяется нелинейными свойствами цепи.
Рисунок 18.1 – Цепь с нелинейным
элементом (дуга) и индуктивностью
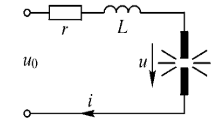
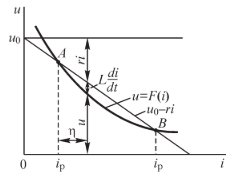
Рисунок 18.2 – График
зависимости u от i
Электрическая дуга обладает падающей характеристикой u=F(i), изображённой на рисунке 18.2. Уравнение цепи имеет вид:
![]() (*)
(*)
При равновесии в цепи ток не должен изменяться, т.е. должно быть di/dt = 0. Условимся обозначать величины при равновесии с индексом «р». На рисунке 18.2 проведена также прямая u0-ri. Равновесие имеет место при пересечении этой прямой с характеристикой дуги, т.е. в точках А и В. Выясним, какое из этих состояний будет устойчивым, а какое – неустойчивым. При равновесии имеем
![]() (**)
(**)
Пусть в некоторый момент времени, который примем за начальный (t=0), по какой-либо причине ток получил малое отклонение η0 от положения равновесия.
В следующие моменты времени это отклонение начнёт изменяться, т.е. будет функцией времени. Обозначим его через η. При этом ток будет равен:
![]()
Напряжение u на дуге можно выразить через его значение up при равновесии и через η, разлагая u=F (ip+ η) в ряд по степеням η. Отбрасывая в первом приближении члены с η во второй и более высоких степенях, получаем:
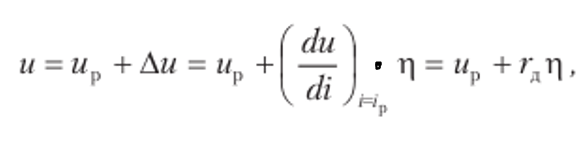
где
 -
динамическое сопротивление участка с
электрической дугой при i=ip.
-
динамическое сопротивление участка с
электрической дугой при i=ip.
Учитывая ещё, что di/dt = dη/dt и подставляя выражения i=iр+ η, di/dt и u в основное уравнение цепи (*), находим:
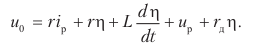
Вычитая отсюда уравнение равновесия (**), получаем уравнение для приращения тока η:
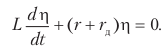
Это уравнение оказалось линейным, поскольку мы ограничились первым приближением, т. е. ограничились первым членом в разложении Δu по степеням η. Его характеристическое уравнение
![]()
Имеет единственный корень
![]()
И решение для η с учётом начального его значения имеет вид
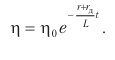
Если α <0, т.е. если (r+rд)>0, то η→0 при t→∞, т.е. ток i возвращается к его значению ip при равновесии.
Наоборот, при α >0, т.е. при (r+rд) <0, имеем η→∞ при t→0, т.е. величина i удаляется от её значения ip при равновесии.
Так как вследствие падающей характеристики
дуги
![]() то
условие (r+rд)>0
означает, что наклон прямой u0-ri
больше наклона кривой u=F(i),
что имеет место в точке В. Эта точка
является точкой устойчивого равновесия.
то
условие (r+rд)>0
означает, что наклон прямой u0-ri
больше наклона кривой u=F(i),
что имеет место в точке В. Эта точка
является точкой устойчивого равновесия.
Условие (r+rд)<0 означает, что наклон прямой u0-ri меньше наклона кривой u=F(i), что имеет место в точке А. Эта точка является точкой неустойчивого равновесия. Малейшее отклонение от неё ведёт либо к переходу в точку В, либо к погасанию дуги.
Таким образом, устойчивое состояние соответствует отрицательному корню характеристического уравнения, относящегося к линейному в первом приближении уравнению для отклонения η. Можно сказать также, что устойчивое состояние данной цепи характеризуется тем, что динамическое сопротивление (r+rд) всей цепи положительно.
