
- •1. Численное интегрирование системы дифференциальных уравнений. Явный и неявный методы Эйлера.
- •2. Получение синтетической схемы, заменяющей катушку, конденсатор.
- •3. Пример использования метода синтетических схем для расчёта переходного процесса.
- •4. Макромодели.
- •5. Переходная и импульсная характеристики цепи.
- •6. Пример расчёта переходной и импульсной характеристики для цепи 1-го порядка
- •7. Интеграл Дюамеля. Пример расчёта цепи с помощью интеграла Дюамеля.
- •8. Решётчатые функции. Переход от функции непрерывного времени к решетчатой функции.
- •9.Разностные уравнения 1-го порядка. Пример формирования разностного уравнения для цепи, находящейся под воздействием последовательности прямоугольных импульсов.
- •10. Формирование разностного уравнения для цепи 1-го порядка, находящейся под воздействием последовательности δ- импульсов.
- •Примеры z-изображений решетчатых функций.
- •12. Решение разностного уравнения методом z- преобразования. Переход от z–изображения к оригиналу (решетчатой функции).
- •13. Расчёт переходного процесса методом z- преобразования с использованием передаточной функции импульсной системы (в случае прямоугольных импульсов и δ-импульсов).
- •14. Резонансные частоты цепи, состоящей из двух индуктивно связанных контуров.
- •15. Частотные характеристики цепи, состоящей из двух индуктивно связанных контуров.
- •16. Общие свойства входных функций цепей, содержащих только реактивные элементы.
- •17. Пример построения частотных характеристик цепей, содержащих только реактивные элементы.
- •18. Устойчивость в цепи с нелинейным элементом и индуктивностью
- •19. Устойчивость в цепи с нелинейным элементом и ёмкостью.
- •20. Релаксационные колебания.
Примеры z-изображений решетчатых функций.
 Таблица
11.1 – Примеры z-изображений решетчатых
функций.
Таблица
11.1 – Примеры z-изображений решетчатых
функций.




Обратное z-преобразование

(Полюс функции – это точка, где предел функции равен бесконечности).

12. Решение разностного уравнения методом z- преобразования. Переход от z–изображения к оригиналу (решетчатой функции).
Метод z-преобразования можно применить к решению разностного уравнения цепи. В этом случае получение разностного уравнения является промежуточным этапом решения задачи. Ниже рассмотрен уже знакомый пример для RL цепи. Если непонятно, откуда взялись все эти формулы, то их вывод расписан в предыдущих вопросах.



13. Расчёт переходного процесса методом z- преобразования с использованием передаточной функции импульсной системы (в случае прямоугольных импульсов и δ-импульсов).




Рассмотрим расчёт тока в r-L цепи при воздействии на её вход последовательности δ-импульсов напряжения площадью К[n].
1 способ: применим z – преобразование для решения разностного уравнения цепи
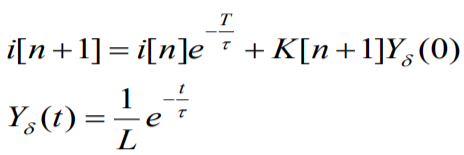
z - изображение разностного уравнения:
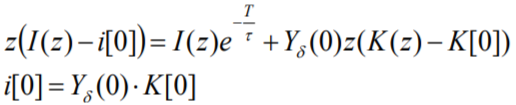
Считаем, что все импульсы имеют одинаковую площадь К. Тогда z-изображение последовательности площадей δ – импульсов K[n]:
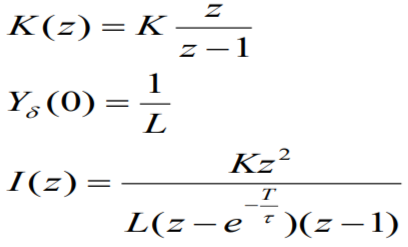
Переход к оригиналу:
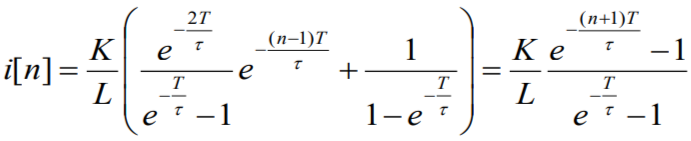
2-й способ: с помощью передаточной функции при воздействии δ – импульсов Hδ(z). Если Xвх(z) =1, т.е. является z-изображением одиночного δ -импульса единичной площади, то Xвых(z) = Нδ(z) – z-изображение реакции цепи на воздействие одиночного δ -импульса единичной площади hδ[n], где hδ[n]=hδ(nT).
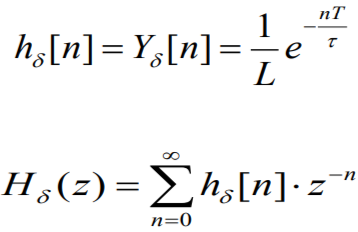
Находим сумму ряда:
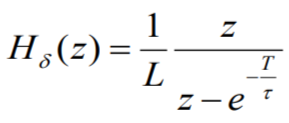
Z-изображение тока:
![]()
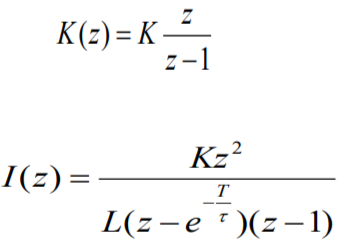
z-изображение тока аналогично изображению, полученному при решении разностного уравнения.
14. Резонансные частоты цепи, состоящей из двух индуктивно связанных контуров.
Реактивные сопротивления и проводимости отдельных участков цепи могут быть как положительными, так и отрицательными величинами и, следовательно, могут взаимно компенсироваться. Поэтому возможны случаи, когда, несмотря наличие в цепи индуктивных катушек и конденсаторов, входное реактивное сопротивление или входная реактивная проводимость всей цепи оказываются равными нулю. При этом ток и напряжение на входе цепи совпадают по фазе, и эквивалентное сопротивление всей цепи будет активным. Такое явление называют резонансным.
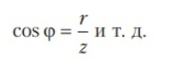 Выясним
характерные черты этого явления и его
связь с так называемыми частотными
характеристиками на некоторых частных
случаях, понимая под частотными
характеристиками зависимости от частоты
параметров цепи (r, x,
z, g, b,
y), а также величин,
определяемых параметрами.
Выясним
характерные черты этого явления и его
связь с так называемыми частотными
характеристиками на некоторых частных
случаях, понимая под частотными
характеристиками зависимости от частоты
параметров цепи (r, x,
z, g, b,
y), а также величин,
определяемых параметрами.
Резонанс и частотные характеристики
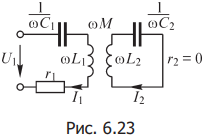
Рис. 14.1.
Определим резонансные частоты и частотные характеристики в цепи, изображённой на рис. 14.1.
Д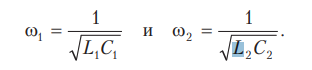 ля
упрощения расчёта пренебрежём активным
сопротивлением вторичного контура.
Собственные частоты контуров, при
которых в них наступает резонанс, в
случае отсутствия взаимной индукции
равны:
ля
упрощения расчёта пренебрежём активным
сопротивлением вторичного контура.
Собственные частоты контуров, при
которых в них наступает резонанс, в
случае отсутствия взаимной индукции
равны:
И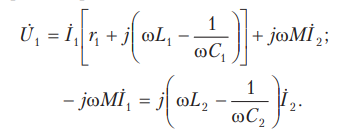
 меем
уравнения рассматриваемой цепи:
меем
уравнения рассматриваемой цепи:
Условие резонанса напряжений – равенство
нулю эквивалентного реактивного
сопротивления, т.е. x1э=0,
откуда
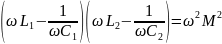 .
.
Разделив на
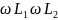 обе части этого выражения, получим
обе части этого выражения, получим
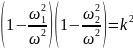
Формула коэффициента связи:
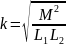

При частотах
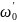 и
и
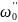 сопротивление цепи оказывается
минимальным и равным r1,
а ток I1 достигает
максимальных значении: I1
= U1/r1.
сопротивление цепи оказывается
минимальным и равным r1,
а ток I1 достигает
максимальных значении: I1
= U1/r1.
При
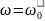 имеем x1э = ∞ и ток I1
= 0. Это можно пояснить следующим образом:
при частоте
имеем x1э = ∞ и ток I1
= 0. Это можно пояснить следующим образом:
при частоте
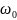 имеет место резонанс во вторичном
контуре х2 =
имеет место резонанс во вторичном
контуре х2 =
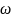 L2-1/(
С2) = 0 , и при условии r2
= 0 получается z2 = 0.
Как видно из уравнения для второго
контура, при конечном значении тока
L2-1/(
С2) = 0 , и при условии r2
= 0 получается z2 = 0.
Как видно из уравнения для второго
контура, при конечном значении тока
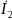 ЭДС взаимной индукции
ЭДС взаимной индукции
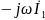 должна быть равна нулю, т. е. I1
= 0. Ток
устанавливается таким, чтобы ЭДС взаимной
индукции
должна быть равна нулю, т. е. I1
= 0. Ток
устанавливается таким, чтобы ЭДС взаимной
индукции
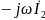 со стороны второго контура уравновесила
приложенное к первому контуру напряжение,
что видно из первого уравнения при I1
= 0. Этот случай по своему характеру
аналогичен резонансу токов в контуре
без потерь.
со стороны второго контура уравновесила
приложенное к первому контуру напряжение,
что видно из первого уравнения при I1
= 0. Этот случай по своему характеру
аналогичен резонансу токов в контуре
без потерь.
Н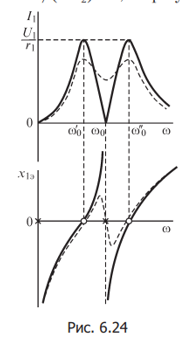 а
рис. 6.24 представлена частотная
характеристика I1(ω)
при U1 = const, а также частотная
характеристика х1э(ω). Полюсами
функции х1э(ω) являются частоты
ω=0, ω=ω0 и ω=∞. Ее нулями являются
частоты ω=
и ω=
.
Во всем диапазоне частот соблюдается
условие dx1э/dω > 0 и полюсы, и нули
чередуются. Штриховыми линиями показаны
частотные характеристики при r2
≠ 0. Таким образом, резонансная кривая
I1 = F1(ω) цепи,
состоящей из двух связанных контуров
с малым затуханием, имеет два максимума
и один минимум.
а
рис. 6.24 представлена частотная
характеристика I1(ω)
при U1 = const, а также частотная
характеристика х1э(ω). Полюсами
функции х1э(ω) являются частоты
ω=0, ω=ω0 и ω=∞. Ее нулями являются
частоты ω=
и ω=
.
Во всем диапазоне частот соблюдается
условие dx1э/dω > 0 и полюсы, и нули
чередуются. Штриховыми линиями показаны
частотные характеристики при r2
≠ 0. Таким образом, резонансная кривая
I1 = F1(ω) цепи,
состоящей из двух связанных контуров
с малым затуханием, имеет два максимума
и один минимум.
