9.Разностные уравнения 1-го порядка. Пример формирования разностного уравнения для цепи, находящейся под воздействием последовательности прямоугольных импульсов.

Разностные уравнения:

Разностное уравнение описывает процессы при действии непрерывных сигналов – аналог дифференциального уравнения, которое описывает процессы при действии непрерывных сигналов.

Разностное уравнение связывает значения решётчатой функции в отдельные моменты времени.

Разностное уравнение 1-го порядка устанавливает связь между значением выходного сигнала в начале 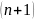-го интервала со значением в начале n-го интервала.

Формирование разностного уравнения 1-го порядка:

Пусть на вход цепи действует последовательность прямоугольных импульсов длительностью .

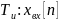Значение 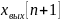можно получить методом наложения двух процессов:

1-й определяется энергией, накопленной к началу n-го интервала (к моменту nT).

2 -й процесс определяется только действием импульса, который пришёл в момент nT.

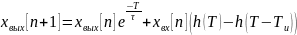
Общий вид разностного уравнения 1-го порядка:

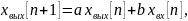
где 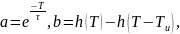h – переходная характеристика цепи.

Аналитическое решение разностного уравнения можно получить способом, схожим с классическим методом расчёта переходных процессов:

где 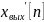– частное решение неоднородного разностного уравнения вида

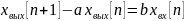
и – общее решение однородного разностного уравнения вида (штрихи не производные!):

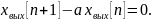
Пример:

Расчёт rL-цепи, находящейся под воздействием прямоугольных импульсов с амплитудой 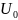и длительностью .

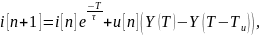
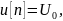
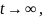
Частное решение найдём при 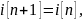подставляя в неоднородное уравнение, находим :

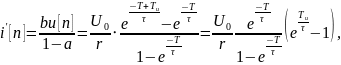
где

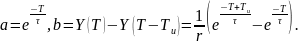
Однородное уравнение:

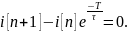
Характеристическое уравнение: .

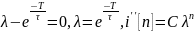С определим из начальных условий .

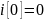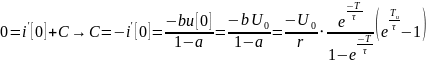
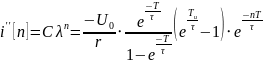
Решение:

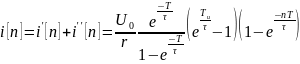
10. Формирование разностного уравнения для цепи 1-го порядка, находящейся под воздействием последовательности δ- импульсов.

Формирование разностного уравнения 1-го порядка при воздействии на входе цепи последовательности –импульсов площадью 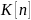(на примере rL – цепи).

Состояние цепи перед приходом очередного –импульса и сразу после –импульса отличаются, хотя и относятся к одному и тому же моменту nT. Обозначим значение тока до прихода импульса в момент nT, значение тока после прихода импульса в момент nT.

Перед приходом следующего –импульса в момент 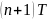ток падает по экспоненте:

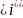
После прихода –импульса в момент

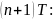
Получены два разностных уравнения:

В уравнении (*) дискретный момент времени nT – момент, предшествующий приходу импульса, а в уравнении (**) дискретный момент времени nT – момент, следующий за приходом импульса.

Для примера используем уравнение (**):

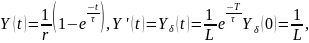
Аналитическое решение разностного уравнения можно получить как:

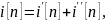
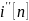где – частное решение неоднородного разностного уравнения, – общее решение однородного разностного уравнения.

Пусть .

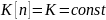При 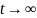подставляя в уравнение, находим :

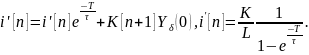
Однородное уравнение .

Характеристическое уравнение:

С определим из начальных условий:

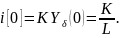
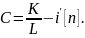
Решение:

11. z- преобразование. Примеры z-изображений решетчатых функций.

Вопросы 11-13 выглядят не так хорошо, как предыдущие, потому что в этих вопросах какое-то запредельное количество формул, идущих одна за другой. Поэтому было принято волевое решение вставить тупо скрины из учебника, потому что каждый из нас заколебался бы это расписывать словами, а поиск по словам в том тексте, который вставлен скринами, не особо нужен. И если вы поняли предыдущие вопросы, то с этими тремя тоже не должно возникнуть проблем.

Метод расчёта реакции цепи при действии последовательности импульсов, основанный на использовании z-преобразования, во многом аналогичен операторному методу. Он позволяет выполнить переход от последовательностей импульсов к их изображениям, преобразовать разностные соотношения между токами и напряжениями на элементах цепи к алгебраическим уравнениям, решить задачу для z-изображений и затем найти оригинал в виде последовательности импульсов искомой переменной.

Аналогия:

Операторный метод – для непрерывных функций времени,

Метод z-преобразования – для решетчатых функций.

Схема метода:

1. Переход от решетчатой функции 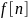к её z-изображению .

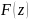2. Решение задачи для z-изображений.

3. Переход к оригиналу: искомой решетчатой функции.

Преобразование, определяющее соответствие решетчатой функции и её z-изображения , можно найти, вычисляя операторное изображение функци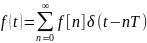и , которая описывает последовательность δ-импульсов интенсивностью (площадью) . Учитывая, что операторное изображение импульсной функции 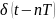равно 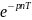, получаем 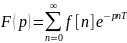. Обозначив , приходим к одностороннему прямому z-преобразованию решетчатой функции :

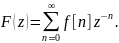
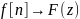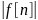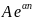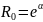Функцию называют z-изображением решетчатой функции , что условно можно записать в виде . Ряд сходится, если возрастает не быстрее, чем экспонента для всех z, лежащих вне окружности радиусом на комплексной плоскости. Дискретные последовательности импульсов токов и напряжений в электрических цепях удовлетворяют этим условиям.