5. Круговые диаграммы полных сопротивлений. Методика построения. Основные уравнения. [л3 2.1-2.5]

Круговая диаграмма полных сопротивлений – это графическое представление, которое помогает визуализировать различные компоненты сопротивления в электрической цепи. Эта диаграмма позволяет анализировать и понимать вклад каждого элемента в общее сопротивление цепи.

Шины посередине – точка m, при условии, что между генератором и системой линии нет.

Нужно построить годографы изменения вектора сопротивления (на реле сопротивления, установленном на шинах) при разных значениях q и δ. Точка N – номинальный режим.

ф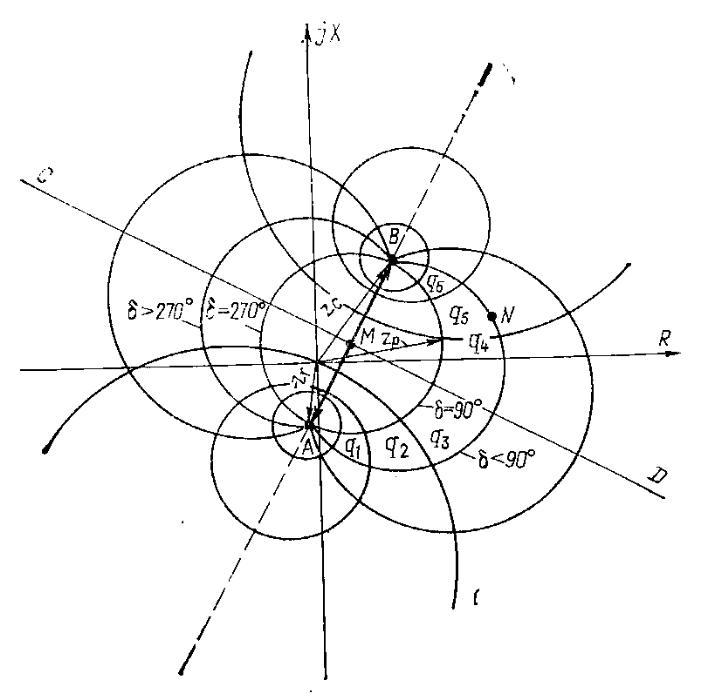

Годограф 1

Из-за того, что комплексные сопротивления генератора и системы имеют разные cos, сопротивления направлены не противоположно друг другу, из-за этого отрезок АВ не проходит через начало координат. Из-за того, что сопротивления генератора и системы не равны, прямая CD (годограф сопротивления при q=1) не проходит через начало координат.

Более идеализированный вариант представлен ниже, где допустим, что остальная энергосистема большая и устойчива. Тогда модуль ЭДС системы не меняется. И q изменяется за счёт изменения ЭДС генератора (тоже условно, ведь мы не можем сделать ЭДС генератора = бесконечность):

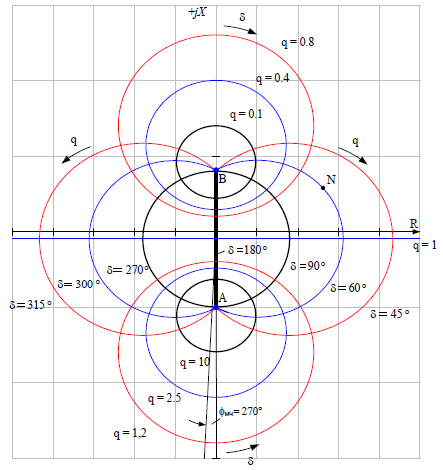
Годограф 2

2-5. Диаграммы полных сопротивлений на зажимах реле при изменении э. д. с. по концам электропередачи (Л3)

Полное сопротивление на зажимах реле определяется схемой включения обмоток напряжения и тока (гл. 5 и 6), параметрами и режимом работы системы.

При симметричном режиме работы системы отношение любых напряжений и токов может быть заменено отношением фазного напряжения к току одноименной фазы, с соответствующим множителем р:

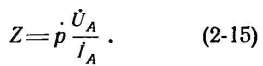
Значения множителя р для разных схем включения реле приведены в табл. 2-2, где k — коэффициент компенсации (см. $ 6-5).

Таблица 2-2.

При несимметричном режиме работы системы выражение сопротивления на зажимах реле получается более сложным.

Полное сопротивление на зажимах реле в общем случае (Л. 2-15—2-17)

Если расчетная схема представляет линейную электрическую систему (фиг. 2-6), то напряжение и ток, подводимые к зажимам реле на отправном конце, являются линейными функциями э. д. с. эквивалентных источников:

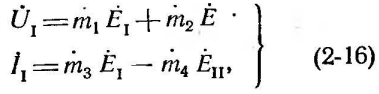
где - в общем случае комплексные коэффициенты, зависящие от параметров системы и схемы включения реле ( - безразмерные, - имеющие размерность проводимости).

В связи с этим выражение полного сопротивления на зажимах реле представляет дробнолинейную функцию вида:

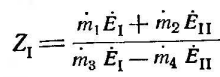
Значение , может быть выражено через отношения [Л. 2-15 и 2-16]:

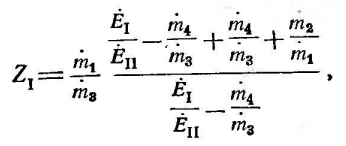откуда

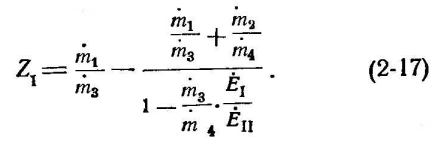
Аналогичным образом находим:

или, что то же

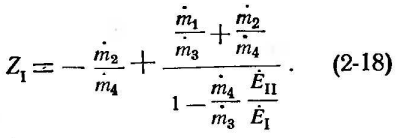
Обозначим:

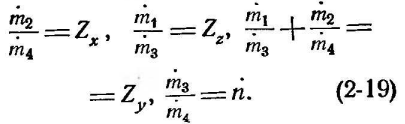При этом, выражения (2-17) и (2-18) перепишутся следующим образом:

и

Где - полные сопротивления; n - комплексное число.

В отдельных случаях может быть равно нулю, а коэффициент n может быть равен единице.

Положим, что комплексные величины, входящие в (2-20) и (2-21), имеют

следующие модули и аргументы:

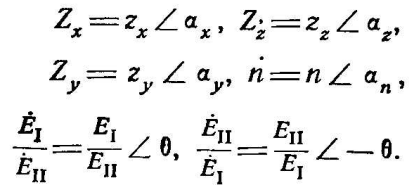При этом, выражения 20 и 21 принимают следующий вид:

и

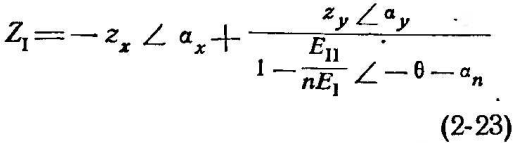
Величины , n могут быть получены различными способами [Л. 2-15-2-17].

Один из способов [Л. 2-15] сводится к тому, что симметричные составляющие токов и напряжений, подводимых к реле, выражаются через сопротивления элементов системы на основании расчетной схемы, соответствующей исследуемому режиму работы электропередачи.

При помощи симметричных составляющих для заданного сочетания токов и напряжений на зажимах реле записывается выражение (2-16), из которого выявляются коэффициенты . Искомые величины , n определяются в этом случае на основании (2-19). Второй способ [Л. 2-16 и 2-17] заключается в том, что сопротивления , находятся поочередно в предположении, что . При Е₁=0 согласно (2-21)

(2-24)

При Е_II=0 согласно (2-20)

(2-25), тогда

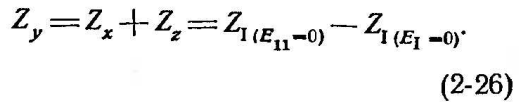Положив далее получаем на основании 20 и 21:

откуда, с учетом 24 и 26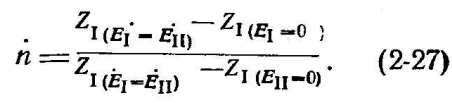

При отсутствии повреждения и учете в расчетной схеме только продольных сопротивлений (если ветви проводимостей не учитываются), сопротивление

обращается в бесконечность и соответственно коэффициент n равен единице.

При этом, как это следует из (2-24)-(2-26), величина определяется сопротивлением конца электропередачи до места установки реле (включая сопротивление эквивалентного источника); величина , определяется сопротивлением остальной части электропередачи, а ,- сопротивлением всей электропередачи, включая сопротивления обоих источников (т. е. отношением ).

Определив , n, можно на основании (2-22) или (2-23) построить геометрические места конца вектора 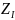, в зависимости от значения угла (и постоянных значениях ) и в зависимости от отношения (при постоянных значениях угла). При этом в соответствии с $2-2 и 2-3 на комплексной плоскости сопротивлений получаются два семейства круговых диаграмм.

На фиг. 2-7 изображены круговые диаграммы полных сопротивлений при заданных величинах , n, [Л.2-16].

Сопротивление на зажимах реле определяется вектором, начало которого совпадает с началом координат, а конец располагается на соответствующей окружности.

При ЕI =0 получается вектор , с концом в точке А,

а при ЕII=0 - вектор , с концом в точке В. Вектор АВ изображает .

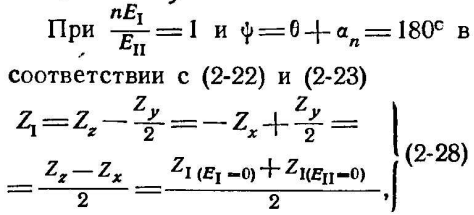
т. е. середина линии АВ совпадает с концом вектора , изображаемого на фиг. 2-7 отрезком ОМ.

а) При постоянном значении изменении угла , от 0 до 360°, конец вектора , в соответствии с (2-22) или (2-23) описывает окружность, положение центра и. величина радиуса которой находятся на основании указаний $ 2-3.

Из сопоставления (2-22) с (2-5) следует, что в данном случае . Поэтому согласно (2-10) радиус окружности

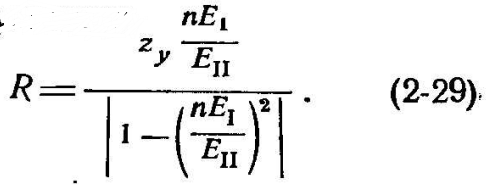
Центр круговой диаграммы совпадает с концом вектора

Уравнение (2-30) является уравнением линии центров семейства окружностей, соответствующих постоянным значениям Выше было показано, что величина

входящая в (2-30), представляется на комплексной плоскости вектором ОМ, конец которого совпадает с серединой отрезка АВ. Второе же слагаемое в правой части (2-30) означает вектор МС, совпадающий по направлению

с вектором МВ — при, или с вектором МА— при

В первом случае ( )круговые диаграммы пересекают линию АВ в точках, расположенных в направлении МВ; во втором случае круговые диаграммы пересекают линию АВ в точках, расположенных в направлении МА. На фиг. 2-7 это показано для значений , равных соответственно 1,5 и 0,75.

Аналогично предыдущему, сопоставляя (2-23) с (2-5), можно получить радиус окружности

Наконец, если положить , то на основании (2-29) и (2-31) и радиус окружности обратится в бесконечность. Круговая диаграмма превратится в данном случае в прямую, перпендикулярную отрезку АВ в средней его точке (линия GН на фиг. 2-7).

б) При постоянном значении угла и изменении отношения , конец вектора , описывает окружность, положение центра и величина радиуса которой находятся на основании указаний параграфа 2-2.

С учетом (2-8) радиус окружности определяется из выражения

При радиус обращается в бесконечность.

В $2-2 было показано, что независимо от значения угла ф окружности, описываемые концом вектора N (2-5), пересекают ось действительных величин в точках 0 и 1. С учетом выражения (2-20) точки, в которых пересекается семейство окружностей, определяются концами векторов ., (точка В) и (точка А).

Центр окружности при заданном значении угла в соответствии с $2-2 совпадает с концом вектора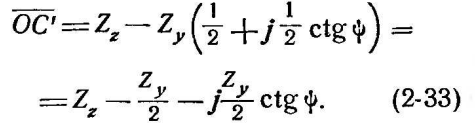

Величина , определяется вектором ОМ, конец которого совпадает с серединой отрезка АВ, а второе слагаемое (2-33) представляет вектор, перпендикулярный отрезку АВ: Таким образом, линия центров окружностей при постоянных значениях Ψ делит линию АВ пополам и перпендикулярна к ней; уравнением ее служит уравнение (2-33).

При положительных значениях ctg Ψ центр С’ располагается в направлении МН; при отрицательных же значениях ctg Ψ центр располагается в сторону МG.

Наконец, при ctgΨ=0, что соответствует Ψ = 90° и Ψ =270°, центр окружности находится в точке пересечения линий АВ и GН.

Симметричный режим работы электропередачи.

Рассмотрим методику построения диаграмм полных сопротивлений применительно к расчетной схеме с четырехполюсником при расхождении э.д.с. по фазе, не сопровождаемом коротким замыканием. В этом случае расчетная схема, изображенная на фиг. 2-6, представляет схему прямой последовательности.

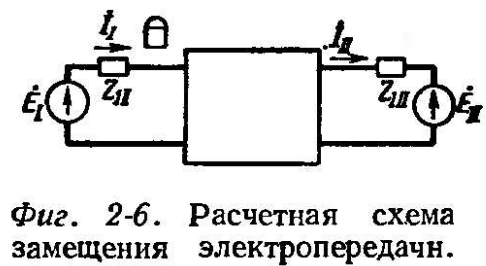
Сопротивление на зажимах реле, установленного в какой-либо точке, например на отправном конце электропередачи, определяется выражением (2-15).

Положим, что множитель р, входящий в (2-15), равен единице.

Для нахождения выражения (2-15) воспользуемся соотношением

откуда

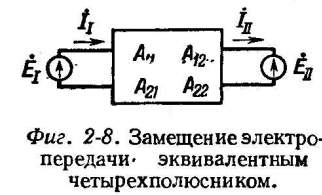
Схема 2-6, содержащая четырехполюсник с последовательно включенными по концам сопротивлениями источников, может быть замещена эквивалентным четырехполюсником, имеющим согласно табл. 2-1 параметры А11, А12, А21, А22 (фиг. 2-8). При этом

На основании (2-35) и (2-36) ток в начале электропередачи равен:

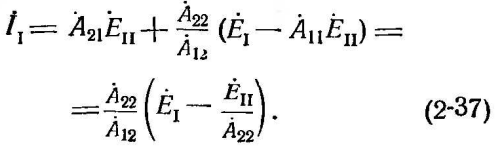
Подстановка (2-37) в (2-34) дает:

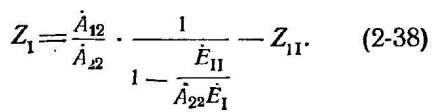
Полученное выражение соответствует уравнению (2-21). Отношение

представляет собой входное сопротивление четырехполюсника (фиг. 2-8), измеренное со стороны источника э. д. с. ЕI, при закороченных выходных зажимах (ЕII = 0). Когда проводимости не учитываются, то А22=1, А12=Z, т.е. равно сопротивлению Z всей электропередачи.

Фиг. 2-9 Замещение электропередачи эквивалентным четырехполюсником с измененными положительными направлениями токов

При построении характеристик реле у приемного конца электропередачи положительное направление тока может быть принято таким же, как и на от правном конце, — от шин в сторону линии. В этом случае (фиг. 2-9)

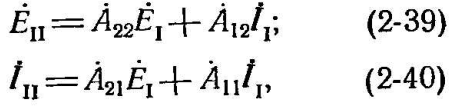откуда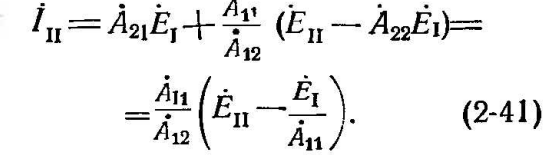

В связи с этим сопротивление на зажимах реле

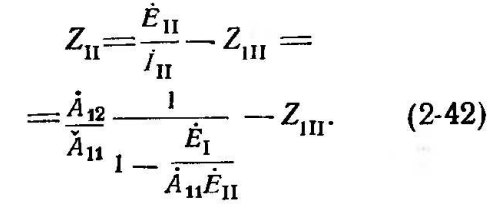
Построение на основании (2-38) диаграмм полных сопротивлений значительно облегчается при условии, когда модуль

В этом случае выражение 38 преобразуется следующим образом:

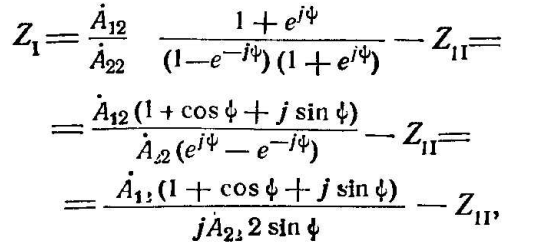
где аргумент комплексного параметра А22. Отсюда

Сравнивая (2-44) с (2-33), убеждаемся в том, что полученное геометрическое место представляет прямую, совпадающую с линией центров окружностей. На основании (2-44) может быть построен график , для различных соотношений и для различных значений угла. Если положить, что углы полных сопротивлений и одинаковы и равны , то график примет вид фиг. 2-10.

Фиг. 2-10. Геометрическое место конца вектора полного сопротивления при симметричном режиме электропередачи (без короткого замыкания).

В этом случае, как это следует из (2-44), геометрическим местом конца вектора , при изменении отношения от нуля до единицы (при постоянных значениях угла Ψ) служит семейство прямых, образующих с осью действительных величин угол . В свою очередь, при изменении угла Ψ и постоянных значениях отношения геометрическим местом конца вектора , является семейство прямых, перпендикулярных к первому семейству. Как видно из фиг. 2-10, масштаб углов Ψ неравномерен: при изменении угла Ψ по мере приближения конца вектора , к началу координат масштаб углов уменьшается.

При значении угла Ψ, равном нулю и соблюдении условия (2-43) ток I1 на

отправном конце электропередачи в соответствии с (2-37) равен нулю, и поэтому сопротивление согласно (2-44) обращается в бесконечность.

Если множитель р, входящий в исходное выражение (2-15), отличен оn единицы (см. табл. 2-2), то диаграмма (фиг. 2-10) должна быть изменена в линейных размерах в р раз и повернута на соответствующий угол, указанный в табл. 2-2.

В общем случае работы электропередачи условие (2-43) может не соблюдаться. При этом геометрическим местом конца вектора определяемого формулой (2-38), будут служить два семейства окружностей, отвечающих функциональным зависимостям (при постоянных значениях угла Ψ) и от угла Ψ(при постоянных значениях ).

Выше была пояснена общая методика построения круговых диаграмм, иллюстрированная в виде примера на фиг. 2-7.

6 вопрос: Направление протекания токов симметричных составляющих по концам ЛЭП при К3, К1, К1,1, К2, обрыве, К1+обрыв. Продемонстрировать на векторных диаграммах. [Л2 1.6; Л10 гл.11, Л9 15.8, 17.1-4]

Федосеев 1992 год (п 1-6)

• Переходные сопротивления в месте повреждения:

Таблица 1. Виды повреждений

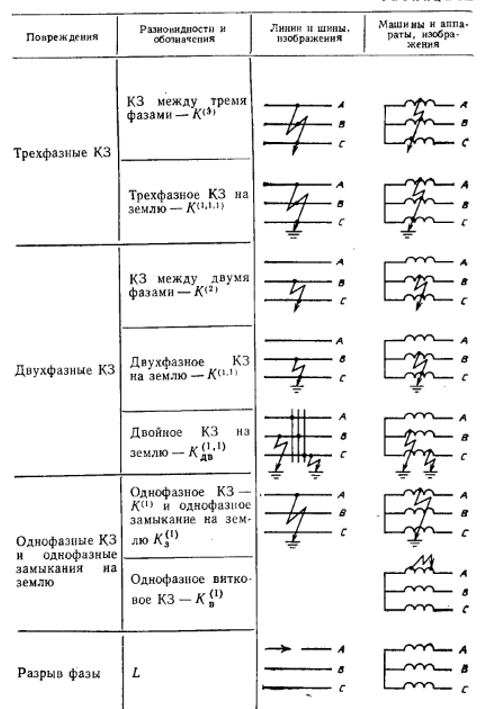
Переходные сопротивления в общем случае определяются сопротивлениями электрических дуг, посторонних предметов в месте повреждения, опор и их заземлений, а также сопротивлениями между проводами фаз и землей.

• Короткие замыкания в одной точке:

КЗ в одной точке К трёхфазной системы через переходные сопротивления неодинаковых значений может быть представлено схемой на рисунке 1.

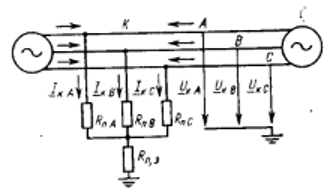
Рис. 1. Общий случай КЗ в одной точке через переходные сопротивления

Здесь и в дальнейшем за условные положительные направления токов КЗ принимаются направления токов в фазах линии к месту повреждения, в ответвлении КЗ – от фаз к земле, а фазных напряжений – также от фаз к земле.

Возникшее КЗ характеризуется уравнениями:

;

;

.

Фазные напряжения в точке КЗ и токи , проходящие через , могут быть выражены через симметричные составляющие.

При малых или равных нулю , КЗ называются – металлическими.

На практике обычно пользуются более упрощенными выражениями, в которых принимаются равными нулю, бесконечности или равными между собой (рисунок 2).

Рис. 2. Примеры упрощённого учета в месте КЗ.

• Расчётные условия:

Работа защитных устройств при КЗ определяется периодическими слагающими промышленной частоты токов и напряжений , подводимых к реле, а также сдвигами по фазе между ними. В целях упрощения рассматриваются характеризующие их соотношения для ненагруженной линии с односторонним питанием в начальный момент повреждения.

Рис. 3. Повреждение на ненагруженной линии с односторонним питанием.

• Трёхфазные КЗ в одной точке:

Векторная диаграмма напряжений и токов фаз при в точке К линии (на расстоянии, характеризуемом приведены на рисунке 4.

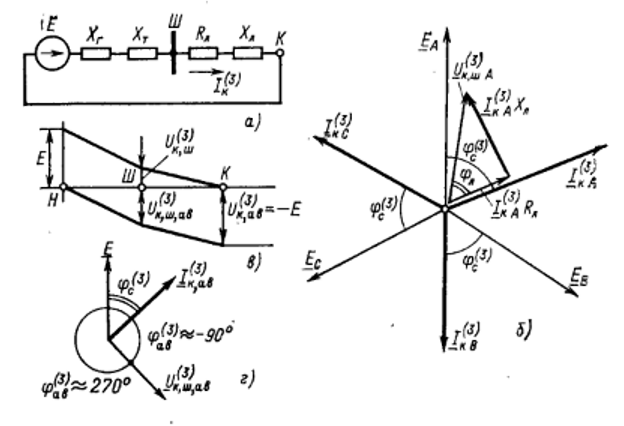Рис. 4. Соотношения электрических величин при металлическом .

Рис. 5. Схема соединения при трёхфазном КЗ.

Токи при принятых условных положительных направлениях отстают от соответствующих ЭДС на угол . Остаточные фазные и междуфазные напряжения возрастают по мере удаления от места КЗ, где . Например, напряжение на шинах . Фазные напряжения опережают соответствующие им токи на угол .

При КЗ через симметричные : ; ; . ВД остается той же, только поворачивается на угол, определяемый группой соединения трансформатора, до совпадения Е по фазе с (на .

Аварийные слагаемые: токи остаются теми же . Для напряжения в месте КЗ (рис. 4, в). При металлическом КЗ, когда , . Аварийные напряжения уменьшаются по мере удаления от места повреждения. Они имеют наибольшее значение в точке К и равны нулю в нейтралях генераторов.

• Двухфазные КЗ в одной точке:

Рассматриваются , в системе с изолированными нейтралями и в системе с глухозаземлёнными нейтралями.

Векторная диаграмма полных напряжений и токов фаз при в точке К линии приведены на рисунке 5.

Рис. 6. Соотношения электрических величин при .

Рис. 7. Схема соединения при двухфазном КЗ в одной точке.

Граничные условия для : в неповреждённой фазе А отсутствует, , . Токи определяются ЭДС , действующей в контуре их циркуляции. При принятом равенстве сопротивлений прямой и обратной последовательностей ток отстаёт от на угол . Фазное напряжение , фазные напряжения , поскольку сумма во всех точках системы, в том числе и в точке К, остаётся равной нулю.

Напряжения в нейтралях генератора и трансформатора (если бы даже нейтраль последнего была не заземлена), как и при нормальной работе, равны нулю. По мере удаления от места повреждения остаётся неизменным, напряжения повреждённых фаз изменяются. Например, на шинах Ш:

;

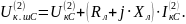
Напряжение . Оно опережает ток на угол (как при ).

Следует ответить, что фазные напряжения и с учетом того, что , оказываются неравными, причём напряжение опережающей фазы В больше, чем отстающей фазы С.

Еще большие искажения ВД напряжений возникают при повреждениях через . Учёт при повреждениях обусловливает изменения напряжений фаз по дугам окружностей. Учёт равных в фазах В и С осуществляется включением в месте повреждения сопротивления .

В случае, когда углы сопротивлений отдельных элементов системы до точки К равны , получаются простые ВД напряжений. В этом случае концы векторов напряжений фаз В и С по мере удаления от места повреждения скользят по прямой, соединяющей концы векторов и 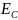, а напряжение совпадает по фазе с (рис. 5, б).

Напряжение прямой последовательности имеет наименьшее значение в месте повреждения и возрастает по направлению к источнику питания (рис. 5, в). Напряжение обратной последовательности наоборот, максимально в точке повреждения и снижается в том же направлении. Угол сдвига при , как и при других видах несимметричных КЗ, не зависит от , поскольку определяется только сопротивлениями элементов системы, и близок к 270° (или -90°) (рис. 5, г).

Только при , как это принималось выше, напряжение неповреждённой фазы . Это сказывается и на напряжениях повреждённых фаз; например, для точки Ш , а не .

• Двухфазное КЗ на землю в сети с изолированными нейтралями:

Двухфазные КЗ на землю в сетях с изолированными нейтралями или заземлёнными через дугогасящие реакторы (в России это сети с ) отличаются от в основном только тем, что повреждённые фазы, например В и С, в месте металлического КЗ принуждённо приобретают потенциал земли; появляется напряжение нулевой последовательности практически одинаковое во всей сети. Нейтраль системы (трансформатора) получает по отношению к земле смещение , а напряжение неповреждённой фазы А возрастает до . Значения токов повреждённых фаз, междуфазных напряжений и их фазные соотношения остаются такими же, как при . За трансформатором, в системе генераторного напряжения смещения нейтрали генератора не происходит, так как трансформируются только составляющие прямой и обратной последовательностей.

• Двухфазное КЗ на землю в сети с глухозаземленными нейтралями:

Двухфазные КЗ на землю в сетях с глухозаземлёнными нейтралями (рис. 3) могут сопровождаться сильным снижением как междуфазного, так и фазных напряжений повреждённых фаз (в месте КЗ до нуля пр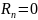и и ) и появлением составляющих нулевой последовательности не только в фазных напряжениях (как в сетях с изолированными нейтралями), но и в токах. Соотношения электрических величин при этом виде повреждений наиболее просто выявляются при использовании метода симметричных составляющих.

Примерный вид ВД полных токов и напряжений на рис. 6. Угол δ между токами и повреждённых фаз в общем случае изменяется в широких пределах: , причем верхний предел относится к случаю обычного , когда , а нижний (нереальный) соответствует . Ток, проходящий через в землю .

Переходное сопротивление на землю в приведенные выражения для не входит и угол .

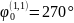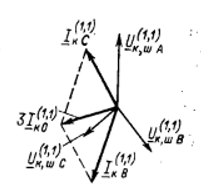
Рис. 8. Соотношения электрических величин при .

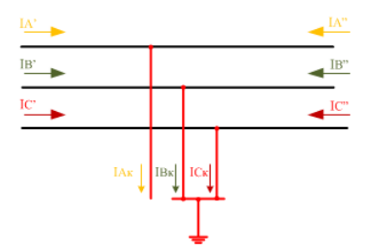
Рис. 9. Схема соединения при двухфазном КЗ на землю.

Из всех видов несимметричных двухфазных КЗ рассматриваемые характеризуются наименьшими значениями напряжений прямой последовательности и поэтому являются наиболее тяжелыми (расчётными) по условиям сохранения устойчивой работы системы.

• Однофазные КЗ в сети с глухозаземлёнными нейтралями:

Комплексная схема последовательностей на рис. 7, при учёте, что особой является фаза А, имеющая в точке К переходное сопротивление на землю, приведена на рис. 7, а.

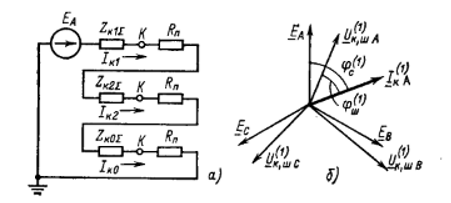
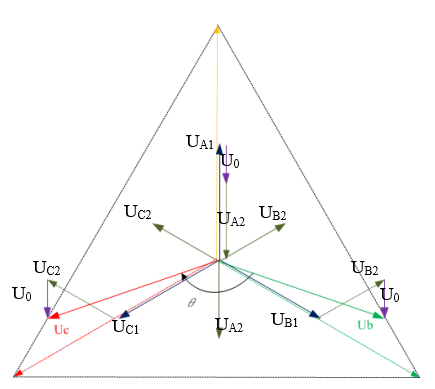
Рис. 10. Соотношения электрических величин при через .

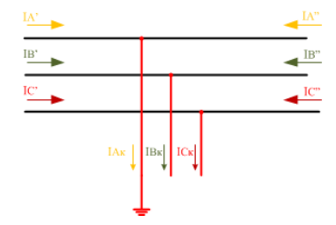
Рис. 11. Схема соединения при однофазном КЗ.

Граничные условия: , , .

Токи при однофазном КЗ:

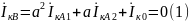
Вычтем из уравнения (1) уравнение (2):

Подставим (3) в уравнение (1):

Симметричные составляющие:

Напряжения при однофазном КЗ:

Симметричные составляющие напряжений в месте КЗ:

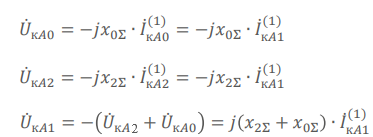
Граничные условия характеризуются соотношениям , , . В соответствие со схемой и . Соотношения между напряжениями и токами нулевой и обратной последовательностей определяется, как для . На угол не влияет, и он примерно равен 270°.

На ВД (рис. 7, б) отстаёт от на угол .

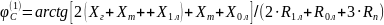Фазное напряжение при приближении к источнику питания возрастает, и в месте Ш установки защиты . Угол между и в месте КЗ , а у шин .

При равенстве сопротивлений во всех трёх последовательностях напряжения неповреждённых фаз В и С остаются равными и с углом сдвига 120°. Примерный вид этих напряжений показан на ВД с условием, что сопротивление нулевой последовательности больше, чем прямой последовательности.

При определении токов КЗ часто учитываются только реактивные сопротивления элементов системы, а принимаются равными нулю. В этом случае токи и в месте КЗ:

.

Отношение токов нулевой последовательности в месте повреждения при и :

• при :

.

• при

.

• при

.

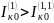Эти соотношения для КЗ на одиночных линиях справедливы и для всех ветвей схем нулевой последовательности, поскольку коэффициенты токораспределения в схеме нулевой последовательности не зависят от вида повреждения.

В общем случае при по неповреждённым фазам, даже при отсутствии токов нагрузки, проходят токи КЗ. В пределе они достигают значения тока КЗ в повреждённой фазе. В Этом случае ток , проходящий через заземлённую нейтраль понижающего трансформатора Т2 (рис. 8), принужденно (поскольку токи в его обмотках, соединенных в треугольник, должны быть равны) распределяется между тремя фазами линии на три равные составляющие , являющиеся полными токами фаз с этой ее стороны. За местом повреждения К, в сторону повышающего трансформатора Т1 с изолированной нейтралью, токи в неповреждённых фазах остаются такими же, как и со стороны Т2. Однако они уже не являются токами нулевой последовательности, а содержат составляющие только прямой и обратной последовательностей, так как со стороны Т1 .

Рис. 8. Предельный случай распределения токов при .

Однофазные КЗ представляют собой тяжёлый вид повреждения, хотя и менее опасный для системы, чем многофазные. Они должны отключаться также по возможности быстро. Защита может действовать на отключение всех трёх фаз линии или только одной повреждённой с последующим ее автоматическим повторным включением. Последний способ целесообразен для магистральной линии (преимущественно одноцепных) при наличии у выключателей пофазного привода и в некоторых других случаях. Часто самоликвидируются. В сетях 300-500 кВ применяется почти всегда, а в 110- 220 кВ реже.

Для защит от часто используются составляющие нулевой последовательности, так как при этом обеспечиваются независимость от рабочих токов и напряжений и некоторые другие преимущества.

• Двойные КЗ на землю:

Двойные замыкания на землю учитываются только в сетях с нейтралями, изолированными или заземленными через дугогасящие реакторы. (сети с 35 кВ или ниже).

Предполагается (рис. 8, а), что фаза В замкнулась на землю в точке , а фаза С – в точке сети. По поврежденным фазам проходят токи . В неповрежденной фазе А ток отсутствует.

Если точки и лежат на разных линиях (рис. 8, 6), токи КЗ существуют только в одной поврежденной фазе каждой линии. Ток в земле между точками и следует при этом считать проходящим, как показано пунктиром, по трассе: точка – шины подстанции – точка .

В общем случае при двустороннем питании токи КЗ могут появляться и в неповреждённой фазе, достигая в пределе значений токов в поврежденных фазах. Предполагается, что линия питается от систем бесконечной мощности ( ) с одинаковыми э. д. с. (рис. 8, в). Токи поврежденной линии определяются из соотношений для трех контуров между местами пробоя, расположенными по краям линии, в каждый из которых входит одна из фаз:

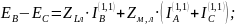
откуда

,

где и – соответственно сопротивления провод-земля и сопротивление взаимоиндукции между проводами.

Таким образом, во всех трёх фазах линии токи равны, т.е. являются токами нулевой последовательности.

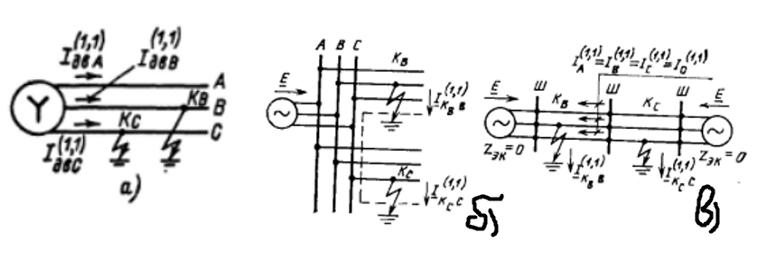
Рис. 9. Двойное замыкание на землю в сети с изолированной нейтралью.

а – схема сети с односторонним питанием; б – путь прохождения тока через землю (пунктир); в – схема сети с двусторонним питанием.

Таким образом, в рассматриваемом предельном случае токи во всех трёх фазах равны, т.е. имеют только составляющие нулевой последовательности. В реальных случаях необходимо считаться с наличием тока в неповреждённой фазе, за исключением случаев, подобных данному, где он равен нулю.

Этот вид КЗ сложный, так как характеризуется возникновением несимметрии (поперечной) в двух местах электрической сети.

Напряжения между повреждёнными фазами в отличие от фазных во всех точках сети, в том числе и в местах повреждения, имеют конечные значения, уменьшаются при сближении этих мест и при их совпадении равны нулю, а повреждение превращается в в одной точке. Сдвиг по фазе имеет сильно изменяющиеся значения, отличающиеся от в связи с влиянием переходных сопротивлений на землю.

В случае на разных участках сети обычно представляется более целесообразным автоматически отключать только одно место пробоя.

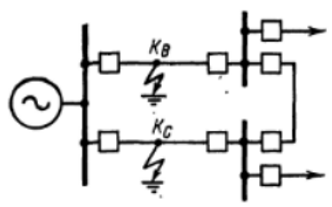
Рис. 10. Двойное замыкание на землю, которое может привести к полному отключению сети.

Обеспечение отключения по возможности одного места пробоя осуществляется посредством двухфазного (а не трехфазного) выполнения защит.

При продольной несимметрии, в отличие от поперечной, как ЭДС, так и сопротивления, отнесённые к точке несимметрии, складываются соответственно последовательно, а не параллельно.

• Разрыв одной фазы – обрыв:

Характеризуется следующими граничными условиями: и .

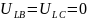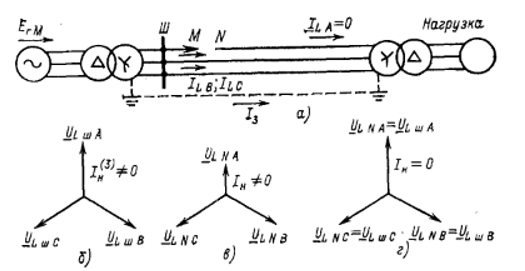
Рис. 11. Соотношения электрических величин при разрыве одной фазы на линии, питающей нагрузку

На рисунке 11 (а) представлен частный случай разрыва фазы А на выключателе линии, питающей нагрузку. На рисунке 11 (б-г) показаны возможные ВД напряжений, характеризующие рассматриваемый разрыв. Напряжение фазы А на шинах источника питания сохраняет значение, близкое к рабочему напряжению предшествующего разрыву режима рисунок 11 (б). Напряжение той же фазы А за разрывом , рисунок 11 (в), будет отличаться от на величину , пропорциональную току нагрузки в рабочем режиме ( ), и иметь конечное значение. Это определяется наведением в фазе А ЭДС, соответствующей напряжению в обмотке низшего напряжения понижающего трансформатора, соединенной в треугольник. При холостой работе линии и рисунок 11 (г). Таким образом, напряжения фазы А с обеих сторон разрыва оказываются одинаковыми. Напряжения фаз В и С с обеих сторон места разрыва, изменяясь по сравнению с в зависимости от значения , во всех режимах одинаковы: и , рисунок 11 (б-г).

При принятом положительном направлении тока в земле , совпадающем с направлениями токов и , . Сумма (ток 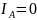, однако имеет составляющие, в том числе , не равные нулю). Наличие определяет угол между , меньший 120°.

• Однофазное КЗ на одной из фаз и разрыве двух других фаз:

При однофазном КЗ на фазе А и разрыве двух других фаз В и С, фаза с является особой.

Полные токи КЗ со стороны обеих систем и , направленные к месту повреждения К, при отсутствии переходного сопротивления в месте повреждения замыкаются по независимым контурам, рисунок 12. Поэтому они рассчитываются как токи однофазного КЗ на линии с односторонним питанием по выражению , где и сопротивления Z определяются данными соответственно систем M и N и сопротивлениями повреждённой линии по обе стороны от точки КЗ. Ток в месте КЗ равен их сумме.

Рис. 12. КЗ на одной фазе и разрыв двух других.

Вагнер (глава 11)

НАПРЯЖЕНИЯ И ТОКИ СИЛОВЫХ СИСТЕМ В УСЛОВИЯХ КЗ

• Основные допущения:

Система симметрична полностью за исключением одного только места короткого замыкания.

Рассматриваем следующие виды КЗ:

1. Трёхполюсное (трёхфазное) (3Ф – 3);

2. Однополюсное (однофазное) (Ф – 3);

3. Двухполюсное на землю (двухфазное на землю) (2Ф – 3);

4. Двухполюсное (двухфазное) (Ф – Ф).

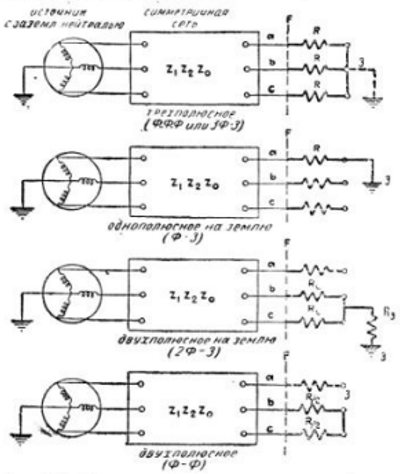
Рис. 111. Виды КЗ в трёхфазных системах.

В дальнейшем будет допущено, что все генерируемые эдс могут быть приведены к одному эквивалентному генератору с эдс* прямой последовательности 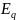и что эквивалентные цепи могут быть представлены последовательными сопротивлениями соответственно для схем прямой, обратной и нулевой последовательностей.

• Формулы для линейных токов и линейных и фазовых напряжений:

По методу симметричных составляющих:

Таблица 1. Токи короткого замыкания

Таблица 2. Напряжения в точке короткого замыкания

• Основания для сравнения систем

Решающими соображениями при составлении кривых для несимметричных условий было нахождение параметров, удобных для сравнения всех возможных систем. Были взяты следующие величины:

- для фазовых (фазных) U – нормальное фазовое напряжение;

- для линейного напряжения – нормальное линейное напряжение;

- для токов – трехфазный ток КЗ;

- для сопротивлений – реактивное сопротивление прямой последовательности.

Все отношения даны не в вольтах, амперах и омах, а в виде отношений или десятичных долей исходных величин.

Все напряжения подсчитаны для точки F по рис. 111.

Рис. 112. Кривые зависимости токов КЗ от реактивных сопротивлений системы одно- и двухфазного КЗ на землю. Все токи выражены как отношения к току трехфазного КЗ. Активные сопротивления равны 0.

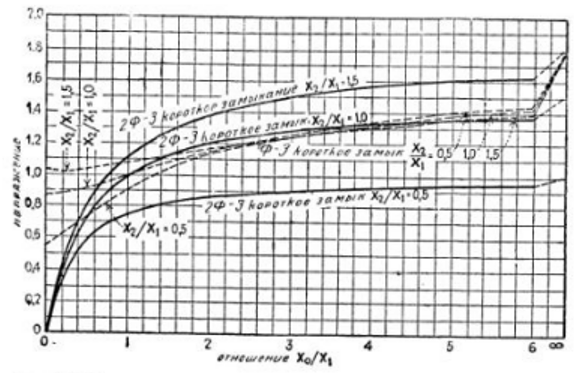
Рис. 113. Кривые зависимости напряжений КЗ от реактивных сопротивлений системы одно- и двухфазного КЗ на землю. Напряжения представлены как фазные и выражены как отношение к нормальному фазному напряжению. Активные сопротивления равны 0.

Ульянов (п. 15-8)

ВЕКТОРНЫЕ ДИАГРАММЫ ТОКОВ И НАПРЯЖЕНИЙ

КАК В 7 ВОПРОСЕ – ТАМ ТАКОЙ ЖЕ ИСТОЧНИК ЛИТЕРАТУРЫ И ТЕ ЖЕ СТРАНИЦЫ