4. Применение полного перебора для решения задачи о рюкзаке. Перебор всех подмножеств множества. Сведение к перебору двоичных векторов. Коды Грея.

Определение: Задача о рюкзаке: Дан рюкзак грузоподъёмности V и n предметов с указанной ценностью a_j > 0 и весом c_о > 0. Цель: Заполнить рюкзак, получив наибольшую ценность.

Вариант решения полным перебором с помощью алгоритма генерации кодов Грея:

Вариант решения поиска с возвратом с помощью рекурсий векторов 0-1:

5. Общая схема метода ветвей и границ. Применение метода ветвей и границ для решения задачи о рюкзаке

Определение: Задача о рюкзаке: Дан рюкзак грузоподъёмности V и n предметов с указанной ценностью a_j > 0 и весом c_о > 0. Цель: Заполнить рюкзак, получив наибольшую ценность.

Определение: Метод ветвей и границ (Branch and Bound) основан на комбинировании перебора и оценки наборов предметов, чтобы исключить неперспективные варианты и сократить поиск оптимального решения.

Определение: Ветвление - это функция β, которая каждому подмножеству A множества Ω ставит в соответствие некоторое его разбиение. Если |A| > 1, то β(A) = {A₁, A₂, ..., A_k } Если |A| ≤ 1, то β(A) = ∅.

О пределение: Оценка - это функция ψ : 2^Ω → R, для которой ψ(A) ≥ φ(x) для всех x ∈ A; ψ(A) = φ(x), если A = {x}. Величина ψ(A) оценивает сверху значения функции φ на множестве A и совпадает с ней на множествах, состоящих из одного элемента. Для вычисления оценки решается упрощенная оптимизационная задача.

При этом на каждом шаге обновляем рекорд при обнаружении лучшего решения.

Метод ветвей и границ относится к классу точных методов. Он позволяет сократить число рассматриваемых вариантов решений по сравнению с полным перебором, но в худшем случае сводится к нему.

6. Динамическое программирование

Определение: Динамическое программирование (Dynamic Programming) - это метод решения сложных задач, которые можно разбить на более простые подзадачи и затем комбинировать их оптимальным образом. Он использует идею сохранения промежуточных результатов для избегания повторных вычислений и повышения эффективности.

Определение: Задача линейного раскроя: Дан стержень длины L и n видов деталей. Деталь вида j имеет длину a_j > 0 и цену c_j > 0, j = 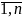. Цель: раскроить стержень на детали с максимальной стоимостью по итогу.

Временная сложность алгоритма: O(L*n)

Решение для задачи о рюкзаке:

Определение: Задача про перемножение матриц (выбор скобок): Дан набор матриц, требуется найти оптимальный порядок их перемножения с минимальным количеством умножений.

Код алгоритм:

for i = 1 to n do f_ii = 0 i = 1, j = 2, t = 2 while j – i < n do f_ij = ∞ for k = i to j – 1 do q = f_ik + f_k+1j + p_i-1p_kp_j if q < f_ij then f_ij = q, g_ij = k i++, j++ if j = n then i = 1, t++, j = t

Код перемножения матриц: Запуск: MULT(1, n) MULT(i, j) if j > i then X = MULT(i, g_ij) Y = MULT(g_ij+1, j) return XY else return Mi

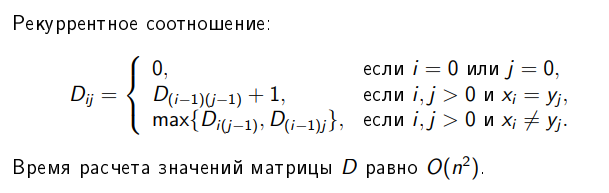4. Задача о наибольшей общей подпоследовательности (Longest Common Subsequence, LCS):

Формулировка: Даны две последовательности элементов, требуется найти подпоследовательность наибольшей длины.

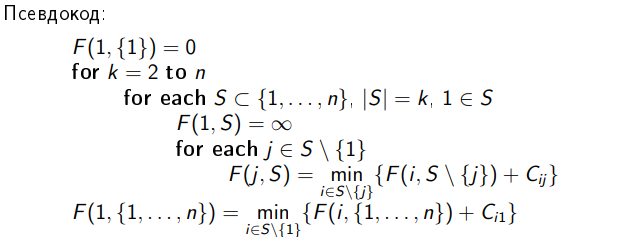5. Задача коммивояжера (Traveling Salesman Problem):

Даны города, нужно каждый из них обойти наикратчайшим путём единожды, вернувшись в конце к исходному.

Матмодель: Поиск гамильтонова цикла в графе, где вершины – города, а грани – дороги между ними.

Время: O(n²2ⁿ)

Свойства задач, для которых применимо динамическое программирование:

- Можно разбить на подзадачи, что оптимально скажется на вычислении решения. - Обладает перекрывающимися подзадачами, т.е. вычисление оптимального решения для одной подзадачи может потребоваться для вычисления оптимального решения других подзадач.

Сравнение с полным перебором: Динамическое программирование использует принцип оптимальной подструктуры и сохраняет результаты промежуточных вычислений, что позволяет избежать повторных вычислений и значительно ускоряет процесс. На что полный перебор не способен)