
Тройные интегралы 26-28
.doc
ТРОЙНЫЕ ИНТЕГРАЛЫ
26. ТРОЙНЫЕ ИНТЕГРАЛЫ И ИХ СВОЙСТВА
Теорема
о существовании тройного интеграла:
Если
подынтегральная функция
![]() непрерывна на области V,
то она интегрируема по этой области.
непрерывна на области V,
то она интегрируема по этой области.
] в некоторой замкнутой ограниченной области T трёхмерного пространства задана ограниченная функция трёх переменных f(x,y,z). Разобьём эту область на n произвольных частей с объёмами vi. В каждой частичной области возьмём произвольную точку M(xi,yi,zi) и составим сумму:
 ,
,
которая
называется интегральной
суммой
для функции f(x,y,z)
по области T.
Если
![]() и интегральная сумма при n
имеет предел, то такой предел называется
тройным
интегралом:
и интегральная сумма при n
имеет предел, то такой предел называется
тройным
интегралом:
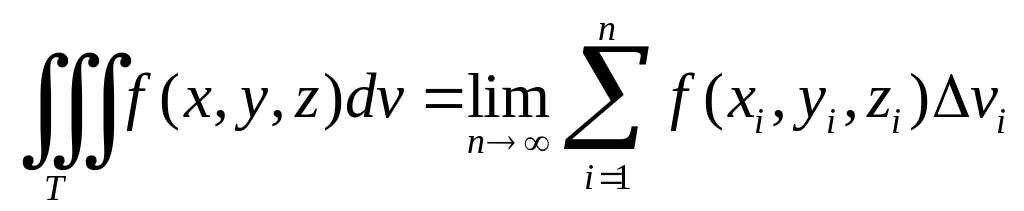 (2.1)
(2.1)
Свойства тройного интеграла: по смыслу и доказательству полностью аналогичны свойствам определённого и двойного интегралов.
1.
Линейность.
Если функции
,
![]() интегрируемы по области
V,
то их линейная комбинация
интегрируемы по области
V,
то их линейная комбинация
![]() тоже интегрируема по
тоже интегрируема по
![]() ,
и:
,
и: ![]()
![]()
2.
Аддитивность.
Если область
![]() является объединением двух областей
является объединением двух областей
![]() и
и
![]() ,
не имеющих общих внутренних точек, то:
,
не имеющих общих внутренних точек, то:
![]()
3.
Интегрирование неравенств.
Если в любой точке
![]() выполняется неравенство
выполняется неравенство
![]() ,
и функции
,
и функции
![]() интегрируемы по области V,
то:
интегрируемы по области V,
то:
![]()
27. ВЫЧИСЛЕНИЕ ТРОЙНЫХ ИНТЕГРАЛОВ, ЗАМЕНА ПЕРЕМЕННЫХ
Допустим, что область T – простая в направлении оси Oz, т.е. любая прямая, проведённая параллельно оси Oz, пересекает границу области T не более чем в двух точках. Значит, область T ограничена снизу поверхностью z=z1(x,y), сверху поверхностью z=z2(x,y) и с боков – цилиндрической поверхностью с образующими, параллельными оси Oz. Тогда по аналогии с формулой вычисления объёмов цилиндрических тел при помощи двойных интегралов, можно получить:
 (2.2)
(2.2)
Здесь D – проекция области T на плоскость xOy. Если область D является простой в направлении оси Oy, то можно написать, что:
 (2.3)
(2.3)
Внешний интеграл обязательно (!) должен иметь постоянные пределы, а пределы второго интеграле зависит только от выбранной переменной, стоящей во внешнем.
Алгоритм вычисления тройных интегралов: 1) Сделать чертёж области интегрирования T; 2) Изобразить проекцию области T на выбранную координатную плоскость; 3) Расставить пределы интегрирования 4) Посчитать итог
Теорема о замене переменных в тройном интеграле:
]
в пространстве Ouvw
задана область G,
и пусть отображение
![]() преобразует эту область в область V
пространства
Oxyz.
Будем считать,
что отображение F
задаётся функциями
преобразует эту область в область V
пространства
Oxyz.
Будем считать,
что отображение F
задаётся функциями
![]() .
И пусть:
.
И пусть:
1) F взаимно однозначно отображает G на V;
2) Функции x(u,v,w), y(u,v,w), z(u,v,w) непрерывно дифференцируемы на G (имеют непрерывные частные производные);
3)
Якобиан
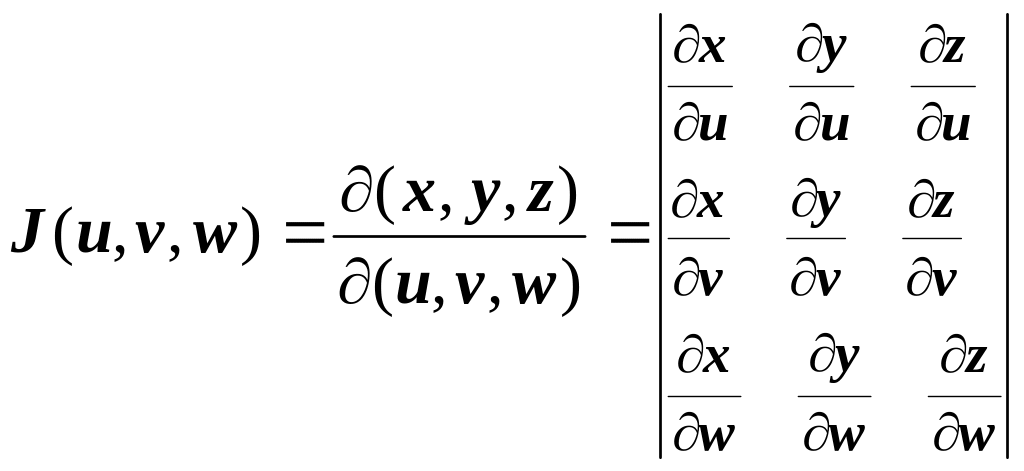 не обращается в нуль на G.
Тогда
не обращается в нуль на G.
Тогда
![]() .
.
28. Переход к сферическим и цилиндрическим координатам в тройном интеграле
Е
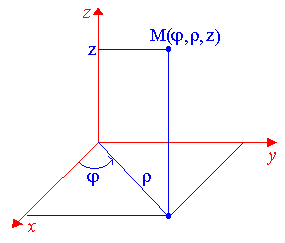 Рис.
2.5
Рис.
2.5 Рис.
2.8
Рис.
2.8
![]() (2.11)
(2.11)
Причём 02, 0+, –<z<+.
Модуль якобиана, соответствующий переходу от декартовых координат к цилиндрическим, равен:
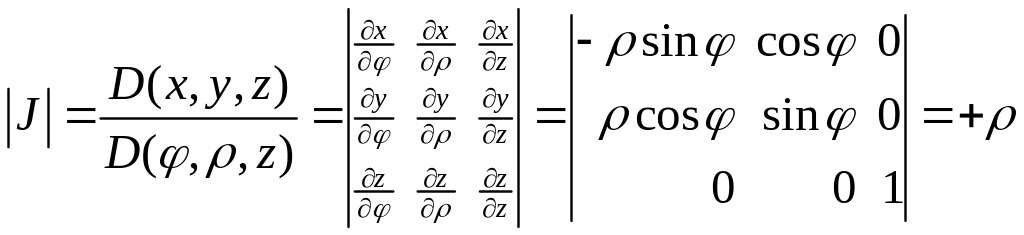 .
.
Т
 Рис.
2.6
Рис.
2.6
 (2.12)
(2.12)
Вычисление тройных интегралов в цилиндрических координатах приводится к однократным повторным интегралам на основании тех же принципов, что и в случае декартовых координат. Обычно порядок интегрирования такой:
 (2.13)
(2.13)
Сферическую систему координат удобнее использовать, если область интегрирования имеет центральную симметрию, т.к. тогда положение точки M определяется расстоянием от начала координат O, углом между осью Ox и проекцией радиус-вектора точки M на плоскость xOy, углом между осью Oz и радиус-вектором точки M. Из рисунка видно, что сферические координаты , , связаны с декартовыми координатами x,y,z соотношениями:
![]() (2.14)
(2.14)
Причём 02, 0, 0<+.
Модуль якобиана, соответствующий переходу от декартовых координат к сферическим, равен:
 .
.
Таким образом, формула перехода для тройных интегралов от декартовых координат к сферическим имеет вид:
 (2.15)
(2.15)
Вычисление тройных интегралов в сферических координатах приводится к однократным повторным интегралам на основании тех же принципов, что и в случае декартовых координат. Обычно порядок интегрирования следующий: , , . Тогда получаем:
 (2.16)
(2.16)
