13

ЛЕКЦИЯ 2

Замена переменных в двойном интеграле. Определитель Якоби. Вычисление двойных интегралов в полярной системе координат. Геометрические приложения двойных интегралов: вычисление площадей плоских фигур, объемов тел.

1.5. ЗАМЕНА ПЕРЕМЕННЫХ В ДВОЙНОМ ИНТЕГРАЛЕ

Трудность вычисления двойных интегралов связана не только со сложностью подынтегральной функции, но и с формой границы области интегрирования. Как мы видели, двойные интегралы проще всего вычисляются по прямоугольнику, стороны которого параллельны координатным осям; сложнее вычисляются по фигуре, ограниченной наклонными прямыми; еще сложнее, если граница области – кривая линия. В связи с этим и цель замены переменных в двойных интегралах несколько иная, чем цель замены переменной в определенном интеграле по отрезку. Там мы заботились только об упрощении подынтегральной функции, а область интегрирования при любой замене переменной оставалась отрезком. Упрощение подынтегральной функции – одна из целей замены переменных в двойном интеграле. Другая цель – упрощение области интегрирования.

Предположим, что с помощью формул

x = x(u,v), y = y(u,v) (1.8)

мы переходим к новым переменным u и v. Будем считать, что u и v определяются из (1.8) единственным образом:

u = u(x,y), v = v(x,y). (1.9)

Это означает, что каждой точке M(x,y) из области D на плоскости xOy ставится в соответствие одна и только одна точка M^*(u,v) из области G на плоскости uO'v. Другими словами, между областями D и G существует взаимно однозначное соответствие.

Пусть функция f(x,y) непрерывна в некоторой замкнутой ограниченной области D. Тогда для функции f(x,y) существует двойной интеграл

. (1.10)

При сделанных выше предположениях можно доказать, что

если функции (1.8) имеют в области D непрерывные частные производные первого порядка и если определитель Якоби (якобиан):

(1.11)

отличен в области G от нуля, то для интеграла (1.10) справедлива формула замены переменных:

. (1.12)

Пример 1.7. Вычислить интеграл

г

а б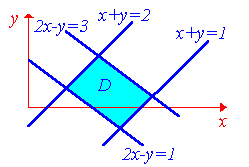

Рис. 1.12

де D – параллелограмм, ограниченный прямыми: x+y=1, x+y=1, 2x–y=1, 2x–y=3 (рис. 1.12).

Решение. Непосредственное вычисление данного интеграла достаточно громоздкое, т.к. для сведения его к повторному необходимо область D разбить на три части и затем вычислить соответственно три интеграла. Однако простая замена переменных

x+y=u, 2x–y=v (1.13)

позволяет значительно упростить решение. Прямые x+y=1 и x+y=2 в системе координат xOy (рис. 1.12а) переходят в прямые u=1 и v=2 в системе координат uO'v (рис. 1.12б), а прямые 2x–y=1 и 2x–y=3 в прямые v=1 и v=3. Параллелограмм D взаимно однозначно преобразуется в прямоугольник G, который является более простой областью интегрирования. Осталось вычислить якобиан. Для этого выразим x и y через u и v из равенств (1.13): , . Следовательно

.

По формуле (1.12) окончательно получаем

.

Отметим, что величины u и v можно рассматривать как координаты (отличные, вообще говоря, от декартовых) точек области D. Так как координатные линии, в соответствие с формулами (1.8), будут, в общем случае, кривыми (а не прямыми, как в случае декартовых координат), то величины u и v называют криволинейными координатами точек области D.

1.6. ВЫЧИСЛЕНИЕ ДВОЙНЫХ ИНТЕГРАЛОВ В ПОЛЯРНОЙ СИСТЕМЕ КООРДИНАТ

Наиболее употребительная система координат на плоскости – это полярные координаты. Они связаны с декартовыми координатами x и y равенствами:

(1.14)

где 0, 0<2. (Повторите тему: "Полярная система координат").

Пусть рассматривается двойной интеграл

,

г

а б

Рис. 1.13

де D – область, изображенная на рис. 1.13а. Разобьем эту область на части посредством координатных линий полярной системы, т.е. линий =const и =const. Каждый элементарный участок (рис. 1.13б) можно принять приближенно за прямоугольник со сторонами _i и _i_j. Тогда площадь элементарного участка будет приближенно равна

.

Следовательно, интегральную сумму для двойного интеграла в полярной системе координат можно записать в виде

.

Переходя к пределу, т.е. увеличивая число разбиений до бесконечности (при этом ), получим двойной интеграл в полярной системе координат

. (1.14)

Если область интегрирования D является простой в осевом направлении, т.е. любой луч, выходящий из центра координат, пересекает границу области интегрирования не более чем в двух точках, то двойной интеграл можно записать в виде повторного:

. (1.15)

Теперь проинтерпретируем полученный результат с точки зрения замены переменных. Вычислим якобиан перехода от декартовых координат к полярным, т.е. якобиан преобразования (1.14). Как и следовало ожидать, получим

Таким образом, формулу (1.14) можно было получить непосредственно из общей формулы замены переменных в двойных интегралах.

Отметим, что переход от декартовых координат к полярным во многих случаях является целесообразным, если подынтегральная функция или уравнения границы области интегрирования содержат сумму x²+y², т.к. данная сумма в полярных координатах принимает вид (cos)²+(sin)2=². Например, если область интегрирования имеет вид четверти круга x²+y²=1, x0, y0, то "с точки зрения" полярной системы координат эта область будет иметь прямоугольный в

а б

Рис. 1.14

ид.

П

Рис. 1.15

ример 1.8. Вычислить интеграл

где .

Решение. Перейдем в полярную систему координат x=sin, y=cos, x²+y²=². Тогда уравнение границы области D примет вид =2cos. Это есть уравнение окружности (рис. 1.15). Здесь  изменяется от –/2 до /2, а  от 0 до окружности =2cos. Таким образом, получаем

1.7. ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ДВОЙНЫХ ИНТЕГРАЛОВ

1.7.1. Вычисление площадей плоских фигур

К

Рис. 1.16

ак было установлено, площадь области интегрирования D может быть вычислена с помощью двойного интеграла по формуле

(1.16)

Эта формула более универсальна, чем соответствующая формула, выражающая площадь криволинейной трапеции с помощью определенного интеграла, т.к. данная формула применима не только к криволинейным трапециям, но и к фигурам, расположенным произвольно по отношению к координат­ным осям. В частности, если фигура ограничена двумя кривыми y=f₁(x) и y=f₂(x) и двумя прямыми x=a и x=b (см. рис. 1.16), то получим формулу

.

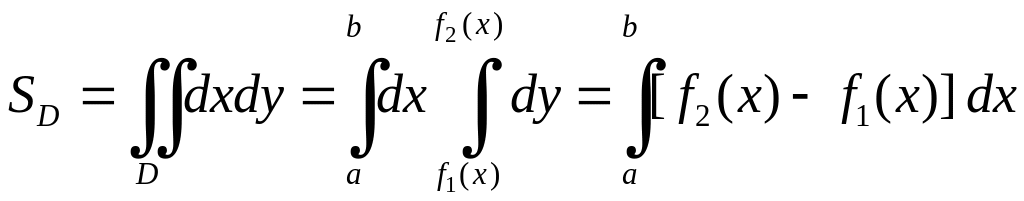Это есть формула вычисления площадей плоских фигур при помощи определенных интегралов.

П

Рис. 1.17

ример 1.9. Вычислить площадь фигуры ограниченной линиями x²=y, x²=4y, y=4.

Решение. Изобразим данную фигуру (рис. 1.17). Видно, что полученная фигура состоит из двух одинаковых областей: D₁ и D₂. следовательно

.

Интегрирование во внешнем интеграле будем производить по переменной y (в противном случае область интегрирования пришлось бы разбивать на две части). Тогда переменная y будет изменяться от 0 до 4, а переменная x, соответственно, от параболы до параболы . В результате получаем

.

В случае полярной системы координат площадь плоской фигуры вычисляется при помощи интеграла

Рис.1.18

(1.17)

В частности, если область интегрирования имеет вид, изображенный на рис. 1.18, то получим

.

Это есть известная формула вычисления площадей при помощи определенных интегралов в полярной системе координат.

П

Рис. 1.19

ример 1.10. Вычислить площадь фигуры, ограниченной линией .

Решение. Запишем уравнение линии в полярной системе координат

,

т.е.

.

Построим эту линию (рис. 1.19). Поскольку полученная формула симметрична относительно осей Ox и Oy, то достаточно вычислить площадь четвертой части этой фигуры, а затем умножить полученный результат на 4:

.

1.7.2*. Вычисление объемов тел

Криволинейным цилиндром с основанием D, лежащим в плоскости xOy, называется тело T, ограниченное этим основанием, некоторой поверхностью z=f(x,y) и боковой цилиндрической поверхностью (рис.1.20).

О

Рис. 1.20

бъем V такого цилиндра определяется следующим образом: разбиваем основание D на определенное количество непересекающихся частей D. Затем разбиваем весь цилиндр T на цилиндрообразные части T_i, основания которых являются D_i. Очевидно, что объем цилиндра T равен сумме объемов его частей T_i. Для нахождения объема части T_i выберем в D_i некоторую точку (x_i,y_i) и заменим часть T_i с криволинейным верхним основанием цилиндром с постоянной высотой, равной f(x_i,y_i) и тем же основанием D_i. Примем объем цилиндра T_i приближенно равным f(x_i,y_i)s_i (s_i – площадь D_i). Тогда сумма

.

приблизительно равняется объему цилиндра. Ясно, что сумма _n представляет собой интегральную сумму функции f(x,y) по области D. В результате мы получаем, что двойной интеграл представляет собой объем соответствующего криволинейного цилиндра (в этом заключается геометрический смысл двойного интеграла).

Пример 1.11*. Найти интеграл , рассматривая его как предел интегральных сумм.

Решение. Разобьем область интегрирования на квадраты прямыми

и вычислим значение подынтегральной функции в правом верхнем углу каждого квадрата. Составим интегральную сумму

,

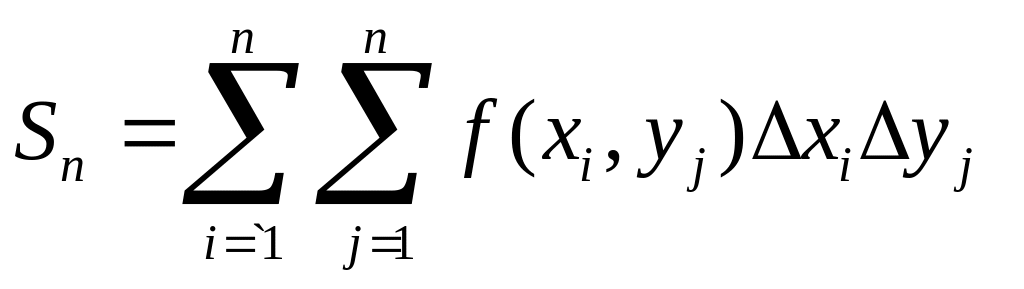где . Тогда

.

Пример 1.12. Найти объем тела V, который получается в результате пересечения цилиндра и сферы (рис. 1.21).

Решение. Объем данного тела находим по формуле

Рис. 1.21

,

где функция определена в круге, задаваемом неравенством

.

Итак, получаем

.

Переходя к полярным координатам, приходим к интегралу

.

Здесь – уравнение границы упомянутого круга в полярных координатах.