Ал. занятие3

Пространство решений

однородной системы линейных уравнений

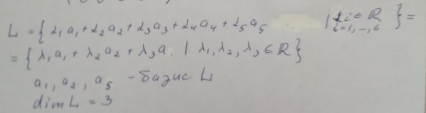---------------------------------------------------------------------------------------------------------------------Однородной системой линейных уравнений называется система, правая часть которой равна нулю:

Матричный вид однородной системы:  Ax=0.

Однородная система в с е г д а  с о в м е с т н а, поскольку любая однородная линейная система имеет по крайней мере одно решение:

x₁=0 , x₂=0 , ..., x_n=0.

Рассмотрим однородную систему линейных уравнений:

,

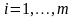
Пусть , - два решения однородной системы. Тогда , 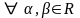также решение этой системы. Таким образом, множество всех решений однородной системы есть линейное пространство, которое является подпространством . Размерность этого пространства равна n-r , где r ранг матрицы системы. Базис образуют любые n-r линейно независимых частных решения системы.

Базис пространство решений однородной системы линейных уравнений называют еще фундаментальной системой решений.

Пример: Найти размерность и базис пространства решений однородной системы линейных уравнений:

.

Применяя метод Гаусса, решим систему:

, .

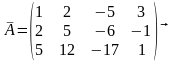
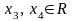Размерность пространства решений системы n-r = 4 – 2 = 2.

Далее положим сначала 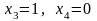, а затем .

Получим два частных решения системы , ,

образующих базис пространства решений однородной системы линейных уравнений.

или

Найти размерность и базис пространства решений однородной системы линейных уравнений:

Дома: №730, 1313