
Ал.занятие2. Базис и размерность линейного пространства
.docxБазис и размерность линейного пространства.
Опр.: Пусть линейное пространство V содержит набор из n линейно независимых векторов, а любой набор из (n +1) –го вектора этого пространства линейно зависим.
Тогда говорят, что размерность пространства V равна n.
Обозначают dimV=n и называют пространство n – мерным.
Опр.: Пусть линейное пространство V имеет размерность n.
Пусть
 - упорядоченная система n
линейно независимых векторов из V.
Тогда система векторов
называется базисом пространства
V.
- упорядоченная система n
линейно независимых векторов из V.
Тогда система векторов
называется базисом пространства
V.
Теорема: Каждый вектор х линейного пространства V можно представить и притом единственным способом в виде линейной комбинации векторов базиса.
Если
-
базис пространства V и
х = ,
х
,
х ,
,
то
числа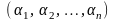 -
координаты вектора х в базисе
.
-
координаты вектора х в базисе
.
Пример:
Даны векторы
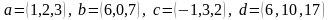 .
Покажем, что векторы
.
Покажем, что векторы
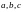 образуют базис
образуют базис
 ,
и найдем координаты вектора
,
и найдем координаты вектора
 в этом базисе.
в этом базисе.
Составим матрицу из векторов и найдем ее определитель, (можно рассматривать ранг этой матрицы).
detА= ,
следовательно, rangA=3, а значит, векторы
линейно независимы и, т.к. dim
=3,
то
образуют базис.
,
следовательно, rangA=3, а значит, векторы
линейно независимы и, т.к. dim
=3,
то
образуют базис.
Или

Для нахождения координат вектора в базисе рассмотрим равенство
= .
.

Итак,
 Имеем
=
Имеем
= ,
,
т.е. (2,1,2) координаты вектора в базисе .
Переход к новому базису
Базис в пространстве определен неоднозначно. Рассмотрим, как изменяются координаты вектора при переходе от одного базиса к другому.
Пусть в линейном пространстве V
имеются два базиса: старый
и новый
 .
Каждый из векторов нового базиса можно
выразить в виде линейной комбинации
векторов старого базиса:
.
Каждый из векторов нового базиса можно
выразить в виде линейной комбинации
векторов старого базиса:

Полученная система означает, что переход
от старого базиса
к новому
задается матрицей перехода Т= ,
в которой по столбцам стоят координаты
новых базисных векторов в старом базисе.
Причем,
,
в которой по столбцам стоят координаты
новых базисных векторов в старом базисе.
Причем,

Пусть произвольный вектор х
имеет координаты
 в старом базисе и координаты
в старом базисе и координаты
 в новом базисе, тогда
в новом базисе, тогда
 =Т
=Т или
=
или
= .
.
Пример: Найдем координаты вектора
х =
 в базисе
в базисе
 ,
если
,
если

Матрица перехода Т= ,
найдем
,
найдем
 .
.

 =7,
=7,
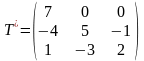 ,
тогда
,
тогда
=
 .
Имеем,
.
Имеем,
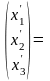
 =
=
 =
= .
.
Таким образом, (2,-2,1) - координаты вектора х в базисе .






