
алг 1.2. Обратная матрица
.docxОбратная матрица
Матрица
 называется обратной
по отношению к квадратной матрице А,
если
называется обратной
по отношению к квадратной матрице А,
если
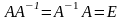 .
.
Обратная матрица
существует тогда и только тогда, когда

Обратная матрица
может быть найдена по формуле
= ,
,
где
 -
присоединенная матрица:
-
присоединенная матрица:
= ,
т.е. матрица, элементы которой есть
алгебраические дополнения
,
т.е. матрица, элементы которой есть
алгебраические дополнения
 элементов матрицы, транспонированной
к А.
элементов матрицы, транспонированной
к А.
Пример:
Найти
обратную матрицу для матрицы ![]()
Последовательность действий удобно разложить по пунктам.
Сначала находим определитель матрицы.
![]()
В том случае, если определитель матрицы равен НУЛЮ – обратной матрицы НЕ СУЩЕСТВУЕТ.
В
рассматриваемом примере, как выяснилось, ![]() ,
а значит, всё в порядке.
,
а значит, всё в порядке.
Находим - присоединенную матрицу, составленную из алгебраических дополнений А, (алгебраические дополнения строк записываются в столбцы ).





Имеем

Вспоминаем формулу = Таким образом, обратная матрица:
![]()
Проверка:

Получена единичная матрица .
Таким образом, обратная матрица найдена правильно.
Пример:
Найдем матрицу, обратную к данной матрице
А= .
.
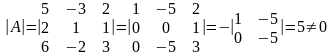
 5,
5,
 0,
0,
 -10,
-10,
 5,
5,
 3,
3,
 -8,
-8,
 -5,
-5,
 -1,
-1,
 11.
11.
 ,
=
,
=
 =
= .
.
Свойства обратной матрицы:
1)
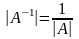 ,
2)
,
2)
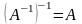 ,
3)
,
3)
 ,
4)
,
4)
 ,
5)
,
5)
 .
.
Матричные уравнения.
Типовое
матричное уравнение состоит, как правило,
из нескольких матриц и неизвестной
матрицы ![]() ,
которую предстоит найти. То есть, решением
матричного уравнения является матрица.
,
которую предстоит найти. То есть, решением
матричного уравнения является матрица.
Простейшие уравнения имеют вид:
![]() либо
либо ![]() ,
где
,
где ![]() – известные матрицы.
– известные матрицы.
.
Для
того, чтобы разрешить данное уравнение
относительно
,
умножим обе его части на ![]() слева (здесь
и далее предполагаем, что обратная
матрица существует):
слева (здесь
и далее предполагаем, что обратная
матрица существует):
![]()
Произведение матриц не перестановочно, поэтому критически важно, с какой стороны проводить умножение.
![]() ,
поэтому:
,
поэтому:
![]()
Имеем
![]()
.
Умножаем
обе части уравнения на
справа:
![]()
![]() ,
получаем:
,
получаем:
![]()
![]()
Пример: Решить матричное уравнение, выполнить проверку
![]()
Уравнение уже имеет вид
Для
разрешения уравнения относительно ![]() умножим
обе его части на
умножим
обе его части на ![]() слева:
слева:

Из
условия известны матрицы ![]() ,
однако, обратной матрицы
мы
не знаем. Придётся её найти. Обратную
матрицу найдем по формуле
=
,
однако, обратной матрицы
мы
не знаем. Придётся её найти. Обратную
матрицу найдем по формуле
=
![]()

Таким
образом, обратная матрица:
![]()
На
финише проводим матричное умножение и
получаем решение:
![]()
Ответ: ![]()
Метод обратной матрицы решения систем линейных уравнений.
Матричный метод применяется для решения систем линейных уравнений, в которых число неизвестных переменных равно числу уравнений и определитель основной матрицы отличен от нуля.
Пусть
нам требуется решить систему линейных
уравнений вида
 где x1,
x2,
…, xn –
неизвестные переменные, ai
j , i
= 1, 2, …, n,
где x1,
x2,
…, xn –
неизвестные переменные, ai
j , i
= 1, 2, …, n,
j = 1, 2, …, n – числовые коэффициенты, b1, b2, …, bn - свободные члены.
В матричной форме система имеет вид АХ=В, где
А= ;
Х=
;
Х= ;
В=
;
В= .
.
Матричный метод решения системы линейных уравнений:
Если система
квадратная и
 ,
то система имеет единственное решение
,
то система имеет единственное решение
 .
.
Пример:
Решим систему линейных уравнений

матричным методом
А= ;
Х=
;
Х= ;
В=
;
В= .
.
 =
= =-2;
=-2;
 -11,
-11,
 -13,
-13,
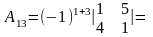 -19,
-19,
 -8,
-8,
 -10,
-10,
 -14,
-14,
 7,
7,
 9,
9,
 13.
13.
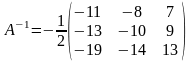 ;
;
= =
= ,
,
т.е.
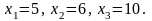
Ответ: ( 5, 6, 10 )
Дома: № 862, 864
