
Ангем Определения 1 курс 2 сем
.docx
1.Уравнение
плоскости. Вектор нормали к плоскости.


2.
Канонические уравнения прямой в
пространстве
 3.
Расстояние от точки до плоскости
3.
Расстояние от точки до плоскости

4.Преобразование
координат вектора при изменении базиса.
Матрица перехода и их свойства


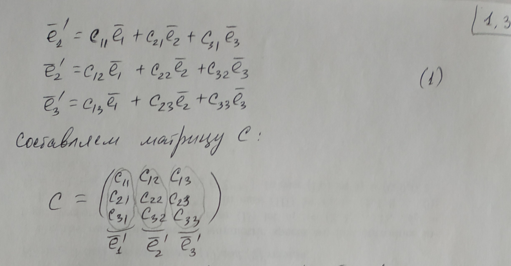
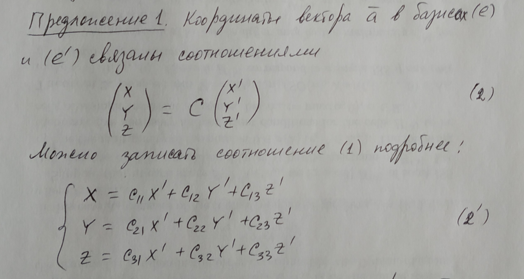
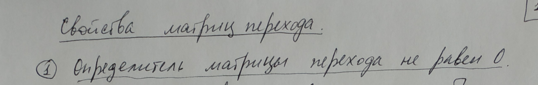
 5.Преобразование
координат точек при изменении системы
координат. Параллельный перенос системы
координат. Поворот системы координат
5.Преобразование
координат точек при изменении системы
координат. Параллельный перенос системы
координат. Поворот системы координат



6.Эллипс. Каноническая система координат. Уравнение эллипса. Эксцентриситет и директрисы эллипса.


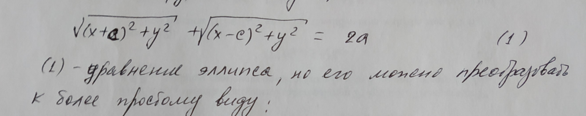
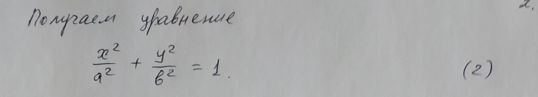
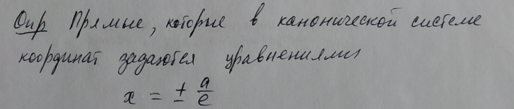
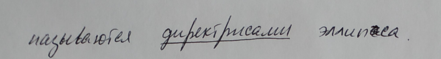

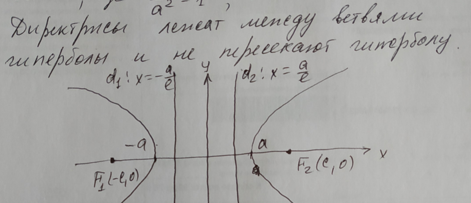
7.
Гипербола. Каноническая система
координат. Уравнение гиперболы.
Эксцентриситет, директрисы и асимптоты
гиперболы.



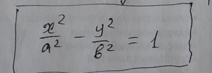


 8.
Парабола. Каноническая система координат.
Уравнение параболы.
8.
Парабола. Каноническая система координат.
Уравнение параболы.
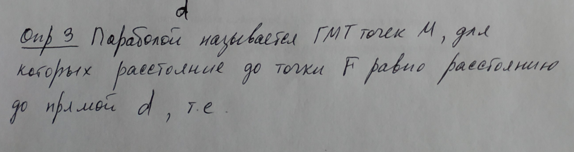



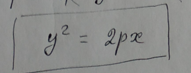 9.
Линии второго порядка и их матрицы
9.
Линии второго порядка и их матрицы



10.
След матрицы и его свойства

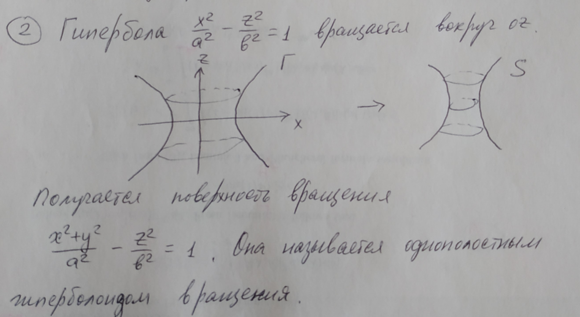
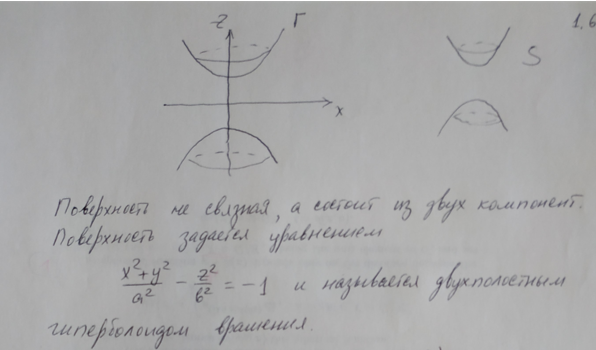
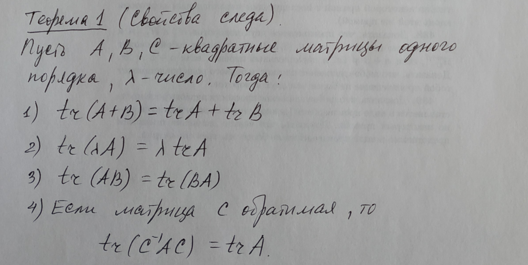 11.Поверхности
вращения и их уравнения
11.Поверхности
вращения и их уравнения



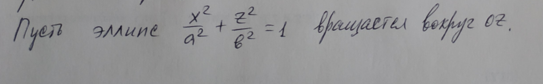


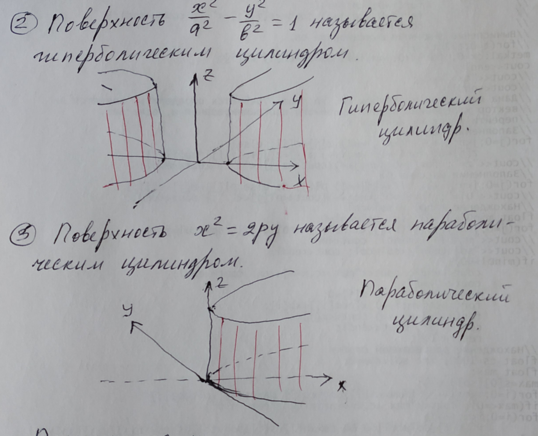
 11.
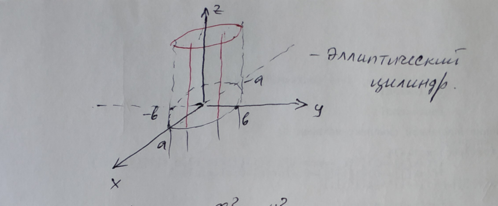
Циллиндрические поверхности и их
уравнения
11.
Циллиндрические поверхности и их
уравнения



13.
Конические поверхности и их уравнения


 14.
Гиперболоиды и параболоиды
14.
Гиперболоиды и параболоиды



15. Прямолинейные образующие поверхности
16. Векторные пространства и подпространства. Задание подпространств системой уравнений



17.
Аффинные пространства. Примеры аффинных
пространств

 18.
Аффинная система координат. Координаты
точек и векторов в аффинной система
координат.
18.
Аффинная система координат. Координаты
точек и векторов в аффинной система
координат.


 19.
К-мерные плоскости в аффинном пространстве
и задание их системами уравнений.
Гиперплоскости.
19.
К-мерные плоскости в аффинном пространстве
и задание их системами уравнений.
Гиперплоскости.




20. Скалярное произведение в векторном пространстве. Модуль вектора. Ортонормированный базис. Неравенство Коши – Буняковского.
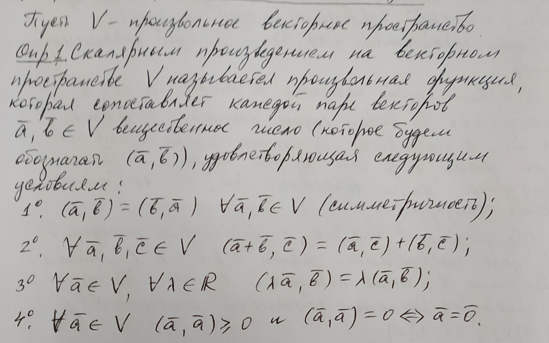
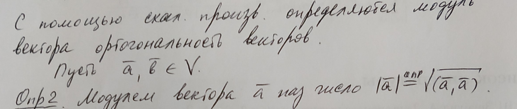

 21.
Аффинные евклидовы пространства.
Расстояние между точками в аффинном
евклидовом пространстве.
21.
Аффинные евклидовы пространства.
Расстояние между точками в аффинном
евклидовом пространстве.

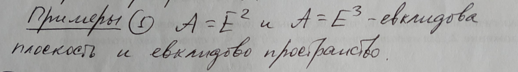
 22.
Определение векторного пространства.
Примеры векторных пространств.
Пространство Rn.
22.
Определение векторного пространства.
Примеры векторных пространств.
Пространство Rn.



23. Линейные комбинации векторов. Линейная зависимость и независимость.

24. Базис пространства. Координаты вектора относительно базиса. Размерность векторного пространства.


2 5.
Определение и свойства векторного
произведения. Вычисление векторного
произведения в координатах.
5.
Определение и свойства векторного
произведения. Вычисление векторного
произведения в координатах.
2

 6.
Смешанное произведение векторов и его
свойства. Вычисление смешанного
произведения в координатах.
6.
Смешанное произведение векторов и его
свойства. Вычисление смешанного
произведения в координатах.
