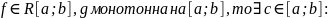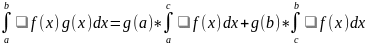7. Суммы Дарбу и их свойства.
f R[a;b] => f ограничена на [a;b] Далее будем полагать, что f ограничена на [a;b] Введем обозначения: mx = inf f(x) -минимум x [xk;xk+1]
Mx
= sup f(x) -максимум x
[xk;xk+1]
Образуем
следующие суммы:
s(T)
=
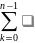mk*Δxk
- нижняя
сумма Дарбу
S(T)
=
Mk*Δxk
-
верхняя
сумма Дарбу
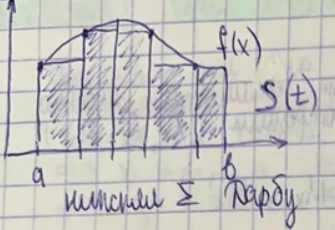
Свойства сумм Дарбу:
10
Для
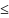
каждого фиксированного 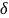T s(T)
(T)
S(T)
20 Если к разбиению добавить новые точки, то нижняя сумма Дарбу может только увеличиться, а верхняя - только уменьшиться
30 Для каждого разбиения T1 и T2 S(T1) S(T2)
40 s(T1) I* (т.к. sup - макс) I*(т.к. s S) S(T2) (т.к. I* - inf - мин)
где I* - верхний интеграл Дарбу infT S(T);
I* - нижний интеграл Дарбу supT s(T).
Лемма: Если x1 и x2 - ограничены, то
sup(x1 + x2) = sup(x1) + sup(x2)
inf(x1 + x2) = inf(x1) + inf(x2)
50
s(T)
= inf(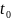
...
)
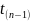Δ(T)
S(T) = sup( ... ) Δ(T)
8. Критерий интегрируемости по Риману.
Теорема(из
лекций): f
R
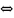S(T)
- s(T)
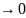(при
)
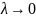(где диаметр
разбиения)
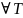
Следствия(тоже из лекций): где I* - верхний интеграл Дарбу; I* - нижний.
1. Если f R, то I* = I* =
2.
Если
f
R
[a, b], то S(T) и s(T)
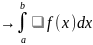(при х
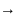0)
3.
Рассмотрим
S(T) - s(T) =
(
-
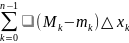
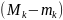обозначим wk
- колебание f на [xk,
xk+1],
что по сути разность между наибольшим
и наименьшим значением функции)
f
R
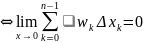
Теорема
(критерий интегрируемости по Риману):
пусть
функция f ограничена на отрезке [a;b]. Для
того чтобы f была интегрируемой на этом
отрезке, необходимо и достаточно, чтобы
было выполнено равенство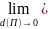
(
)
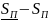= 0. Это равенство означает, что для любого
положительного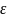
найдется
такое положительное
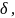что для каждого разбиения П, диаметр
которого d(П) <
,
справедливо неравенство
<
Короче я хз, там где у второй S должно быть нижнее подчеркивание, но оно не работает(
9. Достаточные условия интегрируемости по Риману.
Теорема 1) Если функция f(x) непрерывна на [a;b], то она интегрируема по риману на этом отрезке( f ∈ R[a;b]).
Теорема 2) Если функция f(x) ограничена и монотонна на отрезке [a;b], то она интегрируема по риману на этом отрезке(f ∈ R[a;b]).
10. Свойства интеграла Римана.
Если
a>b, то по определению считают, что
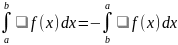
10
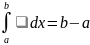
20 Линейность интеграла Римана
Если f, g R [a;b], то
а) f+g R [a; b]
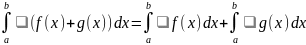
б) k - const
kf [a; b]
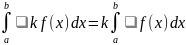
30
Если
a < b, f
R [a, b], тогда
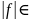R
[a; b] и
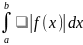
40 Если f, g R [a; b], то f*g R [a; b]
50
Если
a < b, f
R
[a; b] и
f(x)
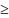0,
то
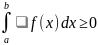
60
Если
a < b, f, g
R[a;
b] и
f(x)
g(x), где
x
[a;
b], тогда
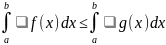
70
Если
f
R
[a; b], [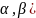
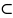[a;
b], то
f
R[
80 Адаптивность интеграла
Если f интегрируема по Риману на большем из отрезков [a; b], [a; c], [c, b], то
90
Если a < b, f
,
f(x)
0
на [a; b] и
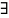x0
[a; b], в которой f непрерывна и
f(x0)
> 0, тогда
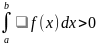
100 Теорема о среднем
Если
f
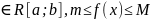(где
m,M - некоторые числа) на x
,
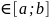то
а)
:
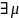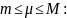
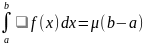
b) Если дополнительно f непрерывна на [a; b], то с :
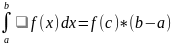
Геометрический смысл:
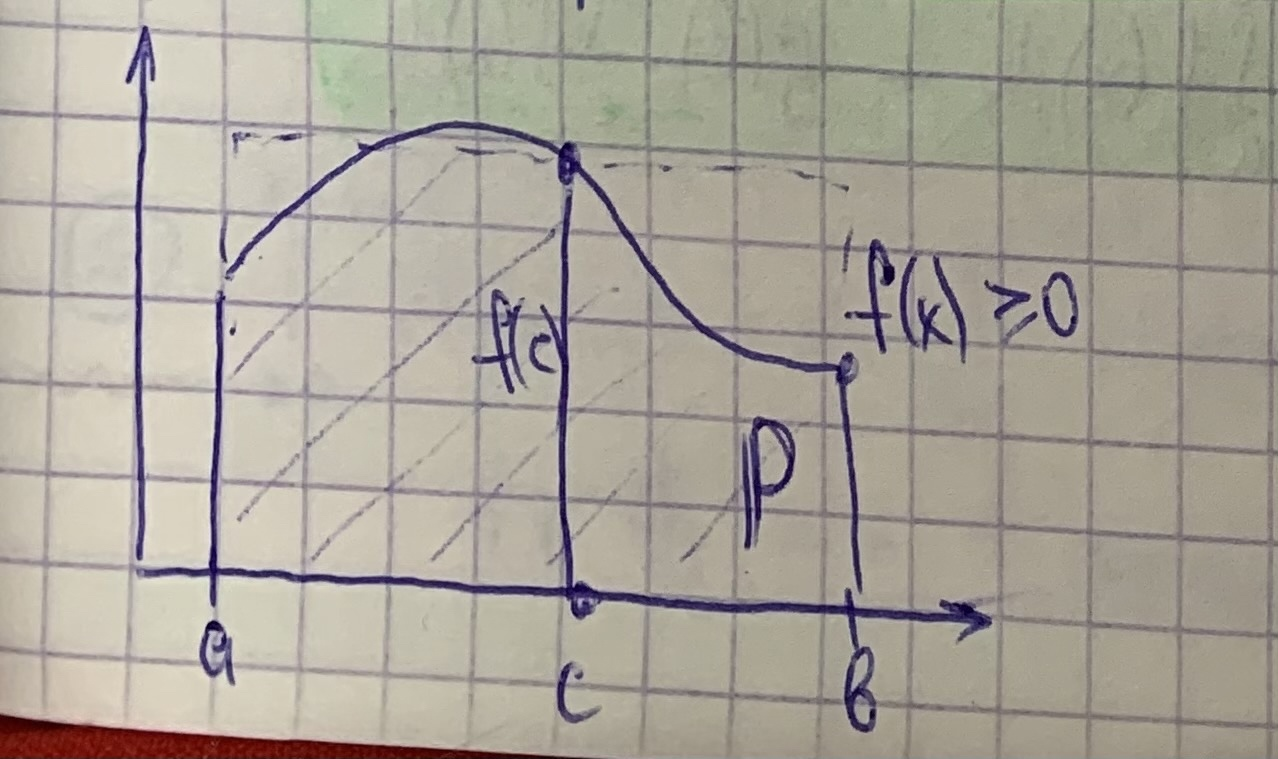
110 Вторая теорема о среднем:
Если
