4. Установившийся режим крашения

В этом режиме затраты теплоты обусловлены лишь потерями в окружающую среду. Порядок расчета этой статьи теплового баланса остается прежним, с учетом того, что в качестве температуры жидкости используется температура, до которой был разогрет раствор. Поскольку в этом режиме система обогревается глухим паром, его масса определяется по тому же уравнению, что и разделе 3. Расход пара рассчитывается также как и ранее по массе пара и продолжительности процесса.

5. Расхолаживание красильного бака водой

Вода для расхолаживания подается в змеевик, площадь поверхности которого рассчитана в предыдущем разделе. И здесь ставится задача расчета расхода воды.

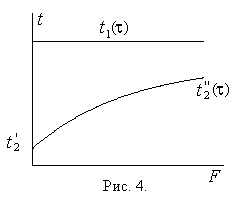На рис. 4 представлен температурный график змеевикового теплообменника при расхолаживании. Температураt₁горячего теплоносителя (раствора) остается постоянной по поверхности, но изменяется во времени (уменьшается). Температура холодного теплоносителя на входе в теплообменникt₂поддерживается постоянной, а на выходе из негоt₂изменяется во времени.

Дифференциальная форма уравнения теплового баланса имеет вид

(34)

где среднее по поверхности теплообмена значение температурного напора в произвольный момент времени. Здесь и далее горизонтальная черта сверху будет использоваться для характеристики средних по поверхности величин.

Второй член уравнения (34) характеризует теплоту, перенесенную за счет теплопередачи, третий – теплоту, полученную охлаждающей водой, и четвертый – теплоту, отданную раствором. Величина (Mc)_определяется теми же выражениями (26), (27), что и ранее.

Интегральная форма уравнения теплового баланса для всего периода расхолаживания будет иметь вид

(35)

где C₂ =G₂c₂– расходная теплоемкость холодного теплоносителя.

Количество теплоты, передаваемой в процессе расхолаживания, рассчитывается по последнему члену в уравнении (35). Для нахождения расхода охлаждающей воды необходимо найти величину t₂. Вычислим вначале среднее по поверхности значение температурного напора для любого момента времени. В соответствии с графиком рис. 4 больший температурный напор равенt₁t₂, а меньшийt₁t₂, и искомое значение среднего по поверхности температурного напора, равное его среднелогарифмическому значению записывается как

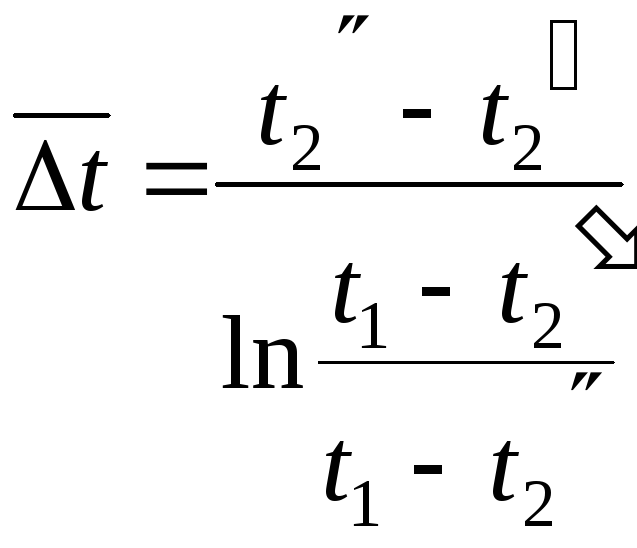(36)

Подставляя полученное значение в уравнение, характеризующееся вторым знаком равенства в формуле (34), после простых преобразований получим

t₂  t₂ = (t₁  t₂)(1exp(N₂)), (37)

где через N₂обозначено число единиц переноса

N₂ = kF/C₂. (38)

В уравнении (37) все члены, кроме t₂иt₁, не зависят от времени. Поэтому результат его осреднения по времени можно представить как

t₂  t₂ = (t₁  t₂)[1exp(N₂)]. (39)

Для нахождения величины t₁, входящей в формулу (39) воспользуемся дифференциальным уравнением, определяемым последним равенством в (34), предварительно заменив в немt₂ t₂при помощи формулы (37). Интегрирование полученного дифференциального уравнения метолом разделения переменных и потенцирование полученного результата позволяют получить зависимость температуры раствора от времени

t₁  t₂ = (t_1н  t₂)exp{C₂ [1exp(N₂)]} (40)

Проведем процедуру осреднения во времени температуры раствора, аналогично тому, как это было сделано в разделе 3. Из полученного результата с помощью уравнения (40) исключим величину C₂[1exp(N₂)], то дает

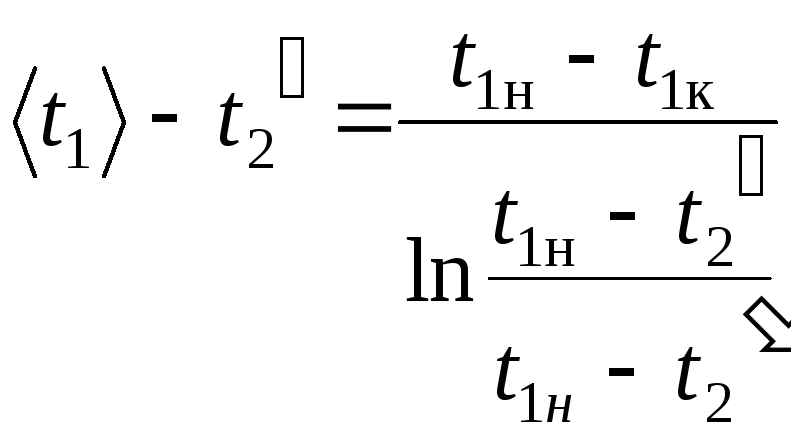(41)

Подставим уравнение (39) в уравнение (35) со вторым знаком равенства и получим

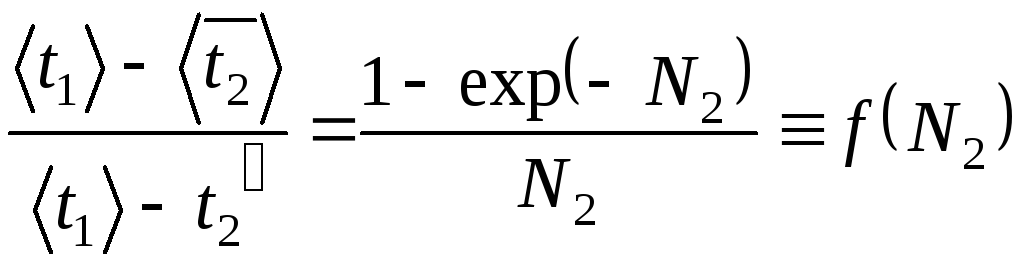(42)

График функции f(N₂), определяемый правой частью уравнения (42), показан на рис. 5. Чтобы найти величинуС₂по формуле (38), по графику рис. 5 следует определить значениеN₂. Но для этого необходимо предварительно значение температурыи величину коэффициента теплопередачи . Эта задача решается в процессе итераций следующим образом. Предварительно по известному количеству теплоты, площади и времени вычисляется средняя плотность теплового потока

q = Q^*/(F)

Далее реализуется итерационная цепочка

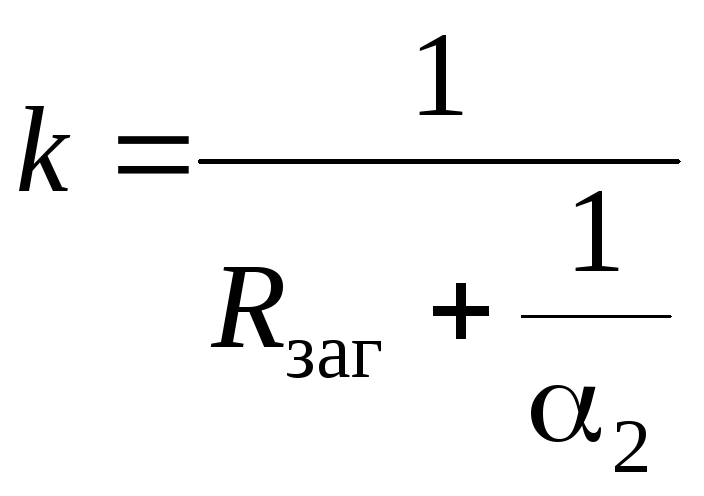(43)

(44)

q = (t₁  t_c)/R_заг (45)

Для реализации этой цепочки можно использовать следующую последовательность вычислений. Задаются значением коэффициента теплоотдачи ₂по порядку величины. Вычисляют коэффициент теплопередачи по формуле (43), из уравнения (44) находятсреднюю по поверхности и времени температ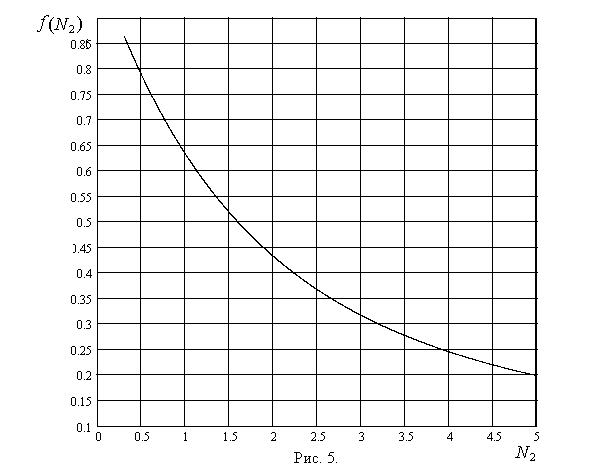уру охлаждающей воды, а по формуле (45) среднюю по времени и поверхности температуру стенкиt_с. Эти две последние температуры используются при вычислении коэффициента теплоотдачи₂по уравнению подобия для свободной конвекции, что позволяет найти уточненное значение коэффициента теплопередачи и т.д. Сходимость итераций проверяется по величине коэффициента теплопередачиk.

После того, как найдена в процессе итераций температура , левая часть уравнения (42) легко рассчитывается и тем самым определяется функцияf(N₂), по величине которой при помощи графика рис. 5 определяется величинаN₂. Далее по найденному значению коэффициента теплопередачи по уравнению (38) рассчитывают величинуС₂, а по ней – расход воды.

При необходимости получения более точных результатов следует численно решать нелинейное уравнение (42) относительно N₂.