Лабораторная работа 6

Синтез и анализ кулачкового механизма

Синтез кулачкового механизма (рис. 22) выполняем по заданному закону движения толкателя и допускаемым углам давления. Основные размеры механизма - минимальный радиус-векторкулачка и эксцентриситетдолжны быть такими, чтобы во всех положениях механизма углы давленияне превышали допускаемого значения

.

В кулачковых механизмах с поступательно движущимся толкателем максимальное значение угла давления приближенно соответствует положению механизма, при котором аналог скорости имеет максимальное значение. Для определения основных размеров кулачкового механизма используем упрощенный график перемещения толкателя в функции его аналога скорости. На этом графике (рис. 23) показаны только максимальные значения аналога скорости на фазах подъемаи опускания. По осив соответствии с направлением вращения кулачка откладываются максимальные аналоги скоростина фазе подъема ина фазе опускания , а по осиперемещение толкателя. Максимальные значения аналогов скорости возникают в тех положениях механизма, при которых толкатель находится на половине хода. Через точкиипод допустимыми углами давления проведены линии, точкапересечения которых дает положение центра вращения кулачка. При этом получаем механизм с углами давления не превышающими допустимое значение.

Рис.25. Схема кулачкового механизма

Координаты точкиопределяются в результате пересечения двух прямых, проходящих через точкии(рис.26). Уравнения прямых

(33)

Решением системы линейных уравнений являются координаты точкицентра вращения кулачка. В этом уравнении

угловые коэффициенты прямых линийкоординаты точеки.

Минимальный радиус-вектор центрового профиля кулачка и эксцентриситет определяются по формулам

, . (34)

При решении системы линейных уравнений в системе Mathcad Pro можно использовать функцию _. Порядок использования этой функции изложен в лабораторной работе 1. В работе рассмотрим символьное решение системы линейных уравнений (рис.27).

Чтобы решить систему уравнений в символьном виде, необходимо выполнить следующие действия:

• напечатать слово , это слово сообщающее программеMathcad, что далее следует система уравнений;

• напечатать ниже слова уравнения системы в любом порядке. Знак равенства в уравнениях является знаком логического равенства. Для его ввода используется палитра символов или сочетание клавиш;

• напечатать функцию 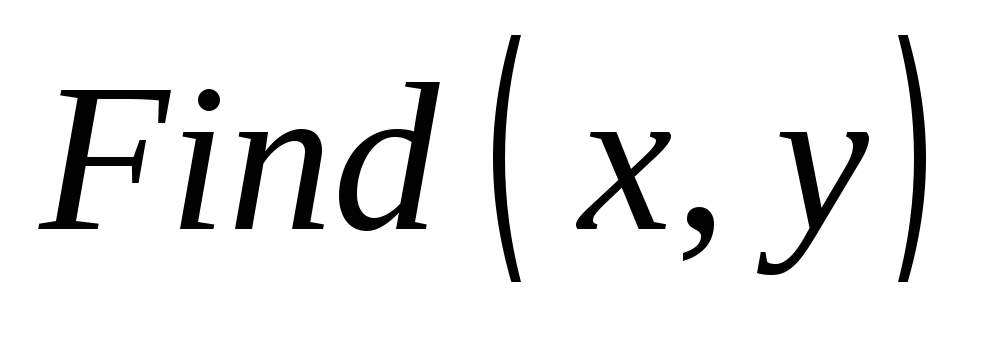. Аргументами функции являются переменные, относительно которых система решается;

• напечатать символьный знак равенства , для этого используется палитра символов или сочетание клавиш.

• щёлкнуть мышью на функции .

Рис.27. Символьное решение системы линейных уравнений с использованием функции Find

Система Mathcad отображает решение уравнений справа от стрелки в виде вектора результатов. Верхняя формула предназначена для вычисления координаты по оси , нижняя по оси.

На рис.28 показан фрагмент программы по расчету профиля кулачка для синусоидального закона движения толкателя с использованием функций пользователя.

В этом фрагменте использованы следующие имена функций для расчета:

• положения толкателя,

• скорости толкателя,

• ускорения толкателя,

Рис.28. Функции определения параметров кулачкового механизма

• углов давления,

• углов профиля кулачка,

• радиус-вектора кулачка.

В скобках после имени функции указываются параметры, являющиеся входными в функцию.

Далее на рис. 29 показан расчетный блок с именем , с помощью которого вычисляются закон движения толкателя и профиль кулачка. В составе расчетного блокаиспользуется оператор цикла, условный оператори оператор иного выбора, а также функции пользователя, показанные выше на рис. 28.

По результатам расчета в полярной системе координат построен центровой профиль кулачка (рис.30). Команда (полярный график) или нажатие комбинациивыводит на экран монитора шаблон таких графиков. Этот шаблон

имеет форму окружности и содержит места ввода данных. Слева от шаблона указывается имя радиус-вектора профиля кулачка, а снизу углов профиля.

Рис.29. Расчетный блок вычисления параметров кулачкового механизма

Рис.30. Профиль кулачка