Лабораторная работа 5

Динамический анализ машинного агрегата

Для определения закона движения входного звена по заданным силам, действующим на звенья механизма, используется уравнение, называемое уравнением движения механизма, которое может быть представлено в различной форме. Одна из наиболее простых форм получается на основании теоремы об изменении

1

2

3

редуктор

электродвигатель

Рис.17. Схема машинного агрегата

кинетической энергии. В некоторых случаях [2] удобно применять уравнение движения механизма, представленное в форме дифференциального уравнения второго порядка. В этой лабораторной работе необходимо разработать программу решения уравнения движения машинного агрегата (рис.17), в котором кривошипно-ползунный механизм приводится в движение от трехфазного, асинхронного электродвигателя переменного тока с короткозамкнутым ротором. Между электродвигателем и кривошипно-ползунным механизмом установлен редуктор. Механическая характеристика электродвигателя

^{где коэффициент скольжения ротора электродвигателя},

максимальный (критический) движущий момент, синхронная угловая скорость ротора электродвигателя, критический коэффициент скольжения.

Рис.18. График механической характеристики

асинхронного электродвигателя

График движущего момента в зависимости от угловой скорости ротора электродвигателя показан на рис. 18.

В дифференциальной форме уравнение движения имеет вид

_,

где дифференциал кинетической энергии;дифференциал работы.

Кинетическая энергия звена приведения

₍₂₅₎

угловая скорость звена приведения,

приведенный момент инерции машинного агрегата

где и массы звеньев,, ,- моменты инерции звеньев механизма и ротора электродвигателя. График зависимости приведенного момента инерции от угла поворота кривошипа показан на рис.19

Д

Рис.19. График приведенного момента инерции машинного агрегата

ифференциал работы

_{. (26)}

после преобразований получим нелинейное дифференциальное уравнение движения машинного агрегата

₍₂₇₎

где

приведенный момент движущих сил,

приведенный момент сил сопротивления (рис.20), сила сопротивления, действующая на участке рабочего хода ползуна.

Рис.20. График приведенного момента сил

Угловое ускорение кривошипа определяется по формуле

.

Для решения уравнения (27) численным методом запишем его в следующем виде

(28 )

Производная от приведенного момента инерции машинного агрегата по углу поворота звена приведения определяется численным методом. Для вычисления производной Mathcad Pro использует модифицированный метод Риддера. Согласно этому методу шаг дифференцирования подбирается таким, чтобы была обеспечена сходимость вычислительного процесса. Поэтому возникает необходимость в интерполяции функции приведенного момента инерции , полученной расчетным путем в отдельных узловых точках. Для этого можно воспользоваться функциями и. Соответствующий фрагмент программы показан на рис.21.

Рис.21. Сплайновая интерполяция функции и определение ее производной cиспользованием функцийcsplineиinterp

Функция вычисляет векторкоэффициентов кубического сплайна с параболическим приближением в конечных точках. Функциявычисляет значения функциис использованием кубических сплайнов для произвольного значения аргументапо предварительно определенному вектору. Необходимо также выполнить интерполяцию функции приведенного момента сопротивления, что требуется для последующего выбора шага при решении уравнения движения машинного агрегата методом Рунге-Кутта четвертого порядка.

В систему Mathcad Pro [1] введена функция . Эта функция используется для решения дифференциального уравнения методом Рунге-Кутта четвертого порядка (рис.22). В скобках после имени функции указываются:

• вектор начальных условий размерности , гдепорядок дифференциального уравнения или число уравнений в системе (если решается система уравнений), а для дифференциального уравнения первого порядка, как в нашем случае, вектор начальных значений вырождается в одну точку;

• граничные точки интервала, на котором проводится поиск решения дифференциальных уравнений;

• число точек (не считая начальной точки), в которых определяется приближенное решение, с его помощью определяется число строк 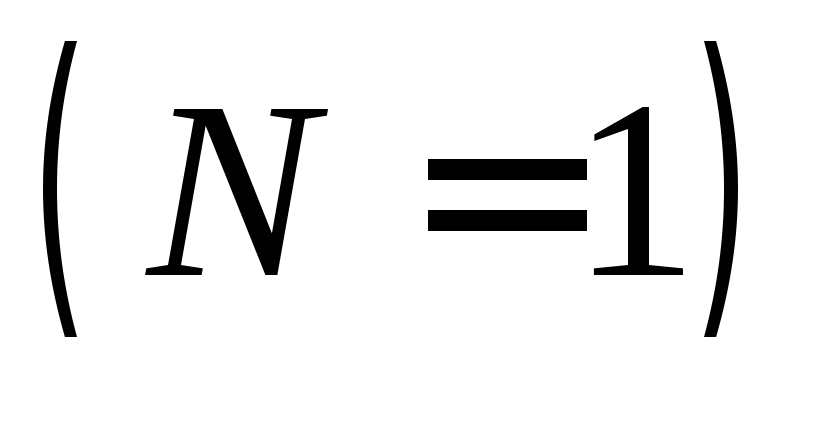в матрице, возвращаемой функцией .

• функция, возвращающая значение в виде вектора из элементов, содержащих первые производные неизвестных функций.

В результате решения получается матрица, имеющая два следующих столбца:

• первый столбец содержит точки, в которых ищется решение дифференциального уравнения;

• второй столбец содержит значения найденного решения в соответствующих точках, то-есть значения угловой скорости звена приведения.

Перед решением дифференциального уравнения движения (27) необходимо задавать начальные условия. При решении уравнения на стадии разгона начальные условия

.

На стадии установившегося движения угловая скорость звена приведения в начале цикла неизвестно и её в первом приближении можно принять равной номинальному значению

Если приведенный момент инерции механизма является величиной постоянной, как, например, в зубчатых механизмах, то дифференциальное уравнение движения имеет вид

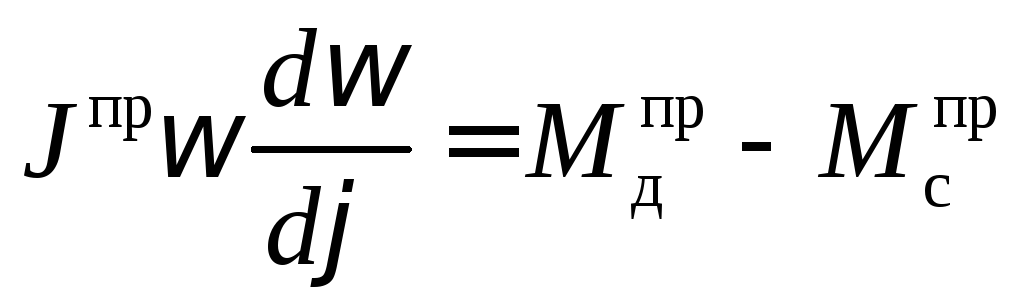(29)

Рис.22. Решение дифференциального уравнения движения машинного агрегата с

использованием функции rkfixed

В результате решения дифференциального уравнения (27) на стадии установившегося движения получаем угловую скорость (рис.23) звена приведения (кривошипа 1) в функции угла поворота .

Угловое ускорение кривошипа (рис.24) в функции угла поворота определяется по формуле

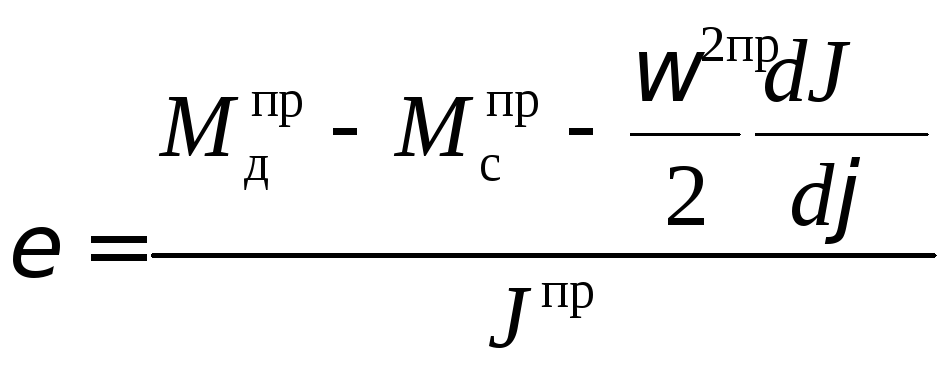(30)

Рис.23 График угловой скорости кривошипа

Для определения времени движения звена приведения в зависимости от угла поворотавоспользуемся выражением

. (31)

Приближенное вычисление определенного интеграла Mathcad выполняет с помощью алгоритма численного интегрирования Ромберга.

Рис.24 График углового ускорения кривошипа