56

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕКСТИЛЬНЫЙ

УНИВЕРСИТЕТ имени А.Н. КОСЫГИНА»

Учебно-методический комплекс

по специальности 150406

“Машины и агрегаты текстильной

и легкой промышленности”

Методические указания

к выполнению лабораторных работ по дисциплине

“ОСНОВЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ”

Составитель проф. С.В. Лушников

МОСКВА 2009

УДК 621.0:004.42(075)

Лушников С.В. Методические указания к выполнению лабораторных работ по дисциплине « Основы автоматизированного проектирования».­­­­­ – М.: ГОУВПО “МГТУ им. А.Н. Косыгина”, 2009. – 51с.

Методические указания посвящены решению задач синтеза и анализа рычажных и кулачковых механизмов, а также исследованию их движения с использованием программной системы компьютерной математики Mathcad. Рассматриваются методы решения указанных выше задач, приемы программирования при организации циклов, решения систем линейных и нелинейных уравнений, дифференциальных уравнений и оптимизационных процедур. Методические указания содержат примеры использования программных блоков для решения типовых математических задач при синтезе и анализе механизмов.

Методические указания предназначены для студентов факультета машиноведения и управления качеством.

Илл. 34, список литературы – 2 наим.

Рецензенты: зав. лабораторией теории механизмов и структуры машин Института машиноведения РАН, профессор, д.т.н. В.А. Глазунов;

профессор кафедры проектирования текстильных машин, д.т. н. В.И. Терентьев.

Подготовлено к печати на кафедре теории механизмов приборов и машин

Содержание Лабораторная работа 1. Синтез кривошипно-ползунного механизма по коэффициенту отношения средних скоростей прямого и обратного хода ползуна…………….4

Лабораторная работа 2. Кинематический анализ кривошипно-ползунного механизма….…………………………………………………………………………......……….10

Лабораторная работа 3.Синтез кривошипно-ползунного механизма методами интерполирования и квадратического приближения.…………………………………...14

Лабораторная работа 4.Синтез кривошипно-ползунного, прямолинейно-направляющего механизма методом оптимизации…………………………………....21

Лабораторная работа 5.Динамический анализ машинного агрегата ….....………....26

Лабораторная работа 6.Синтез и анализ кулачкового механизма......………………34

Лабораторная работа 7.Силовой анализ кривошипно-ползунного механизма.........40

Лабораторная работа 8.Исследование движения упругого толкателя в кулачковом механизме………………………………………………………………………………...45

Список литературы ...........................................................................................................51

Лабораторная работа 1

Синтез кривошипно-ползунного механизма по коэффициенту

отношения средних скоростей прямого и обратного хода ползуна

Синтез кривошипно-ползунного механизма (рис.1,а) по двум крайним положениям выходного звена 3(ползуна) при условии, что входное звено1 является кривошипом, часто встречается в практике проектирования механизмов. Если центр вращения кривошипа1 расположен на линии, проходящей через точки и, определяющие крайние положения ползуна3, линии исовпадают, а механизм называется аксиальным. Коэффициент изменения средней скорости прямого и обратного хода ползуна у такого механизма _.

У дезаксиального

механизма центр вращения кривошипа1 смещен относительно линии на

величину эксцентриситета и этот коэффициент .

Коэффициент отношения средних скоростей обратного и прямого хода ползуна определяется по формуле

₍₁₎

^{где средняя скорость движения ползуна на стадии прямого хода,} _{средняя скорость движения ползуна на стадии обратного хода.}

_{Из формулы (1) следует, что}

₍₂₎

Синтез механизма с использованием системы линейных уравнений

Исходными параметрами для синтеза кривошипно-ползунного механизма являются: ход ползуна , коэффициент соотношения средних скоростей обратного и прямого хода ползуна и угол давления в крайнем правом положении ползуна. Расчет выполняется в прямоугольной системе координат , центр которой (точка₎ делит отрезок на две равные части. Уравнения прямых линий (рис.1,б), проходящих через точки и ^,

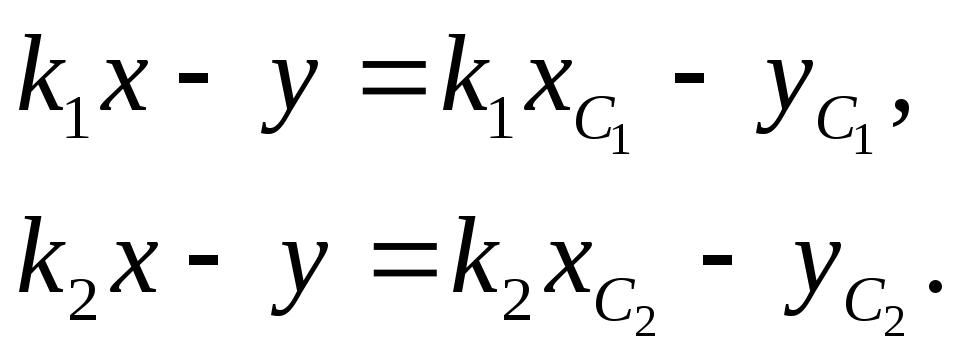₍₃₎

Расчетные формулы для определения коэффициентов системы линейных уравнений (3) имеют следующий вид:

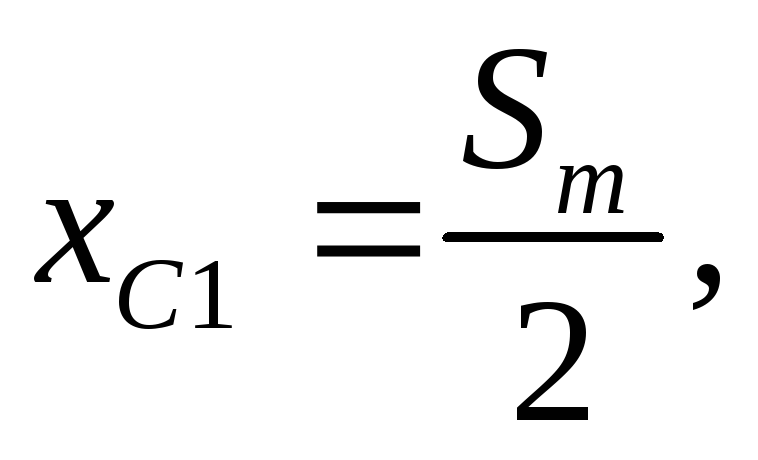
₍₄₎

где иугловые коэффициенты уравнения прямых линий, проходящих соответственно через точкии.

В результате решения системы уравнений (3) получаем координаты точки . Длина кривошипа и длина шатуна определяются по формулам

(5)

Эксцентриситет

Для решения систем линейных уравнений (3) в Mathcad введена функция , которая определяет вектордля системы линейных уравненийпри заданной матрице коэффициентови векторе свободных членов _[1].

Рис.2. Решение системы линейных уравнений cиспользованием функцииlsolve

На рис.2 приведён фрагмент программы синтеза кривошипно-ползунного механизма по заданному коэффициенту производительности, в котором система двух линейных уравнений решается с помощью функции . В первой строчке программы вычисляются значения угла,где означает знак присвоения. Матрицы системы линейных уравнений записываются с помощью палитры знаков.

Синтез механизма с использованием нелинейных уравнений

Для вывода уравнений рассмотрим (рис.1,б), из которого следует

, (6)

^{где ход ползуна , угол и один из размеров, например , являются известными} параметрами. Определяется длина шатуна и эксцентриситет. Уравнение (6) является нелинейным уравнением, заданным в неявном виде, которое может быть решено численными методами. Приступая к решению уравнения, необходимо задать начальное значение искомого параметра . Решение нелинейного уравнения в системеMathcad [1] можно осуществить с помощью функции . На рис. 3,а показан фрагмент программы для синтеза кривошипно-ползунного механизма с решением одного нелинейного уравнения. В скобках функциизаписывается имя

решаемого уравнения и символ того параметра, который определяется.

Рис. 3,а. Решение нелинейного уравнения с использованием

функции root

Эксцентриситет вычисляем по формулам

(7)

_{Система Mathcad позволяет проводить символьные преобразования, в частности из уравнения (6) можно получить выражение в явном виде для определения} ^{длины шатуна . Для этого необходимо выделить курсором переменную (рис.3,б), относительно которой решается уравнение, щелкнуть мышкой по опции} и далее в падающем меню указать на опции

рис.3,б. Решение нелинейного уравнения с использованием символьных преобразований

Если необходимо выполнить синтез механизма по трем параметрам , решаем систему (8) нелинейных уравнений вместе с неравенством, которое ограничивает размер кривошипа.

(8)

В этом случае исходными параметрами являются ход ползуна и угол, а также, расстояние между центром вращения кривошипаи крайним левым положением ползуна. Для решения системы (8) нелинейных уравнений используем функцию. Фрагмент программы с использованием этой функции показан на рис. 4. Для решения системы уравнений необходимо выполнить следующее:

Рис. 4 Решение системы трех нелинейных уравнений с использованием функции Find

• задать начальные приближения для всех неизвестных параметров, входящих в систему уравнений;

• напечатать ключевое слово , которое указывает, что далее следует система уравнений;

• ввести уравнения и неравенства, в которых используются логические знаки, в том числе и знак символического (логического) равенства;

• ввести функцию 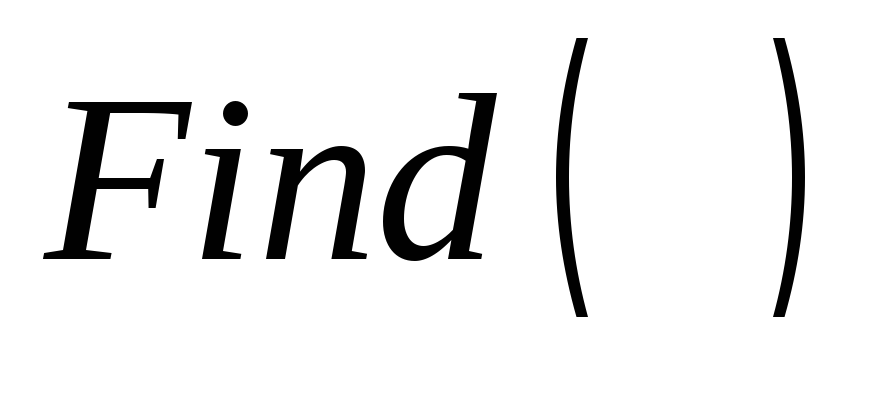, в скобках которой указываются параметры, определяемые при решении системы уравнений;

• результат решения системы присвоен столбцевой матрице .

Mathcad решает уравнения с помощью итерационных методов. На основе начального приближения строится последовательность, сходящаяся к искомому решению. При решении системы нелинейных уравнений Mathcad применяет итерационный метод Левенберга-Маркардта. Если результаты расчета требуется записать в файл данных – файлы ASCII, содержащие числовые данные, можно использовать функцию . В скобках указывается имя файла, в который записываются числовые значения. Каждая строка матрицыстановится строкой в файле.

Для считывания структурированного файла данных применяем функцию . Записывается следующим образом

.

Результат считывания передаётся матрице .