
Проектирование СВЧ-устройств (РТФ 6 семестр Анисимов) / КР / Курсовая работа / Порядок расчета фильтра СВЧ в микрополосковом исполнении
.pdf
Расчет фильтра СВЧ в микрополосковом исполнении
Порядок расчета фильтра нижних частот (ФНЧ) с непосредственными связями между элементами
Эскиз токонесущей части 7-элементного микрополоскового ФНЧ.
Частотная характеристика ФНЧ с потерями.
Исходные данные:
частота среза  ; волновое сопротивления линии передачи
; волновое сопротивления линии передачи  ; отношение толщины полоски к толщине подложки
; отношение толщины полоски к толщине подложки  ; диэлектрическая проницаемость подложки
; диэлектрическая проницаемость подложки  ; потери в подложке
; потери в подложке  ; максимальное
; максимальное
затухание в полосе пропускания  ; вид характеристики; затухание на частоте
; вид характеристики; затухание на частоте 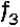 ; заданное затухание
; заданное затухание  . Электрический расчет.
. Электрический расчет.
1.Находим отношение  — нормированную частоту:
— нормированную частоту:  .
.
2.Находим число элементов фильтра  .
.
Для чебышевской характеристики: по графику (рис. 3.9) для  и
и  при
при  .
.
Тот же результат можно получить по формуле  (3.10)
(3.10)

Рис. 3.9. К расчету числа резонаторов фильтра с чебышевской характеристикой затухания.
Для максимально плоской характеристики:  .
.
3. По табл. 3.1 находим для  ;
;  нормированные проводимости элементов
нормированные проводимости элементов  . Для чебышевской характеристики можно воспользоваться таблицей 3.1.
. Для чебышевской характеристики можно воспользоваться таблицей 3.1.
Таблица 3.1
Или по формулам:
- для чебышевской характеристики
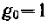 ,
,  ,
,  ;
;

 ;
;  ;
; 
 , (3.4) i= 1, 2, 3,..., п;
, (3.4) i= 1, 2, 3,..., п;
где 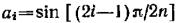 ,
,  , i = l, 2, 3,..., п —1;
, i = l, 2, 3,..., п —1;
- для максимально плоской характеристики при =3 дБ:
, |
, i = 1, 2, 3, ..., п. |
4. Определяем характеристические сопротивления разомкнутых отрезков длиной  =0,1·
=0,1· , аппроксимирующих емкости фильтра-прототипа, учитывая, что
, аппроксимирующих емкости фильтра-прототипа, учитывая, что  , и используя формулу
, и используя формулу
 (3.7):
(3.7):

5. Определяем характеристические сопротивления короткозамкнутых отрезков длиной 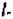 =0,1·
=0,1· , аппроксимирующих индуктивности фильтра-прототипа
, аппроксимирующих индуктивности фильтра-прототипа
(3.6):
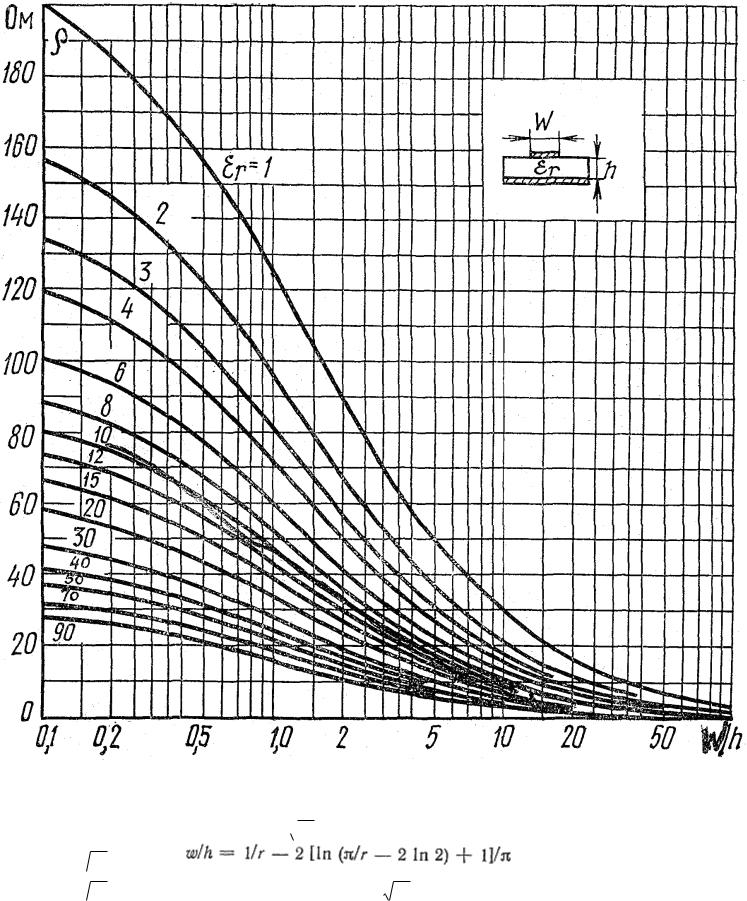
По данным электрического расчета определяем конструктивные размеры элементов фильтра, используя формулу  (3.8) и графики рис. 3.6; 3.10.
(3.8) и графики рис. 3.6; 3.10.
Рис. 3.6. Зависимость характеристического сопротивления несимметричного колоскового волновода от его геометрии.
Рис. 3.10. Эквивалентная диэлектрическая проницаемость несимметричного полоскового волновода.
Вольман:
Размеры несимметричной полосковой линии по заданному ZВ определяются по формулам, имеющим
максимальную погрешность 0,6% при Z B 
 r 132 Ом
r 132 Ом
-при
-при
Z Z
B 
B 
r
r
120 Ом
120 Ом
 , где
, где
r Z |
B |
|
r |
|
|
 (120 )
(120 )
.
,
По Ковалеву:
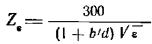 - для несимметричных полосковых волноводов;
- для несимметричных полосковых волноводов;
Ширина оконечных  -омных полосок находится по графику рис. 3.6. Длины
-омных полосок находится по графику рис. 3.6. Длины  -омных отрезков
-омных отрезков  выбираются произвольно.
выбираются произвольно.

6. Определяем активные потери в фильтре на частоте среза для 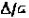 ;
;  . Потери в металле (по графику рис. 3.8)
. Потери в металле (по графику рис. 3.8)
 , где
, где  (для меди).
(для меди).  - поверхностное сопротивление материала полосок (Ом);
- поверхностное сопротивление материала полосок (Ом);
Рис. 3.8. Относительное затухание в несимметричном полосковом волноводе с твердым диэлектриком.
Затухание в диэлектрике  .
.
Потери в фильтре  (3.9)
(3.9)
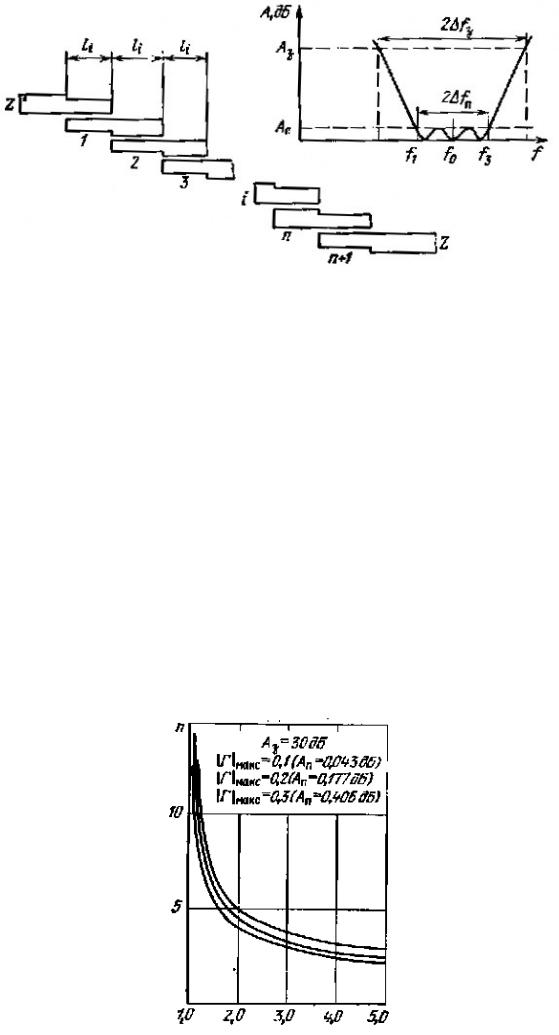
Порядок расчета полосового фильтра с электромагнитными связями между элементами
Структурная схема фильтра на связанных полуволновых резонаторах и его частотная характеристика. Исходные данные:
средняя частота полосы пропускания  ; на границах полосы заграждения
; на границах полосы заграждения  затухание равно
затухание равно  , характеристика чебышевская (максимально плоская), максимальное затухание в полосе пропускания
, характеристика чебышевская (максимально плоская), максимальное затухание в полосе пропускания  ; полоса пропускания
; полоса пропускания  , высота подложки
, высота подложки  ; отношение толщины проводника к высоте подложки
; отношение толщины проводника к высоте подложки  ;
;
диэлектрическая проницаемость подложки 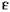 ; потери в подложке
; потери в подложке 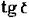 0. Электрический расчет.
0. Электрический расчет.
l. Определяем отношение  =3,1.
=3,1.
2. Число полуволновых резонаторов  определяется по следующим формулам:
определяется по следующим формулам:
-для максимально плоской характеристики  ; (3.11а)
; (3.11а)
-для чебышевской характеристики  . (3.11б)
. (3.11б)
Или по графику рис. 3.13 определяем 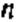 для
для  ,
,  ;
;  .
.
Рис. 3.13. Графики для определения числа резонаторов полосового фильтра с чебышевской характеристикой

3. Находим значения элементов |
(табл. 3.4) для относительной полосы прототипа |
с |
чебышевской характеристикой |
|
|
|
|
Таблица 3.4 |
4. Определяем величину переходных затуханий (дБ) связанных звеньев:  .
.
По данным электрического расчета определяем конструктивные размеры элементов фильтра, используя таблицу (3.5), графики рис. 3.6, 3.10 и формулы (3.12), (3.13).
Таблица 3.5

Рис. 3.6. Зависимость характеристического сопротивления несимметричного колоскового волновода от его геометрии.
Рис. 3.10. Эквивалентная диэлектрическая проницаемость несимметричного полоскового волновода.
Длина резонатора  , (3.13)
, (3.13)
где  (3.12) - концевая емкость каждого резонатора (Ф).
(3.12) - концевая емкость каждого резонатора (Ф).
5. Ширина оконечных  -омных полосок находится по графику рис. 3.6.
-омных полосок находится по графику рис. 3.6.
Длины  -омных отрезков
-омных отрезков  выбираются произвольно. Теперь все размеры фильтра определены.
выбираются произвольно. Теперь все размеры фильтра определены.

6. Величину активных потерь в фильтре на средней частоте полосы пропускания можно определить по формуле
Вэту формулу входят значения элементов  фильтра-прототипа нижних частот, которые берем из табл.
фильтра-прототипа нижних частот, которые берем из табл.
3.1(с чебышевской характеристикой) для  и
и  . Их можно рассчитать по формулам.
. Их можно рассчитать по формулам.
Таблица 3.1
Величину |
(ненагруженную добротность центрального резонатора) определим как |
. (3.15) |
|
|||
Значение |
берем |
из |
графика рис. 3.14, а множитель |
находим по формуле |
(3.16) для |
; |
=1/( |
)2; ; |
( |
). |
|
|
|
Рис. 3.14. Графики для определения добротности полосового фильтра.
