33. Уравнение электродиффузии Нернста-Планка.

Вклад электрического поля в диффузию описывает уравнение электродиффузии Нернста-Планка, которое характеризует процесс пассивного транспорта ионов в поле электрохимического потенциала. Поток J заряженных ионов пропорционален градиенту электрохимического потенциала в направлении оси x и зависит от подвижности и концентрации ионов:

, где

F - число Фарадея,

z - валентность иона,

T - абсолютная температура,

R - газовая постоянная, 

φ - электрический потенциал на мембране.

х задает положение точки в толще мембраны х = 0 внутренняя сторона мембраны (i), х = L — наружная сторона мембраны (o), т.е. L – толщина мембраны.

Из условия J = 0 получим уравнение Нернста

  .

Разделив на D и c, после интегрирования , или в стандартном виде:

, где

V_s – разность потенциалов   на мембране

34. Потенциал покоя. Уравнение Гольдмана -Ходжкина -Каца.

Основные предположения:

- внутримембранное поле постоянно:

- примембранные концентрации ионов равны их концентрациям в глубине раствора;

- не учитываются локальные отличия в плотности заряда в мембране в результате движения зарядов.

Тогда уравнение Нернста-Планка приобретает следующий вид:

 где

V –разность потенциалов,

L – толщина мембраны.

Из этого уравнения получаем следующее уравнение:

Решение которого для с после преобразований даст уравнение:

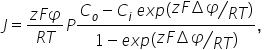где

УРАВНЕНИЕ ГОЛЬДМАНА

J – поток иона, моль/см² * сек, которое описывает пассивный поток иона через мембрану, P – коэффициент проницаемости (D/L) мембраны для иона.

Уравнение Гольдмана предсказывает нелинейную зависимость трансмембранного потока ионов от разности потенциалов на мембране.

После преобразований можно получить формулу для V_r (разности потенциалов, ЭДС - электродвижущей силы) для случая трех основных ионов Na⁺, K⁺ и Cl^-, участвующих в создании  мембранного потенциала:

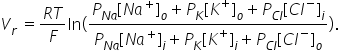
ТО САМОЕ УРАВНЕНИЕ ЗАПЛУПОЦКОГО И ХУЕБЛЯТСКОГО ТАМ ЕЩЕ ЧЕ ТО

Соотношение проницаемостей для ионов Na⁺, K⁺ и Cl^- составляет Р_к :P_Na:Р_Cl = 1:0.04:0.05

Уравнение Гольдмана-Ходжкина-Каца позволяет рассчитывать разность потенциалов` в состоянии покоя и в состоянии возбуждения. ЭДС в состоянии покоя называют потенциалом покоя (ПП), в состоянии возбуждения - потенциалом действия (ПД). Численное значение потенциала покоя (ПП) можно рассчитывать по формуле:

.

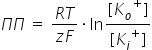Разница между проницаемостями К+ и Na+ определяет только направление катионного потока, который создает ПП на БМ.

35. Модель мембраны как электрической цепи. Основное уравнение для электрофизиологических моделей.

Мембрана разделяет заряды, то есть является конденсатором, обладающим электроемкостью, что можно выразить через следующую формулу:

 где

С_m – электроемкость мембраны; S — площадь обкладки конденсатора (площадь поверхности клетки); d — расстояние между обкладками (толщина мембраны); ε — относительная диэлектрическая проницаемость; Q — заряд на обкладке; V = Vi - Vo — разность потенциалов внутри и снаружи клетки.

Мембрана может быть представлена в виде электрической цепи.

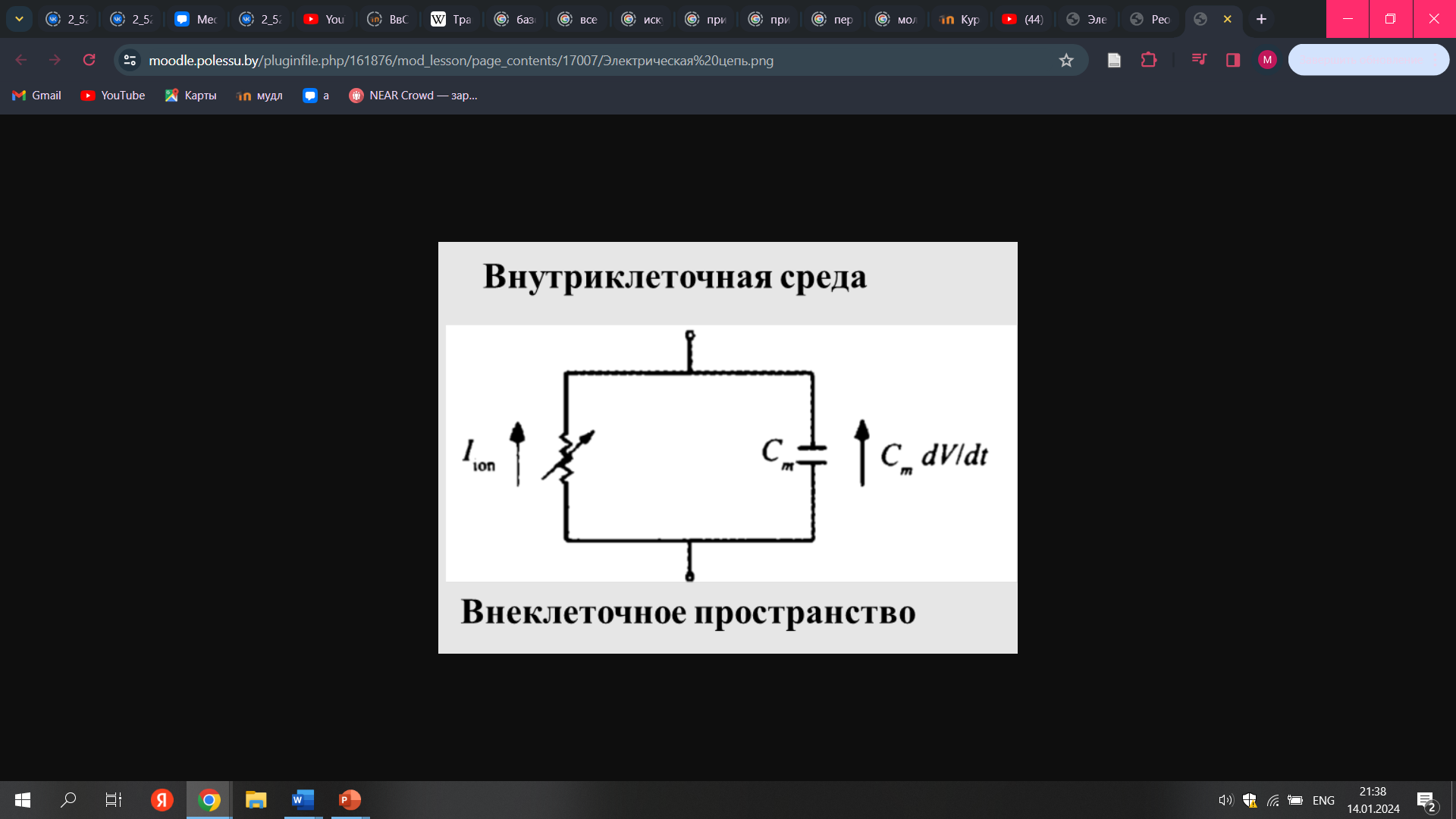
Поскольку нет накопления заряда на каждой из сторон мембраны сумма ионного и емкостного тока должна быть равна нулю.

 Отсюда можем получить уравнение для электрофизиологических моделей, отражающего зависимость динамики мембранного потенциала от ионного тока через мембрану: