makry_zachet

Сверхпроводимость с микроскопической точки зрения:

В Ме имеются электроны и фононы, кванто-упругие колебания решетки.

Из-за электрон-фононного взаимодействия возможно образование так называемых куперовских пар. Связанных состояний пар электронов, которые являются основой для теории сверхпроводимости, поэтому микроскопической точки зрения Возникают такие пары, которые являются бозонами, поскольку два электрона спариваются. В системе бозона возможно явление сверхтекучести. Сверхтекучесть куперовских пар и есть сверхпроводимость. Для того, чтобы возникала серхтекучесть необходимо, чтобы спектр возбуждения в системе удовлетворял некоторому условию.

Природа сверхтекучести

Рассмотрим спектр возбуждения в Ме который находится в сверхпроводящем состоянии

- щель

Если спектр устроен таким образом, то можно написать условие, при котором возможно возбуждение в такой системе.

Рассмотрим бозонную систему. Если эта система движется со скоростью v, то энергия, соответствующая возбуждению такой системы, определяется таким выражением:

ε (p) + p v

Минимальным это выражение будет, если они направлены в противоположные направления.

ε (p) − pv

Если эта величина меньше 0, то в такой системе могут возникать возбуждения. (понижается энергия)

Вслучае такого спектра выполняется условие:

ε(p) > V , данное соотношение больше некоторой критической скорости. И

p

тогда не выгодно энергетически возникать возбуждению в такой системе. Система течет без возникновения возбуждения.

Поэтому критически для возникновения сверхпроводящего состояния необходимо наличии щели.

Фазовый переход в сверхпроводнике

Напишем выражение для свободной энергии сверхпроводника:

F = F0 + 12 a 2 + 14 b 4

Теперь нам нужно показать что при некоторой критической температуре величина щели обращается в 0, а при некоторой отлична от 0.

Будем предполагать, что а ведет себя в окрестности критических температур след образом:

a = α (T − Tc )

Равновесному состоянию будет отвечать минимум свободной энергии. Продифференцируем это выражение и находим:

a + b 3 = 0

Щель при возбуждении в зависимости от температуры ведет себя соответствующим образом.

Вычислим значение свободной энергии в положение минимума.

Мы получили выражение, когда МП отсутствует, а теперь рассмотрим как изменится ситуация, если мы накладываем на систему МП.

Строго говоря это выражение, чтобы можно было использовать для Ме в нормальном состоянии и в сверхпроводящем, нужно умножить на функцию

f ( ) = {1, T < Tc 0, T > Tc

которая учитывает переход из одного состояния в другое.

К чему приведет возникновение дополнительного слагаемого в свободной энергии?

0 =

Возможна ситуация, когда минимум свободной энергии, локальный минимум при 0, будет по глубине такой же (равен 0), то есть совпадать со значением F при = 0. В этом случае состояние сверхпроводящее перестанет быть выгодным. Значение отличное от нуля обеспечивает нам минимум своб. энергии. При нуле никакого энергетического выигрыша при переходе в сверхпроводящее состояние не произойдет.

Найдем при каком значении МП переход в сверхпроводящее состояние перестает быть выгодным?

F = F0 − α2 (Tc − T)2 + H2

4b 8π

Получаем выражение для своб. энергии. Перестанет быть выгодным, когда две добавки дадут в результате 0.

− α2 (Tc − T)2 + H2 = 0 4b 8π

Из этого соотношения мы предполагаем, что подключаем МП, а наш образец в сверхпроводящем состоянии.

HkP = α (Tc − T)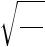

При H<Hкр МП не разрушает сверхпроводящее состояние

Экспериментальная картинка

Hkp Tc2 − T2

Как критическая температура зависит от МП?

Критическая темп-ра зависит от приложенного к сверхпроводнику МП

Если у нас имеется ток который окружен сверхпроводящей оболочкой

H 1r

Возникает критический радиус

r> rkp, H > Hkp (T)

r< rkp, H < Hkp (T)

Магнитный поток через сверхпроводящее кольцо

Сохранение магнитного потока Рассмотрим кольцо, по которому течет ток.

Из-за того, что уравнение линейное, МП будет пропорционально току H I

1

Поэтому магнитный поток можно записать в виде ϕ = с LI

Теперь, если мы помещаем кольцо стоком во внешнее МП, то можно записать соотношение ϕ = ϕ0 + 1c LI

Теперь, если речь идет о сверхпроводящем кольце, то мы можем утверждать, что в этом случае сохраняется магнитный поток. Посмотрим на уравнение Максвелла.

rotE = −1 ∂H c ∂t

Проинтегрируем обе части уравнения по поверхности и воспользуемся теоремой Стокса

∫ d f rotE = d l E = − 1 ∂ϕ C ∂t

Поскольку у нас на поверхности сверхпроводника El S = 0 , то интеграл по поверхности равен 0 и ϕ = const.

Другими словами, если мы меняем внешнее МП, то у нас в сверхпроводящем кольце возникает такой ток, который обеспечивает сохранение магнитного потока. Эту картину можно себе представить след. образом. Если у нас как неизменность количество силовых линий МП, проходящих через сверхпроводящее кольцо. Теперь с законом сохранения потока связан ? возбуждения тока в кольце. Для этого кольцо помещают при температуре T>Tc в МП, потом охлаждают до T<Tc и МП выключают. В результате в сверхпроводящем кольце возбуждается ток, который обеспечивает сохранение магнитного потока.

Магнитный поток через сверхпроводящее кольцо квантуется. Получим соотношение, которое иллюстрирует закон квантования. Рассмотрим правило квантования Бора-Зоммерфельда.

Носителями являются куперовские пары, поэтому получается следующее

(2m v + 2ce A) d l = 2π n

Далее проведем контур внутри кольца. По поверхности нет тока

2ce Ad l = 2π n

Используя теорему Стокса, преобразуем

соотношение определяет условие квантования магнитного потока.

Квазистационарное электромагнитное поле. Основные уравнения и граничные условия. Поглощаемая энергия. Проникновение магнитного поля в проводник (при больших частотах). Скинэффект. Распределение тока в цилиндрическом проводнике.

Квазистационарное ЭМП

Рассмотрим уравнение Максвелла. Мы предполагаем что магнитная проницаемость равна 1, поэтому пишем H. Сторонних зарядов нет.

условие, когда им можно пренебречь. Внутри проводника рассмотрим проводник. Будем считать, что действует закон Ома (считаем, что среда

изотропна): j = σE

Если у нас рассматривается сам проводник, нам нужно сравнить два слагаемых в rot H

Будем предполагать, что поле меняется по гармоническому закону E, H e−iωt

1c σE 1c ε (−iω) E

σ

ω ε Это условие, когда можно пренебречь слагаемым по сравнению с током.

Вне проводника для условия нам нужно сравнить второе слагаемое с rot H,

HL εс (−iω) E, LE2 εc (iωc ) (−iω)E

c

ε = 1, L << ω Размер проводника должен быть много меньше, чем длина

волны излучения ЭМ. Это условие напоминает дипольное приближение. Условие пренебрежения запаздыванием в уравнении Максвелла. В случае выполнения этих двух неравенств получаем ситуацию, называемую квазистационарное ЭМП.

Уравнения, которые отвечают этой ситуации:

Такое же уравнение можно получить для электрического поля. Действуем на первое уравнение:

1 ∂ graddivE − E = − c ∂t rotH

divrotH = 0 = 4cπ σdivE, divE = 0

4π ∂E − E = − c2 σ ∂t

Эти уравнения дополним граничными условиями:

( j ) S = 0, (E) S = 0

n n

(Hin) S = (Hex ) S n n

Также тангенциальная компонента МП должна быть непрерывной.

Рассмотрим вопросы, относящиеся к квазистационарному МП.

Проводник помещен в переменное МП H e−iωt

Под его действием возникают токи в проводнике и в силу закона Ома, эти тока пропорциональны ЭП. Кроме того, закон Ома предлагает такое движение электронов по проводнику, сопровождающееся столкновением с примесями,