makry_zachet

1

2 ∫ [rdl] = S — площадь витка с током, поэтому

M = Ic S

Система линейных токов в ограниченной области пространства. Индуктивность

Имеем замкнутые линейные токи, расположенные в ограниченной области. (Ограниченность нам нужна для того, чтобы использовать тот факт, что на бесконечности от системы поле обращается в ноль.)

Магнитный поток через заданный а-тый виток с током:

Φa = ∫ Bdfa = ∫ rotA dfa = A dla

Laa — индуктивность проводника

Энергетические соотношения для системы токов в вакууме

μ = 1:

зарядов, дви-

движущихся без сопротивления.) вводя векторный потенциал H = rot A,

rot H = 4cπ j

1

W = 2c ∫ dV jA, где интегрирование проводиться по объему проводников

тк вне их j = 0. Предположим что имеем систему линейных токов,тогда будем интегрировать по попереченому сечению проводников.

1

W = 2c ∑a IaФa, можно переписать в виде:

обобщенная сила соотв. магнитному потоку Фа, пропорциональна полному току протекающему в данном контуре.

получим выражения для энергии и работы, в которых в качестве внешних параметров выбраны токи.

наличии диссипации энергии в проводниках. Так же как и в случае электростатики, включает в себя переменную часть энергии источников. Подставляя в предыдущее получим:

δW = − 1c ∫ dV Aδj Объемные токи аналогичны потенциалас в электростатике провожников, а векторный потенциал - зарядам.

ТД соотношения для магнетиков в постоянном магнитном поле

В присутствии магнетиков ранее полученные соотношения видоизменяются, т.к. теперь необходимо различать B и H. Теперь имеем

где U0 — внутренняя энергия магнетика в отсутствие поля.

Внутренняя энергия U является ТД потенциалом по отношении к индукции B. Введём свободную энергию

B2

F(B) = F0 + ∫ dV 8

πμ

HδB δF = −SδT − pδV + ∫ dV 4π

~

U является ТД потенциалом при выборе в качестве внешнего параметра плотности тока j или напряженности H, т.к. j и H однозначно связаны

5. Пироэлектрики. Фазовый переход в сегнетоэлектриках.

Пироэлектрические вещества - это класс веществ, которые и в отсутствие внешнего электрического поля могут обладать отличной от нуля плотность дипольного момента P(cпонтанная поляризация)

Pi = P0i + ϰik Ek

Di = D0i + εik Ek , где D0 = 4πP0

Сформулируем электростатическую задачу об определении напряженности, создаваемая пироэлектриком.

rotE = 0,

divD = 0, причем D и E связаны Die = D0ei + εik Eke вне тела(e) и Di = Ei внутри(i)

Имеем след. граничные условия:

Eti s = Ete s

ni(D0i + εik Ek(i)) s = En(e) s ,отличие от диэлектрика в наличие доп. слагаемого Don s

Ere→∞ → 0

Сведем задачу к задаче об диэлектрике, для этого введем новые поля Ei →

Ei + E

Ee → Ee + E

Тогда граничные условия будут иметь вид:

Eti s = Ete s

ni(D0i − (εik − δik )Ek + εik Ek(i)) s = En(e) s Ere→∞ → E

Задача сведется к задаче о диэлектрике, если ni(D0i − (εik − δik )Ek ) s = 0. Направим оси x,y,z по главным осям тензора εik , тогда

Ei = D0i , где нет суммирования по повторяющимся индексам, а

εii−1

подразумевается главное значение тензора.

Таким образом мы свели к задаче о диэлектрике. Тогда, например, полный дипольный момент считается по формуле:

Например, для шара V 3P0i

εii+2

Свойства

Пироэлектричество означает выстроенность эл-ых дипольных моментов. В газах и жидкостях такое выстраивание требует затраты энергии, следовательно энергетически невыгодно. Следовательно, это свойство обнаруживается при особой закономерности в расположении атомов, т.е. в кристаллах. Однако, требуется еще чтобы при всех преобразованиях симметрии оставалась неизменна ось, по которой направлен вектор P0 . Данному требованию удовлетворяют кристаллы с гексальной и ромбической решетками.

Сегнетоэлектрики - вещества, у которых переход из пироэлектрическую фазу в непироэлектрическую фазу является переход II рода. Пироэлектрическая ось - ось, по которой направлен вектор P0

Точка фазового перехода называется точка Кюри. При достижении температуры Кюри Tc происходит скачкообразное изменение симметрии кристаллической решетки, достигаемое путем максимального смещения отдельных атомов.

Следующие свойства получены из эксперимента.

1. Плотность спонтанного момента P0

P0 (T < T c)

P0 = 0 (T > T c)

2. Компонента тензора диэлектрической восприимчивости, соотв. направлению сагнетоэлектрической оси

Получим теоретическое объяснение, для этого разложим свободную энергию по степеням плотности дипольного момента P0(в интересующей нас области температур последняя мала)

F = F0 + 1/2VaP 2 + 1/4VbP 4 − V P E, где V - объем, а последний член связан с помещением тела во внешнее поле. Заметим, что для того, чтобы существовал минимум необходимо b>0.

1. Изучим разложение в отсутствие внешнего поля, тогда = V P (a +

bP 2) = 0. Имеем два случая, если а>0, то P=0, это непироэлектрическая фаза. Если а<0, то P0 = , т.е. при а=0 достигается температура Кюри и

можно разложить а в ряд, тогда при T<T_c P0 = ±, знаки равносильны, так как энергия одна и та же

Видны два минимума, равные по модулю

термодинамически равновестное знаечние Р_0, которое мы нашли в пред. пункте, тогда

ϰ= (α(T − Tc ))−1 (T > Tc )

ϰ= (2α(Tc − T ))−1 (T < Tc )

Характеристики сигнетоэлектриков вблизи точки фазового перехода.

Свободная энергия в отсутствии магнитного поля имеет зависимость

P0 = ±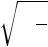, где в окрестности критической точки a = α(T − Tc )

Если мы накладываем электрическое поле, то график пунктирный, возникает два состояние стабильное и метастабильное.

6. Ферромагнетизм. Фазовый переход в ферромагнетике. Энергия магнитной анизотропии, ориентация вектора намагниченности в одноосном кристалле

Ферромагнетики

Рассмотрим вектор магнитной индукции(B)i = (H)i = 4πMi, где M− плотность магнитного момента вещества.

Mi = Mi(0) + χik Hk, Mi(0)−вектор спонтанной намагниченности,

который не связан с приложенным к магнетику внешнем магнитным полем.

Вещества у которых Mi(0) = 0 называются ферромагнетиками.

Имеется фазовый переход при критической температуре Tc

Происхождение ферромагнетизма:

Ферромагнитизм обусловлен обменным взаимодействием (обменное взаимодействие связано с ориентацией спинов, или с симметрией ВФ электронов) и выигрыш за счет обменного взаимодействия позволяет спонтанной намагниченности быть отличной от нуля. Этот эффект оказывается намного более сильным чем взаимодействие магнитных моментов электронов и поэтому в первом приближении мы не рассм. взаим связанное с ориентацией магнитных моментов. Появление спонтанной намагниченности не связано с кристаллической решеткой вещества в котором происходит ферромагнитный переход, поэтому вектор спонтанной намагниченности в данном случае может быть повернут куда угодно относительно крист. решетки.

Рассмотрим свободную энергию и разложим ее в окр -ти Tc:

предположим, что a = α(T − Tc ) в окрестности Tc . Чтобы найти значение положения минимума F, M и связь M с H, продифференцируем F по М. Энергетически выгодна ситуация, когда M H (MH) = MH

∂F = aM + bM3 − H = 0 ∂M

Если H = 0 M0 = = , T < Tc или M0 = 0, T >

Tc

Найдем восприимчивость χ, дифференцируя по Н

В самой критической точке восприимчивость обращается в бесконечность.

Такая теория позволяет пописать поведение магнитной восприимчивости и намагниченности в окрестности критической точки.

Энергия магнитной анизотропии

(Ориентация спонтанной намагниченности если T < Tc )

M = M0 + χH если мы далеко от Tc ,и там вектор M0 χH, тогда χH можно принибречь ( в самой критической точке M(0) )

Т.о. T < Tc , M = M0

Тк полученные выше значение не зависят от ориентации, рассмотрим доп. слагаемые которые влияют на значение свободной энергии F и приводят к зависимости F от ориентации M. Эти слагаемые возникают за счет взаимодействия магнитных моментов электронов и зависят от кристал. структуры в - ва

Для одноосного кристалла βxx = βyy =

β , βzz = β

βik = β (Mx2 + My2) + β Mz2 = = (β M2 cos2 θ + β M2 sin2 θ)

F = 12 (β M2 cos2 θ + β M2 sin2 θ) − MH

Рассм. случай когда имеется ось легкого намагничивания т.е. β < β

F = 12 (β M2 cos2 θ + β M2 sin2 θ − β M2 sin2 θ + β M2 sin2 θ) −

MH = 12 (β M2 + (β − β )M2sin2θ) − MH

β M2− не зависит от ориентации, не будем его учитывать

F = 12 (β − β )M2sin2θ − MH

cos ϑ = cos θ cos θH + sin θ sin θH (cos(φ − φH )

φ, φH −азимутальные углы

последнее слагаемое не влияет не будем его учитывать

H

Видно, что min при sin θm = M(β − β ) тк 0 ≤ θ ≤ π имеем 2 угла:

θm, π − θm