Раздел 2. Расчёт сечения крыла.
По заданию расчётным является сечение 2-2.
В этом сечении
,
хорда сечения
.
2.1. Определение нормальных напряжений.
Для расчёта сечения крыла на нормальные напряжения воспользуемся методом редукционных коэффициентов. Данный метод учитывает возможную потерю устойчивости и превышение предела текучести материала в отдельных силовых элементах.
В процессе расчёта методом редукционных коэффициентов материал всех элементов приводится к одному, называемому «фиктивным», отличительной особенностью которого является сохранение линейной зависимости между деформациями и напряжениями вплоть до разрушения.
Критические напряжения общей потери устойчивости стрингеров определяется по формуле Эйлера:
где
– расстояние между нервюрами;
- коэффициент закрепления по краям;
- радиус инерции силового элемента.
Критические напряжения обшивки и местной
потери устойчивости полок силовых
элементов вычисляются при
:
где
- коэффициент закрепления,
- ширина полки,
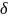- толщина полки.
Для лонжеронов -
;
Для стрингеров -
;
Для обшивки -
.
Отмечаем на диаграмме
-
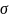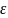стали и дюраля участок сжатой зоны и
обрываем по получившимся значениям.
Диаграмма растяжения/сжатия материалов.
2.1.1. Построение расчётной модели сечения крыла.
Заданное сечение крыла заменяется моделью, состоящей из продольных силовых элементов с присоединённой к их площади обшивкой. Получаем приведённые площади силовых элементов и их координаты.
Величина приведённой площади силовых элементов определяется с помощью гипотезы Кармана, т.е.:
где
- площадь сечения i-го
силового элемента;
- шаг силовых элементов;
- толщина обшивки;
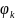- редукционный коэффициент Кармана:
Расчёты приведены в таблице.
Элемент |
Номер |
X, мм |
f эл [мм^2] |
b0 [мм] |
дельта [мм] |
Фи k |
f пр i [мм^2] |
Пояс лонжерона |
1 |
600 |
1250 |
75 |
2,5 |
0,0913 |
1 267,12 |
Стрингер |
2 |
750 |
160,9 |
150 |
2,5 |
0,5071 |
351,06 |
Стрингер |
3 |
900 |
160,9 |
150 |
2,5 |
0,5071 |
351,06 |
Стрингер |
4 |
1050 |
160,9 |
150 |
2,5 |
0,5071 |
351,06 |
Стрингер |
5 |
1200 |
160,9 |
150 |
2,5 |
0,5071 |
351,06 |
Стрингер |
6 |
1350 |
160,9 |
150 |
2,5 |
0,5071 |
351,06 |
Стрингер |
7 |
1500 |
160,9 |
150 |
2,5 |
0,5071 |
351,06 |
Стрингер |
8 |
1650 |
160,9 |
150 |
2,5 |
0,5071 |
351,06 |
Стрингер |
9 |
1800 |
160,9 |
150 |
2,5 |
0,5071 |
351,06 |
Стрингер |
10 |
1950 |
160,9 |
150 |
2,5 |
0,5071 |
351,06 |
Стрингер |
11 |
2100 |
160,9 |
150 |
2,5 |
0,5071 |
351,06 |
Пояс стенки |
12 |
2250 |
110,1 |
75 |
2,5 |
0,5071 |
205,18 |
Пояс стенки |
13 |
2250 |
110,1 |
103,125 |
2,5 |
1,0000 |
367,91 |
Стрингер |
14 |
2043,75 |
160,9 |
206,25 |
2,5 |
1,0000 |
676,53 |
Стрингер |
15 |
1837,5 |
160,9 |
206,25 |
2,5 |
1,0000 |
676,53 |
Стрингер |
16 |
1631,25 |
160,9 |
206,25 |
2,5 |
1,0000 |
676,53 |
Стрингер |
17 |
1425 |
160,9 |
206,25 |
2,5 |
1,0000 |
676,53 |
Стрингер |
18 |
1218,75 |
160,9 |
206,25 |
2,5 |
1,0000 |
676,53 |
Стрингер |
19 |
1012,5 |
160,9 |
206,25 |
2,5 |
1,0000 |
676,53 |
Стрингер |
20 |
806,25 |
160,9 |
206,25 |
2,5 |
1,0000 |
676,53 |
Пояс лонжерона |
21 |
600 |
1250 |
103,125 |
2,5 |
0,3333 |
1 335,94 |
Построение расчётной модели крыла.
По имеющимся значениям площадей и координат всех силовых элементов определяется положение центра масс приведённого сечения.
Координата по оси ОХ ЦМ сечения:
Координата по оси ОY ЦМ сечения:
Момент инерции сечения относительно оси ОХ:
Момент инерции сечения относительно оси ОУ:
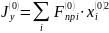
Центробежный момент инерции сечения крыла:
Приведённый момент инерции сечения относительно оси ОХ:
Приведённый момент инерции сечения относительно оси ОУ:
Приведённый центробежный момент инерции сечения крыла:
После этого определяются фиктивные напряжения в каждом силовом элементе сечения в нулевом приближении:
где
- коэффициент асимметрии профиля:
Получим истинное напряжение в нём в нулевом приближении.
Отношение истинного напряжения в данном элементе к фиктивному даёт редукционный коэффициент первого приближения. В нашем случае напряжения в силовых элементах не превысили предела текучести.
Выполним после нулевой итерации ещё первую.
Все расчёты произведены в таблицах.
По результатам расчёта первой итерации построена эпюра нормальных напряжений в сечении крыла.
Элемент |
Xi |
Yi |
F пр. i, (0) |
F*x |
F*y |
F*x^2 |
F*y^2 |
F*x*y |
yi - Y0 |
xi - X0 |
Сигма i фикт. (0) |
Сигма i ист. (0) |
Ф (1) |
1 |
600 |
469,9 |
1 267,12 |
760270 |
595431 |
456161879 |
279799194 |
357258626 |
265,3 |
-678 |
25,66787866 |
25,66787866 |
1 |
2 |
750 |
486,3 |
351,06 |
263295 |
170731 |
197471085 |
83031640 |
128048225 |
281,7 |
-528 |
27,9975077 |
9,127187512 |
0,326 |
3 |
900 |
494,0 |
351,06 |
315954 |
173414 |
284358363 |
85662168 |
156072912 |
289,4 |
-378 |
29,3914048 |
9,581597963 |
0,326 |
4 |
1050 |
494,6 |
351,06 |
368613 |
173643 |
387043327 |
85887895 |
182324811 |
290,0 |
-228 |
30,03967959 |
9,792935546 |
0,326 |
5 |
1200 |
489,5 |
351,06 |
421272 |
171859 |
505525979 |
84132697 |
206231094 |
284,9 |
-78,4 |
30,0769625 |
9,805089776 |
0,326 |
6 |
1350 |
479,7 |
351,06 |
473931 |
168397 |
639806317 |
80776825 |
227335705 |
275,1 |
71,62 |
29,60431859 |
9,65100786 |
0,326 |
7 |
1500 |
465,8 |
351,06 |
526590 |
163514 |
789884341 |
76160627 |
245271455 |
261,2 |
221,6 |
28,7003798 |
9,356323814 |
0,326 |
8 |
1650 |
448,4 |
351,06 |
579249 |
157417 |
955760053 |
70586746 |
259738315 |
243,8 |
371,6 |
27,42754687 |
8,941380281 |
0,326 |
9 |
1800 |
428,0 |
351,06 |
631907 |
150270 |
1137433452 |
64322261 |
270485288 |
223,4 |
521,6 |
25,83569298 |
8,422435911 |
0,326 |
10 |
1950 |
405,1 |
351,06 |
684566 |
142202 |
1334904537 |
57601286 |
277294461 |
200,5 |
671,6 |
23,96449892 |
7,812426649 |
0,326 |
11 |
2100 |
379,8 |
351,06 |
737225 |
133317 |
1548173309 |
50628200 |
279966477 |
175,1 |
821,6 |
21,84499146 |
7,121467217 |
0,326 |
12 |
2250 |
352,3 |
205,18 |
461655 |
72293 |
1038723009 |
25471574 |
162658877 |
147,7 |
971,6 |
19,50059383 |
19,50059383 |
1 |
13 |
2250 |
35,67 |
367,91 |
827803 |
13122 |
1862557031 |
467989 |
29523836 |
-169 |
971,6 |
-14,26322214 |
-14,26322214 |
1 |
14 |
2043,75 |
26,37 |
676,53 |
1382648 |
17842 |
2825786786 |
470571 |
36465508 |
-178 |
765,4 |
-16,04992299 |
-5,232274896 |
0,326 |
15 |
1837,5 |
18,12 |
676,53 |
1243115 |
12256 |
2284223238 |
222042 |
22520981 |
-186 |
559,1 |
-17,72632393 |
-5,778781601 |
0,326 |
16 |
1631,25 |
11,06 |
676,53 |
1103581 |
7484 |
1800217169 |
82797 |
12208680 |
-194 |
352,9 |
-19,27442815 |
-6,283463576 |
0,326 |
17 |
1425 |
5,452 |
676,53 |
964048 |
3688 |
1373768578 |
20107 |
5255644 |
-199 |
146,6 |
-20,66871624 |
-6,738001495 |
0,326 |
18 |
1218,75 |
1,611 |
676,53 |
824515 |
1090 |
1004877466 |
1756 |
1328281 |
-203 |
-59,6 |
-21,87423481 |
-7,131000548 |
0,326 |
19 |
1012,5 |
-0,01 |
676,53 |
684982 |
-7,08 |
693543832 |
0,074 |
-7164 |
-205 |
-266 |
-22,84314047 |
-7,446863792 |
0,326 |
20 |
806,25 |
1,221 |
676,53 |
545448 |
826,3 |
439767677 |
1009 |
666198 |
-203 |
-472 |
-23,50782878 |
-7,663552184 |
0,326 |
21 |
600 |
6,272 |
1 335,94 |
801563 |
8380 |
480937500 |
52560 |
5027736 |
-198 |
-678 |
-23,76531217 |
-23,76531217 |
1 |
Расчёт нулевого приближения.
Элемент |
Xi |
Yi |
F пр. i, (0) |
Ф (1) |
F пр. i, (1) |
F*x |
F*y |
F*x^2 |
F*y^2 |
F*x*y |
yi - Y0 |
xi - X0 |
Сигма i фикт. (1) |
Сигма i ист. (1) |
1 |
600 |
469,9 |
1 267 |
1 |
1 267 |
760270 |
595431 |
456161879 |
279799194 |
357258626 |
260,8 |
-539 |
49,89409 |
49,89409 |
2 |
750 |
486,3 |
351,1 |
0,326 |
114,4 |
85834 |
55658 |
64375574 |
27068315 |
41743721 |
277,2 |
-389 |
54,63264 |
17,81024 |
3 |
900 |
494,0 |
351,1 |
0,326 |
114,4 |
103001 |
56533 |
92700826 |
27925867 |
50879769 |
284,8 |
-239 |
57,53444 |
18,75623 |
4 |
1050 |
494,6 |
351,1 |
0,326 |
114,4 |
120168 |
56608 |
126176125 |
27999454 |
59437888 |
285,5 |
-89,4 |
58,97265 |
19,22509 |
5 |
1200 |
489,5 |
351,1 |
0,326 |
114,4 |
137335 |
56026 |
164801469 |
27427259 |
67231337 |
280,4 |
60,57 |
59,21155 |
19,30296 |
6 |
1350 |
479,7 |
351,1 |
0,326 |
114,4 |
154501 |
54897 |
208576859 |
26333245 |
74111440 |
270,5 |
210,6 |
58,44950 |
19,05454 |
7 |
1500 |
465,8 |
351,1 |
0,326 |
114,4 |
171668 |
53306 |
257502295 |
24828364 |
79958494 |
256,6 |
360,6 |
56,84086 |
18,53012 |
8 |
1650 |
448,4 |
351,1 |
0,326 |
114,4 |
188835 |
51318 |
311577777 |
23011279 |
84674691 |
239,3 |
510,6 |
54,50811 |
17,76964 |
9 |
1800 |
428,0 |
351,1 |
0,326 |
114,4 |
206002 |
48988 |
370803305 |
20969057 |
88178204 |
218,9 |
660,6 |
51,54915 |
16,80502 |
10 |
1950 |
405,1 |
351,1 |
0,326 |
114,4 |
223169 |
46358 |
435178879 |
18778019 |
90397994 |
195,9 |
810,6 |
48,04188 |
15,66165 |
11 |
2100 |
379,8 |
351,1 |
0,326 |
114,4 |
240335 |
43461 |
504704499 |
16504793 |
91269071 |
170,6 |
960,6 |
44,04719 |
14,35938 |
12 |
2250 |
352,3 |
205,2 |
1 |
205,2 |
461655 |
72293 |
1038723009 |
25471574 |
162658877 |
143,2 |
1111 |
39,61106 |
39,61106 |
13 |
2250 |
35,67 |
367,9 |
1 |
367,9 |
827803 |
13122 |
1862557031 |
467989 |
29523836 |
-173 |
1111 |
-26,66421 |
-26,66421 |
14 |
2043,75 |
26,37 |
676,5 |
0,326 |
220,5 |
450743 |
5817 |
921206492 |
153406 |
11887756 |
-183 |
904,3 |
-30,39918 |
-9,91013 |
15 |
1837,5 |
18,12 |
676,5 |
0,326 |
220,5 |
405255 |
3996 |
744656776 |
72386 |
7341840 |
-191 |
698,1 |
-33,91765 |
-11,05715 |
16 |
1631,25 |
11,06 |
676,5 |
0,326 |
220,5 |
359768 |
2440 |
586870797 |
26992 |
3980030 |
-198 |
491,8 |
-37,18429 |
-12,12208 |
17 |
1425 |
5,452 |
676,5 |
0,326 |
220,5 |
314280 |
1202 |
447848556 |
6555 |
1713340 |
-204 |
285,6 |
-40,14900 |
-13,08857 |
18 |
1218,75 |
1,611 |
676,5 |
0,326 |
220,5 |
268792 |
355,3 |
327590054 |
572,4 |
433020 |
-208 |
79,32 |
-42,74317 |
-13,93427 |
19 |
1012,5 |
-0,01 |
676,5 |
0,326 |
220,5 |
223304 |
-2,31 |
226095289 |
0,024 |
-2336 |
-209 |
-126,9 |
-44,87289 |
-14,62856 |
20 |
806,25 |
1,221 |
676,5 |
0,326 |
220,5 |
177816 |
269,4 |
143364263 |
329,0 |
217180 |
-208 |
-333,2 |
-46,40546 |
-15,12818 |
21 |
600 |
6,272 |
1 336 |
1 |
1 336 |
801563 |
8380 |
480937500 |
52560 |
5027736 |
-203 |
-539,4 |
-47,13872 |
-47,13872 |
Расчёт первого приближения.
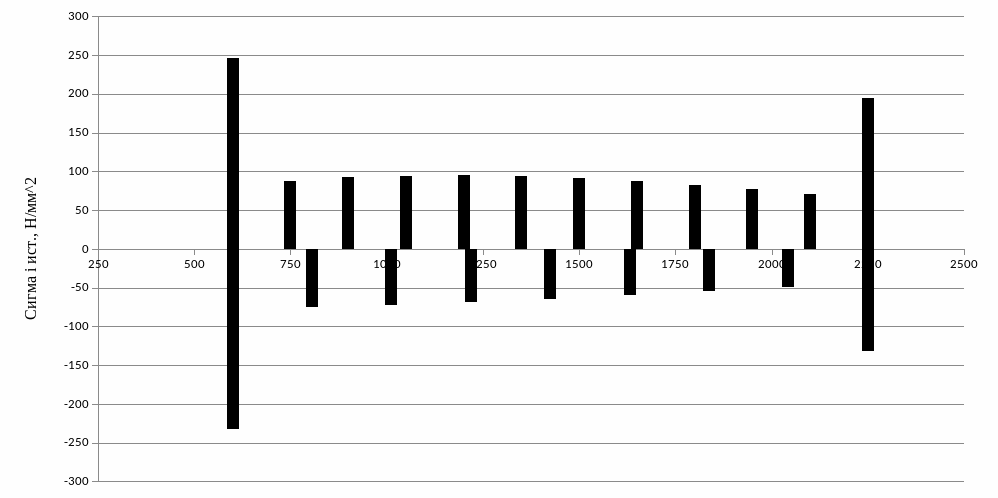
Эпюра нормальных напряжений по силовым элементам сечения крыла.