ЭКЗАМЕН МАТЕМАТИЧЕСКИЙ АНАЛИЗ

1. Предел функции в точке и на бесконечности. Свойства пределов. Односторонние пределы, второе определение предела.

2. Первый замечательный предел и его следствия. Второй замечательный предел и его следствия.

3. Основные теоремы о пределах. Бесконечно малые и их свойства. Третье определение предела. Сравнение бесконечно малых.

4. Непрерывность функции в точке и на отрезке. Точки разрыва и их классификация. Свойства функций, непрерывных на отрезке.

5. Производная, ее геометрический и механический смысл. Уравнение касательной. Свойства производной (правила дифференцирования).

6. Производная сложной, обратной и параметрически заданной функции. Таблица основных производных. Дифференцируемость функции, ее связь с непрерывностью. Дифференциал функции, его геометрический смысл.

Доказательство. При фиксированном значении х₀ будем иметь u₀=u(x₀), у₀=f(u₀). Для нового значения аргумента x₀+Δx:

Δu= u(x₀ + Δx) – u(x₀), Δy=f(u₀+Δu) – f(u₀).

Т.к. u – дифференцируема в точке x₀, то u – непрерывна в этой точке. Поэтому при Δx→0 Δu→0. Аналогично при Δu→0 Δy→0.

По условию . Из этого соотношения, пользуясь определением предела, получаем (при Δu→0)

,

где α→0 при Δu→0, а, следовательно, и при Δx→0.

Перепишем это равенство в виде:

Δy= y '_uΔu+α·Δu.

Полученное равенство справедливо и при Δu=0 при произвольном α, так как оно превращается в тождество 0=0. При Δu=0 будем полагать α=0. Разделим все члены полученного равенства на Δx

.

По условию . Поэтому, переходя к пределу при Δx→0, получим y '_x= y '_u·u '_x . Теорема доказана.

Теорема. Если для функции y=f(x) существует обратная функция x=g(y), которая в некоторой точке у₀ имеет производную g '(v₀), отличную от нуля, то в соответствующей точке x₀=g(x₀) функция y=f(x) имеет производную f '(x₀), равную , т.е. справедлива формула .

Доказательство. Т.к. x=g(y) дифференцируема в точке y₀, то x=g(y) непрерывна в этой точке, поэтому функция y=f(x) непрерывна в точке x₀=g(y₀). Следовательно, при Δx→0 Δy→0.

Покажем, что .

Пусть . Тогда по свойству предела . Перейдем в этом равенстве к пределу при Δy→0. Тогда Δx→0 и α(Δx)→0, т.е. .

Следовательно,

,

что и требовалось доказать.

Таблица основных производных (с доказательством):

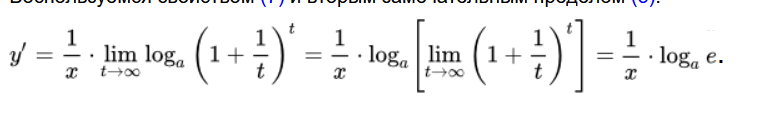
Функция y=f(x) называется дифференцируемой в некоторой точке x₀, если она имеет в этой точке определенную производную, т.е. если предел отношения существует и конечен.

Если функция дифференцируема в каждой точке некоторого отрезка [а; b] или интервала (а; b), то говорят, что она дифференцируема на отрезке [а; b] или соответственно в интервале (а; b).

Теорема. Если функция y=f(x) дифференцируема в некоторой точке x₀, то она в этой точке непрерывна.

Доказательство. Если , то ,

где α бесконечно малая величина, т.е. величина, стремящаяся к нулю при Δx→0. Но тогда

Δy=f '(x₀) Δx+αΔx=> Δy→0 при Δx→0, т.е f(x) – f(x₀)→0 при x→x₀, а это и означает, что функция f(x) непрерывна в точке x₀. Что и требовалось доказать.

Таким образом,из дифференцируемости функции следует ее непрерывность.

Таким образом, в точках разрыва функция не может иметь производной. Обратное утверждение неверно: существуют непрерывные функции, которые в некоторых точках не являются дифференцируемыми т.е. не имеют в этих точках производной (например модуль в нуле)

Определение. Дифференциалом функции в некоторой точке x называется главная, линейная часть приращения функции.

Дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной x (аргумента).

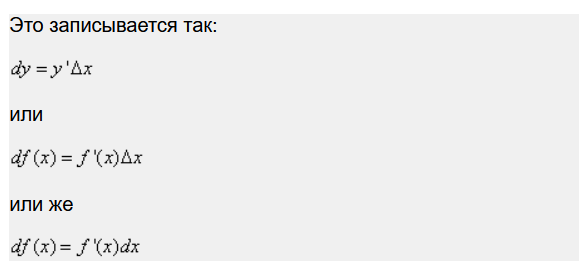
Геометрический смысл дифференциала функции

7. Теоремы Ферма, Ролля, Лагранжа и Коши.

8. Формула Тейлора. Разложение основных элементарных функций по формуле Тейлора. Правило Лопиталя.

9. Условия возрастания и убывания функции. Экстремумы: определение, необходимое условие.

10. Достаточные условия экстремума.

11. Выпуклость вверх и вниз: определение, связь с производными. Точки перегиба: определение, необходимое и достаточное условия существования.

12. Асимптоты графика функции: виды и способы нахождения. Общая схема исследования функции. Производные и дифференциалы высших порядков, их свойства.

13. Комплексные числа, их изображение на плоскости. Алгебраические операции над комплексными числами. Комплексное сопряжение. Модуль и аргумент комплексного числа. Алгебраическая и тригонометрическая формы комплексного числа. Формула Муавра. Корни из комплексных чисел. Формула Эйлера. Показательная форма комплексного числа.

14. Многочлены и их корни. Теорема Безу. Основная теорема алгебры. Разложение многочлена на множители в комплексной и действительной области. Рациональные дроби. Правильная рациональная дробь, ее разложение в сумму простейших в комплексной и действительной области. Интегрирование простейших дробей.

15. Первообразная и ее свойства. Определение неопределенного интеграла. Свойства неопределенного интеграла. Таблица основных интегралов. Замена переменной в неопределенном интеграле. Инвариантность интегрирования. Формула интегрирования по частям.

16. Интегрирование дробно-линейных и квадратичных иррациональностей. Интегрирование рациональных тригонометрических выражений и выражений вида sinnx∙cosmx.

17. Понятие интегральной суммы. Определение определенного интеграла. Необходимое условие интегрируемости. Свойства определенного интеграла.

18. Интегрируемость непрерывных и монотонных ограниченных функций. Производная определенного интеграла по переменному верхнему пределу. Формула Ньютона-Лейбница.

19. Замена переменной и интегрирование по частям в определенном интеграле. Объем тела и площадь поверхности вращения.

20. Площадь фигуры и длина кривой в декартовых и полярных координатах.

21. Несобственные интегралы 1 и 2 рода: определение, понятие сходимости, признак сравнения. Абсолютная сходимость несобственных интегралов 1 рода.

22. Функция нескольких переменных. Геометрическое изображение функции двух переменных. Линии и поверхности уровня. Предел и непрерывность функции нескольких переменных, их свойства.

23. Частные производные, их свойства и геометрический смысл. Дифференцируемость функции нескольких переменных. Дифференциал, его геометрический смысл и свойства. Применение дифференциала к приближенным вычислениям.

24. Дифференцирование сложных функций. Инвариантность формы дифференциала. Неявные функции, условия их существования. Дифференцирование неявных функций.

25. Производная по направлению. Градиент и его свойства. Касательная плоскость и нормаль к поверхности.

Производная по направлению

Пусть функция u = f (x, y, z) непрерывна в некоторой области D и имеет в этой области непрерывные частные производные. Выберем в рассматриваемой области точку M(x,y,z) и проведем из нее вектор S, направляющие косинусы которого , cos, cos. На векторе S на расстоянии Δs от его начала найдем точку М₁(х+Δх, у+Δу, z+Δz), где

При этом

Замечание 1. Частные производные являются частным случаем производной по направлению. Например, при

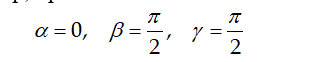
Замечание 2. Выше определялся геометрический смысл частных производных функции двух переменных как угловых коэффициентов касательных к линиям пересечения поверхности, являющейся графиком функции, с плоскостями х = х₀ и у = у₀. Аналогичным образом можно рассматривать производную этой функции по направлению l в точке М(х₀ , у₀) как угловой коэффициент линии пересечения данной поверхности и плоскости, проходящей через точку М параллельно оси Oz и прямой l.

Вектор, координатами которого в каждой точке некоторой области являются частные производные функции u = f (x, y, z) в этой точке, называется градиентом функции u = f (x, y, z).

Обозначение:

Свойства градиента

1. Производная по направлению некоторого вектора S равняется проекции вектора grad u на вектор S.

2 Производная в данной точке по направлению вектора S имеет наибольшее значение, равное |grad u |, если это направление совпадает с направлением градиента.

Доказательство.

Обозначим угол между векторами S и grad u через φ. Тогда из свойства 1 следует, что

следовательно, ее наибольшее значение достигается при φ=0 и равно |gradu|.

3 Производная по направлению вектора, перпендикулярного к вектору grad u , равна нулю.

Доказательство. В этом случае

4 Если z = f (x,y) – функция двух переменных, то

направлен перпендикулярно к линии уровня f (x,y) = c, проходящей через данную точку.

26. Частные производные и дифференциалы высших порядков. Формула Тейлора для функции нескольких переменных.

27. Экстремумы функций нескольких переменных. Необходимое условие экстремума. Достаточное условие экстремума.

28. Условный экстремум. Метод множителей Лагранжа. Нахождение наибольших и наименьших значений функции в ограниченной замкнутой области.

29. Определение числового ряда, частичной суммы, сходимости ряда. Простейшие свойства сходящихся рядов. Необходимое условие сходимости ряда. Остаток ряда, его связь со сходимостью.

30. Критерий сходимости знакоположительных рядов. Интегральный признак Коши. Признаки сравнения.

31. Признак Даламбера. Радикальный признак Коши. Знакопеременные ряды. Абсолютная и условная сходимость. Признак Лейбница. Свойства абсолютно сходящихся рядов.

32. Определение функционального ряда, области сходимости, суммы функционального ряда. Равномерная сходимость функциональных рядов. Признак Вейерштрасса. Свойства равномерно сходящихся рядов.

33. Степенные ряды. 1-я теорема Абеля. Определение радиуса и интервала сходимости степенного ряда. Формулы Даламбера и Коши-Адамара. Свойства степенных рядов.

34. 29. Разложение функции в степенной ряд. Ряды Тейлора и Маклорена. Разложение в ряд Маклорена основных элементарных функций. Формула Эйлера.

35. Двойной и тройной интеграл – определение и свойства.

36. Вычисление двойного интеграла в полярных координатах. Геометрический смысл двойного интеграла.

37. Вычисление двойного интеграла сведением к повторному.

38. Замена переменных в кратных интегралах. Якобиан, его геометрический смысл. Вычисление тройного интеграла в цилиндрической и сферической системах координат.

39. Криволинейный интеграл 1-го рода: определение, свойства, способ вычисления.

40. Криволинейный интеграл 2-го рода: определение, свойства, способ вычисления. Условия независимости криволинейного интеграла 2-го рода от пути интегрирования.

41. Поверхностный интеграл 1-го рода: определение, свойства, способ вычисления.

42. Поверхностный интеграл 2-го рода: определение, свойства, способ вычисления.

43. Формулы Грина, Стокса и Гаусса-Остроградского.

44. Геометрические и физические приложения кратных, криволинейных и поверхностных интегралов.