
Лабы / 3 лаб
.docx
Лабораторный практикум по ДЦКС
Лабораторная 3.
Выполнили:
Студенты группы
РФ-31БО
Ярославль 2022
Ход работы
Исследовать колебательные процессы в системе 2-ого порядка в некритических условиях.
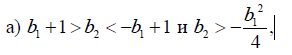
Первая подходящая точка b1 = -0.5, b2 = 0.
Вторая подходящая точка b1 = -0.4, b2 = 0.2.
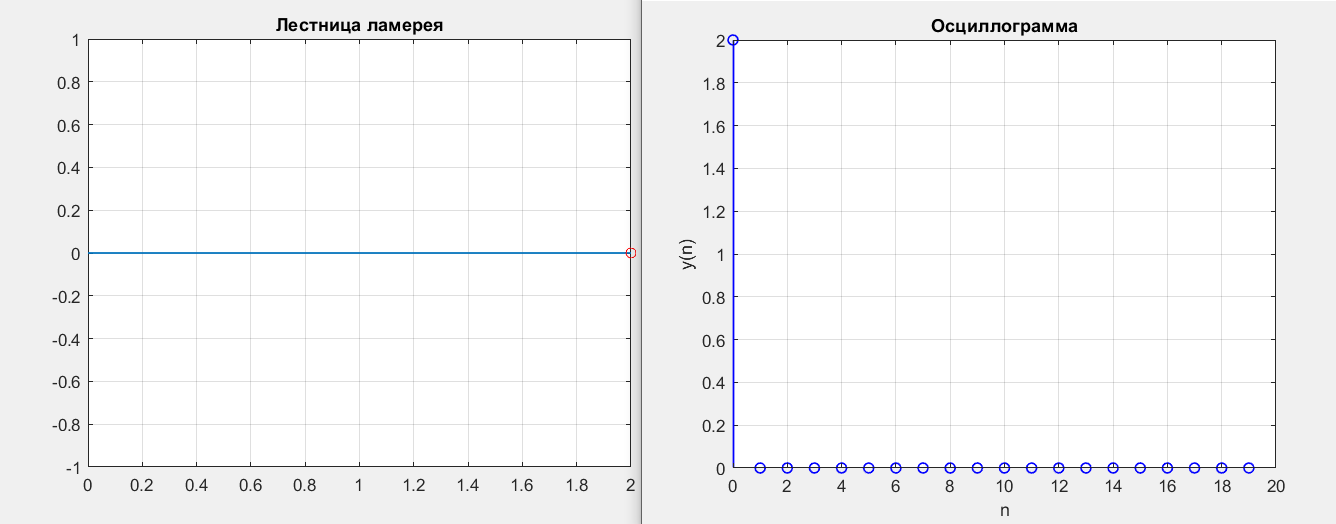
Рисунок 1 – y(0) = 2; b1 = -0.5; b2 = 0
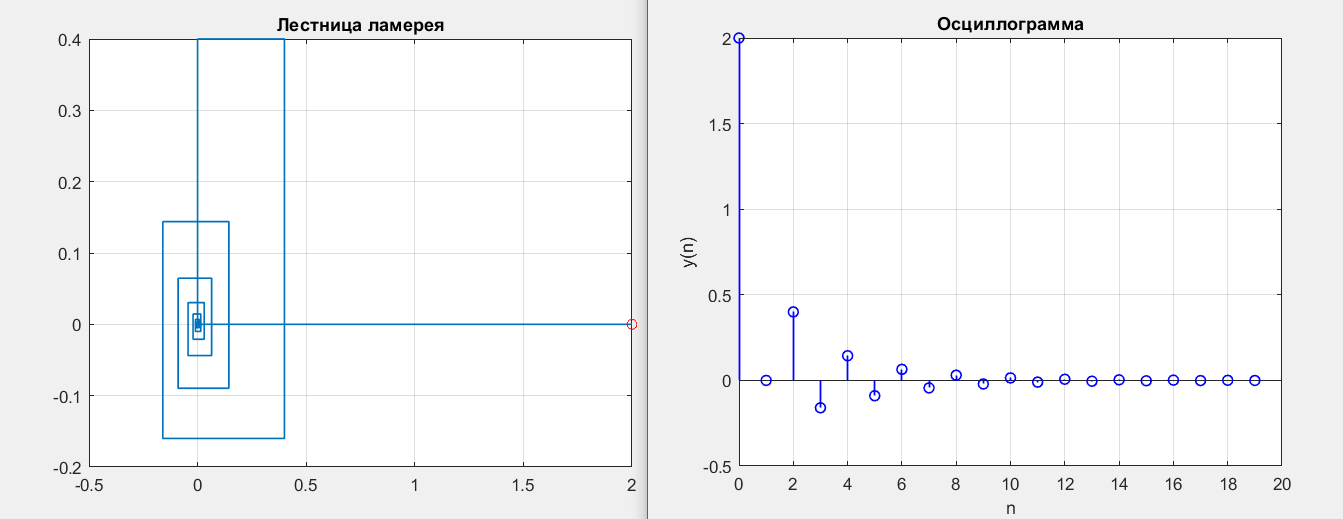
Рисунок 2 – y(0) = 2; b1 = -0.4; b2 = 0.2
Получились точки типа устойчивый фокус.

Первая подходящая точка b1 = 0, b2 =-0.2.
Вторая подходящая точка b1 = 1, b2 =-0.8.
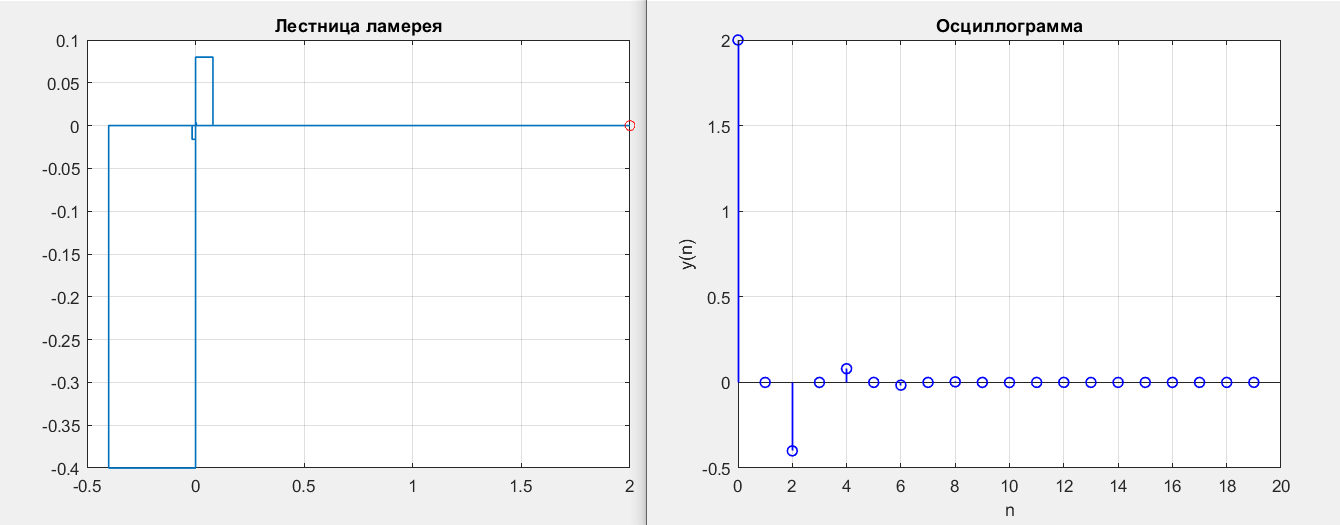
Рисунок 3 – y(0) = 2; b1 = 0; b2 =-0.2

Рисунок 4 – y(0) = 2; b1 = 1; b2 =-0.8
Получилась точки типа устойчивый фокус.
![]()
Первая подходящая точка b1 = 0, b2 =1.2.
Вторая подходящая точка b1 = 0.5, b2 =1.6.
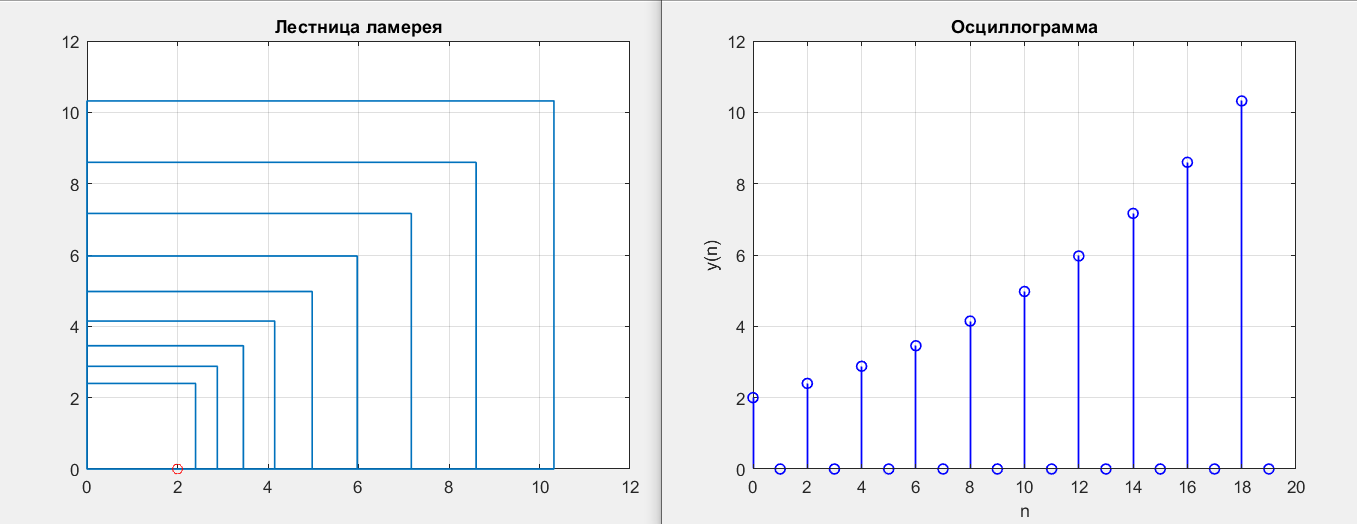
Рисунок 5 – y(0) = 2; b1 = 0; b2 = 1.2
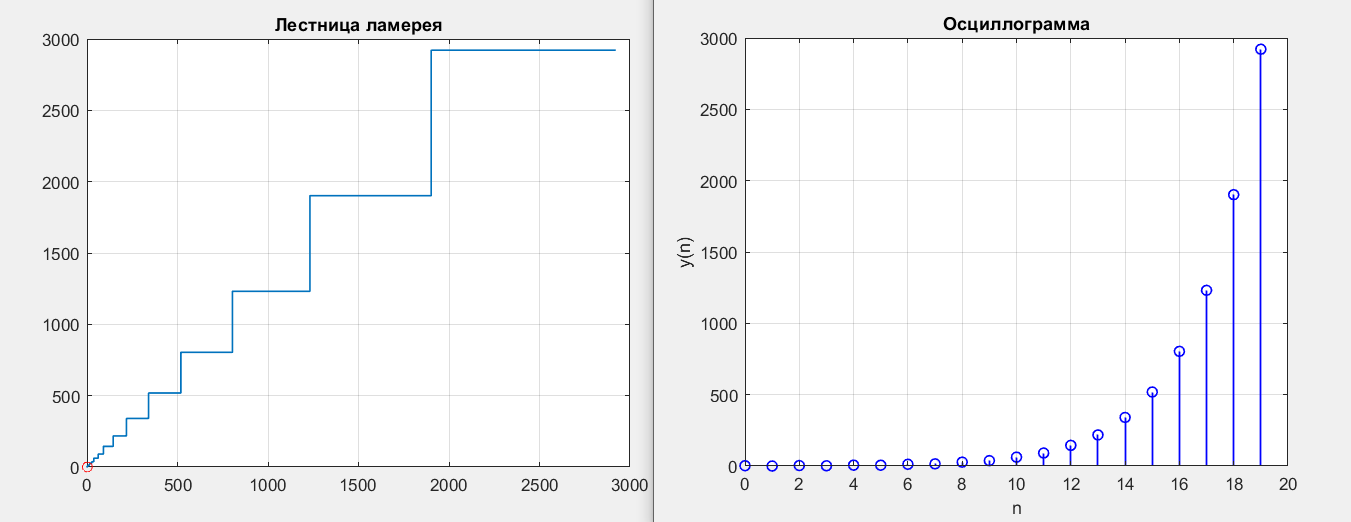
Рисунок 6 – y(0) = 2; b1 = 0.5; b2 =1.6
Получилась точки типа неустойчивый узел.
![]()
Первая подходящая точка b1 = 2.1, b2 = -1.1.
Вторая подходящая точка b1 = 3 b2 =-2.
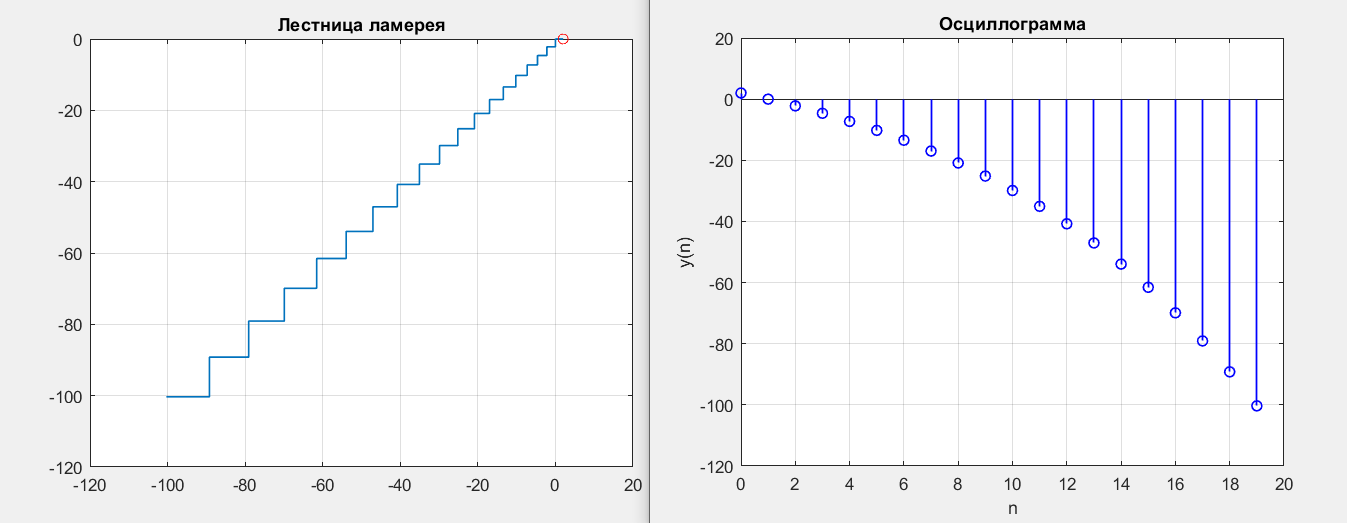
Рисунок 7 – y(0) = 2; b1 = 2.1; b2 = -1.1
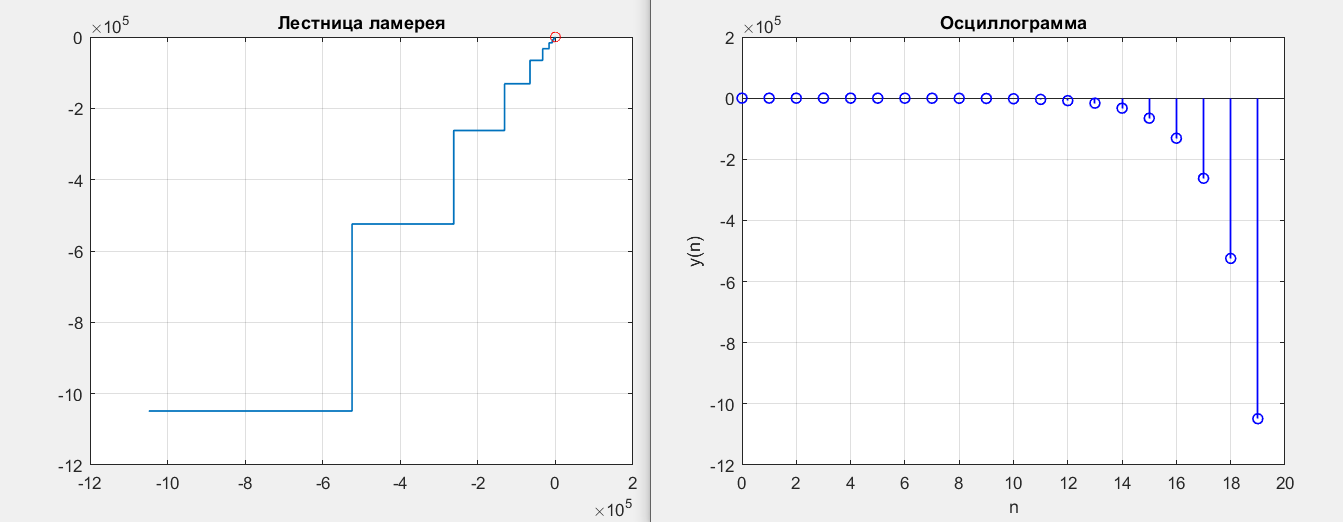
Рисунок 8 – y(0) = 2; b1 = 3; b2 = -2
Получились точки типа неустойчивый узел.
![]()
Первая подходящая точка b1 = -2.1, b2 = -1.1.
Вторая подходящая точка b1 = -2.5, b2 =-1.3.

Рисунок 9 – y(0) = 2; b1 = -2.1; b2 = -1.1
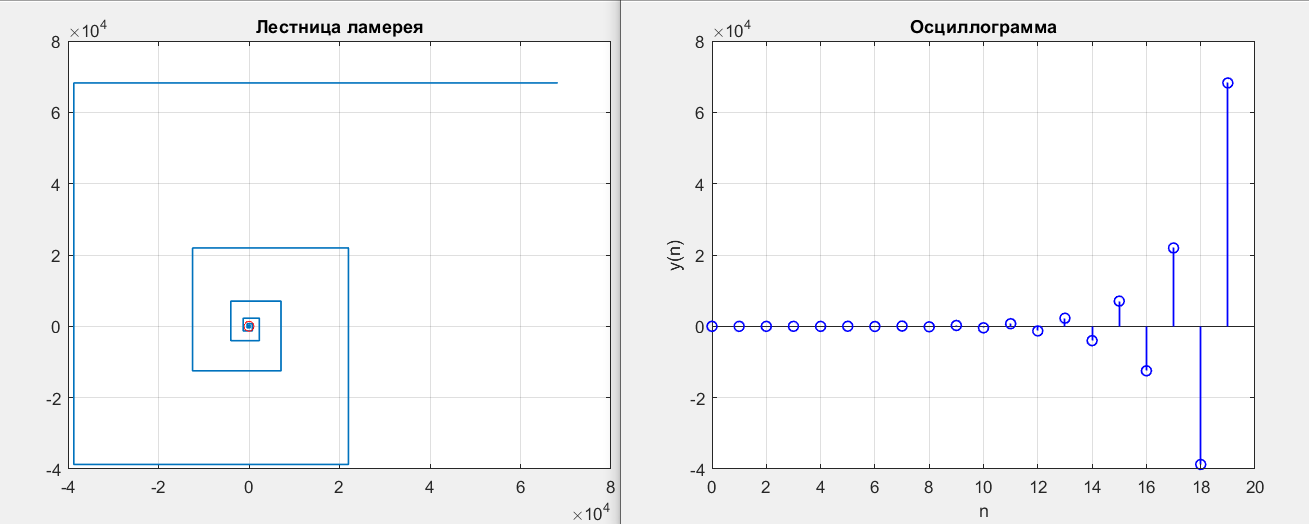
Рисунок 10 – y(0) = 2; b1 = -2.5; b2 = -1.3
Получились точки типа неустойчивый фокус.
![]()
Первая подходящая точка b1 = -1.5, b2 = 0.8.
Вторая подходящая точка b1 = -0.5, b2 =1.2.

Рисунок 11 – y(0) = 2; b1 = -1.5; b2 = 0.8
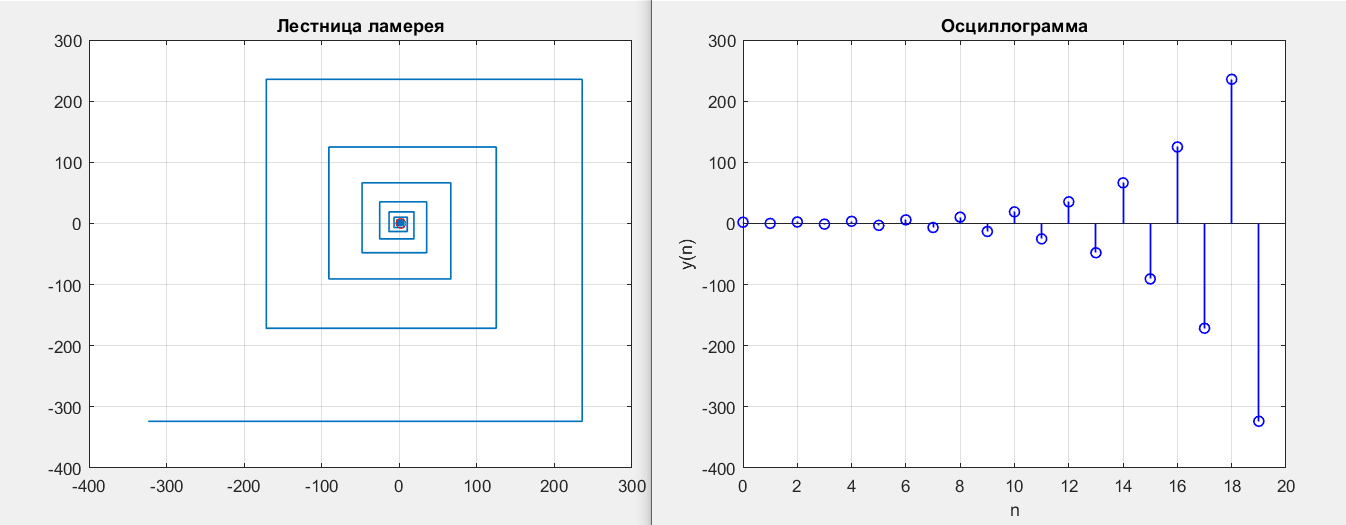
Рисунок 12 – y(0) = 2; b1 = -0.5; b2 = 1.2
Получились точки типа неустойчивый фокус.
![]()
Первая подходящая точка b1 = 1.5, b2 = 0.8.
Вторая подходящая точка b1 = 0.5, b2 =1.2.
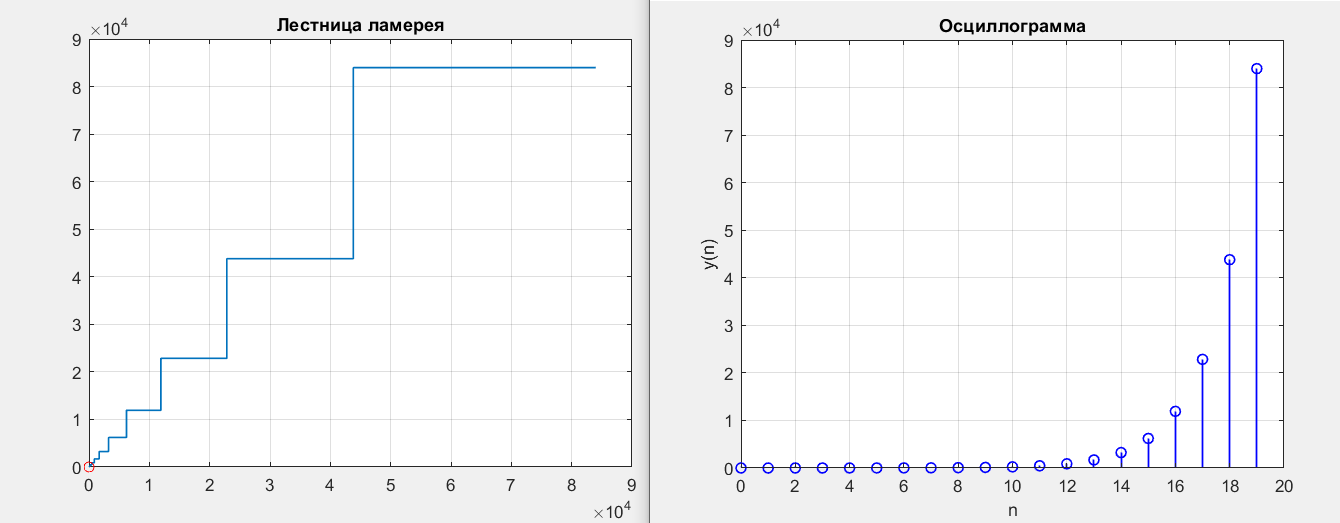
Рисунок 13 – y(0) = 2; b1 = -1.5; b2 = 0.8
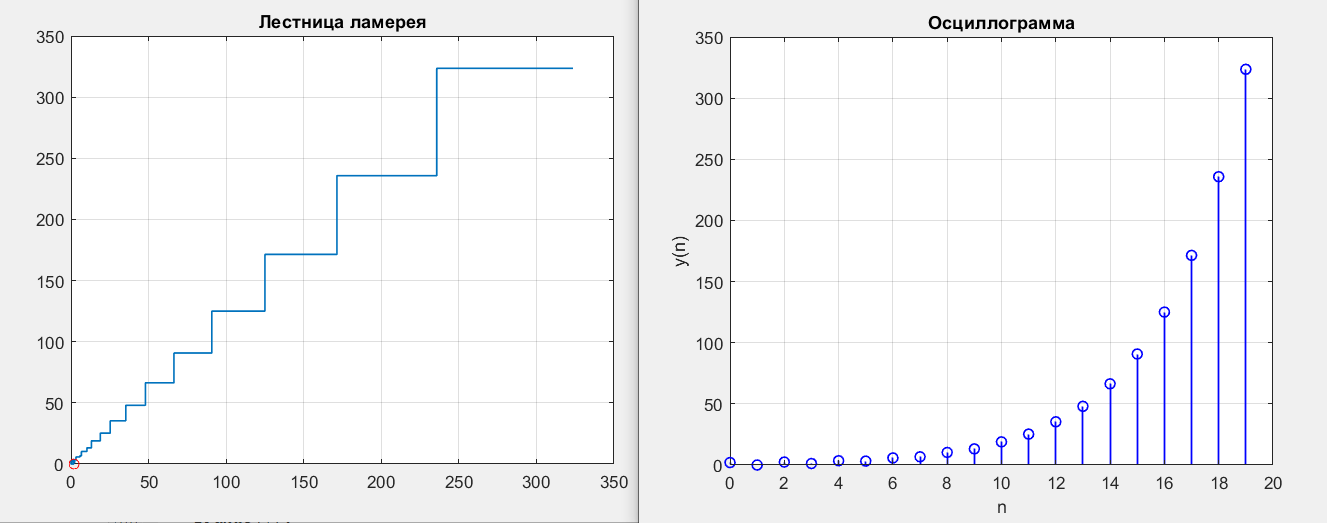
Рисунок 14 – y(0) = 2; b1 = -0.5; b2 = 1.2
Получились точки типа седло.
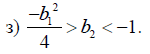
Первая подходящая точка b1 = 0, b2 =-1.5.
Вторая подходящая точка b1 = -2, b2 =-2.
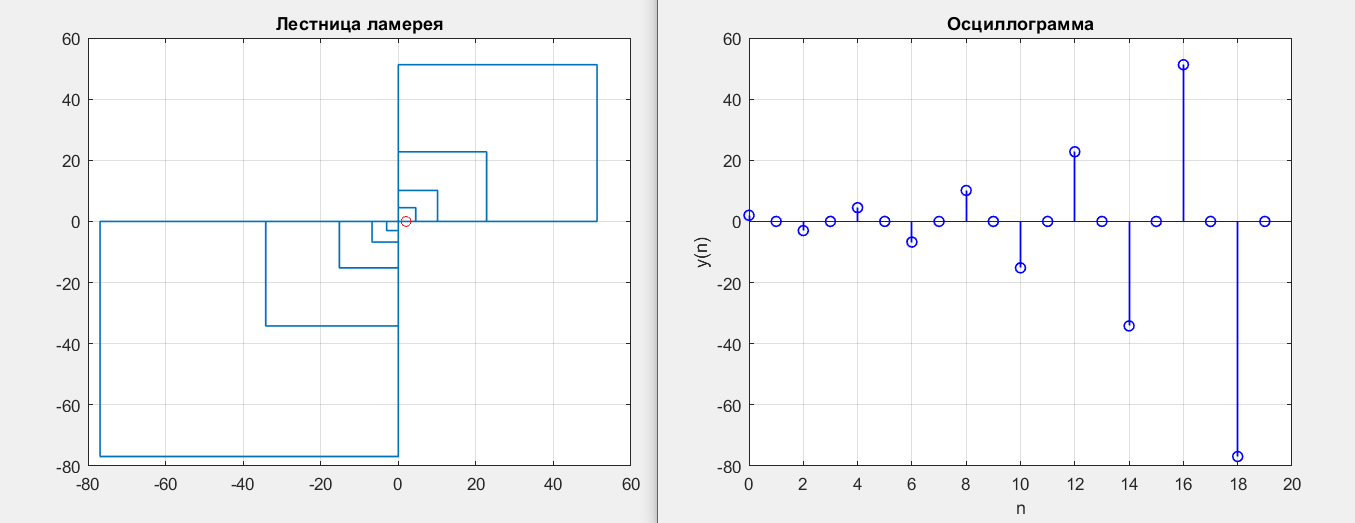
Рисунок 15 – y(0) = 2; b1 = 0; b2 = -1.5
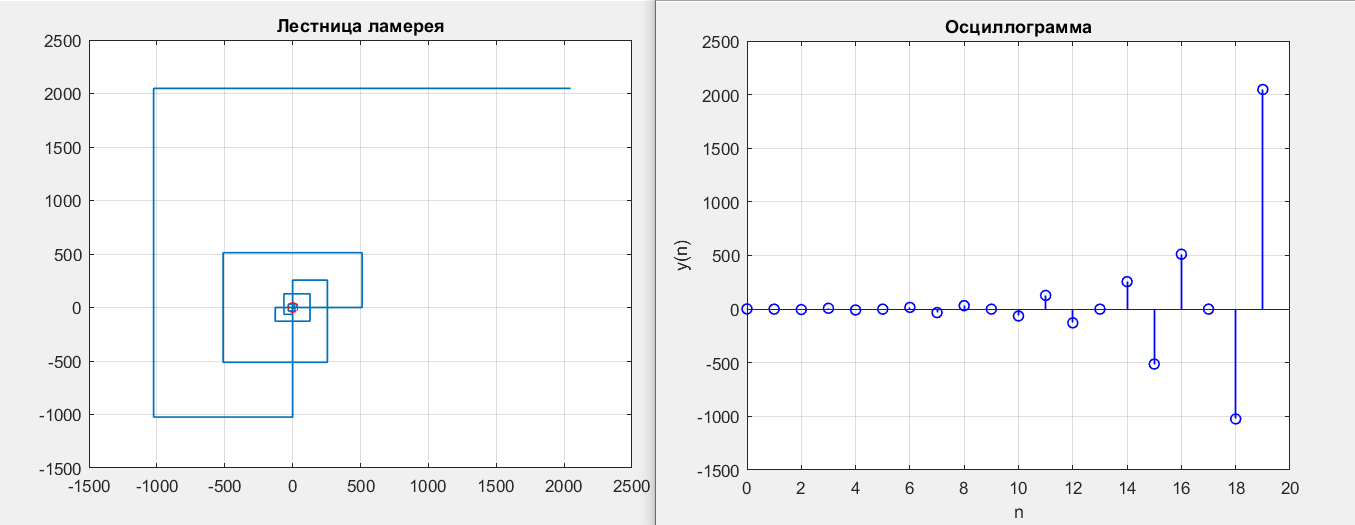
Рисунок 16 – y(0) = 2; b1 = -2; b2 =-2
Получились точки типа неустойчивый фокус.
Исследовать колебательные процессы в системе 2-ого порядка в критических условиях.

Рисунок 17 – y(0) = 2; b1 = -2; b2 =-1, период 2 точка типа неустойчивый фокус
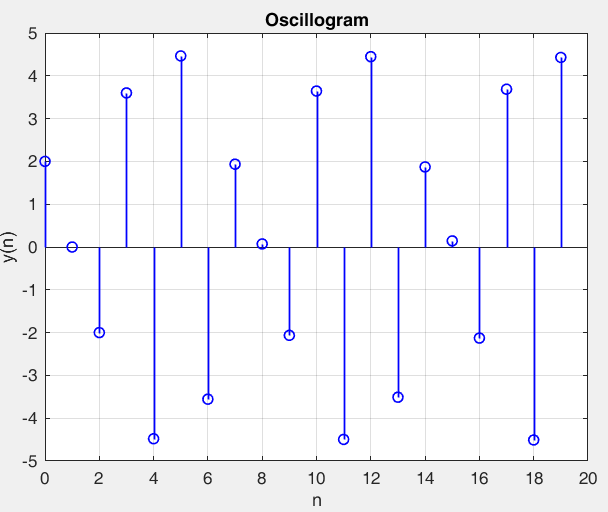

Рисунок 18 – y(0) = 2; b1 = -1.8; b2 =-1, период 7 точка типа центр
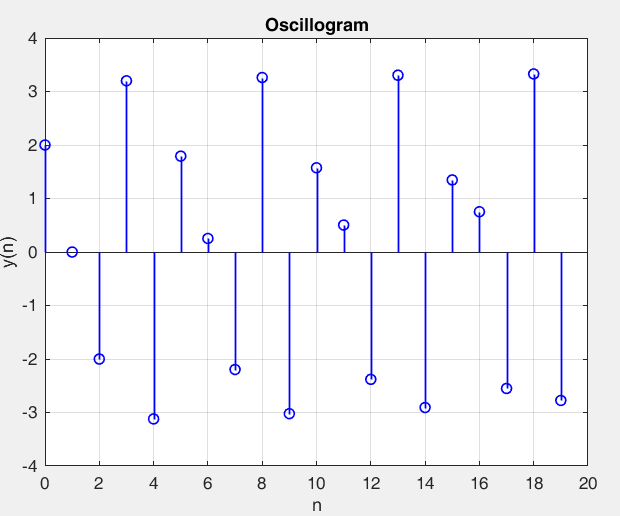
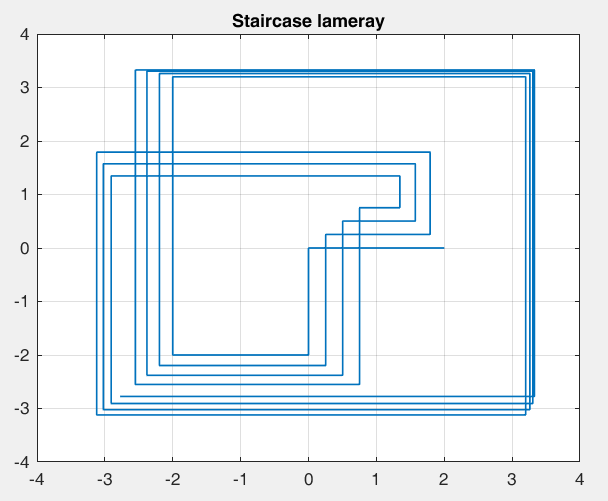
Рисунок 19 – y(0) = 2; b1 = -1.6; b2 =-1, период 5 точка типа центр
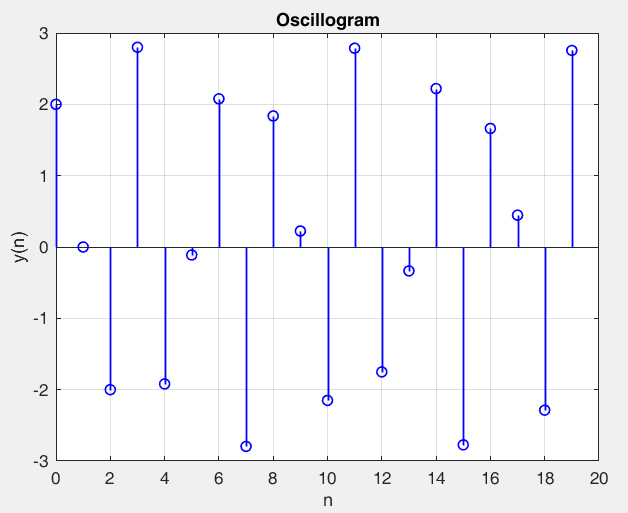

Рисунок 20 – y(0) = 2; b1 = -1.4; b2 =-1, период 8 точка типа центр
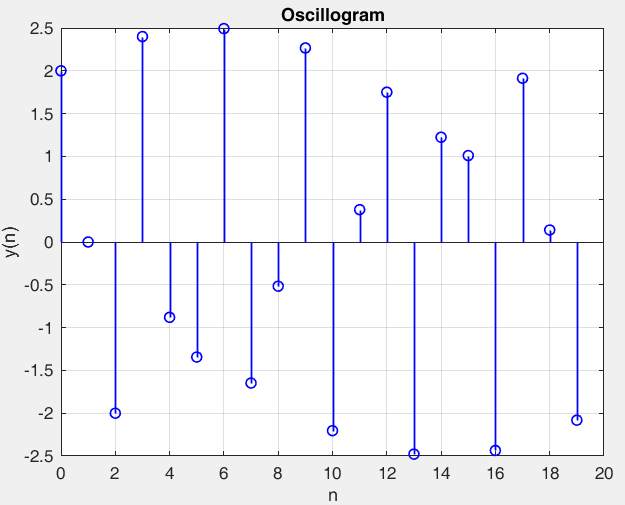
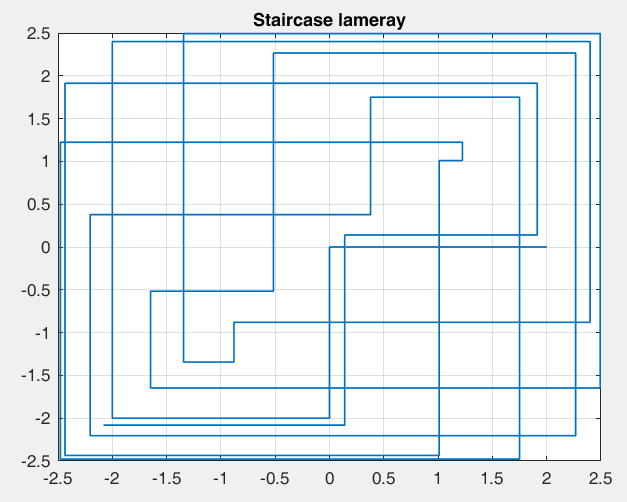
Рисунок 21 – y(0) = 2; b1 = -1.2; b2 =-1, период 14 точка типа центр
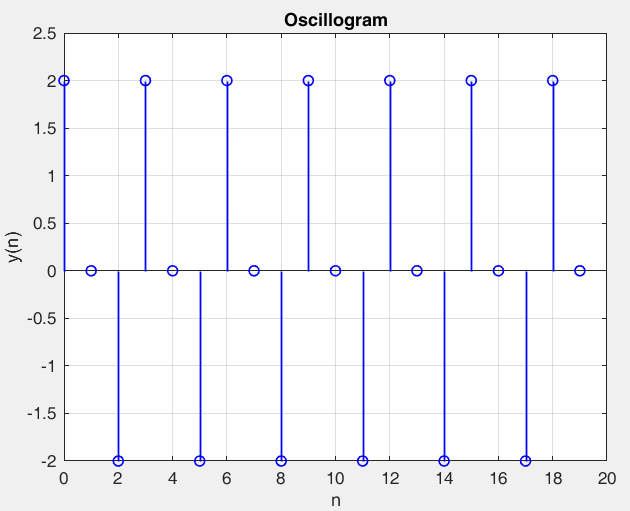
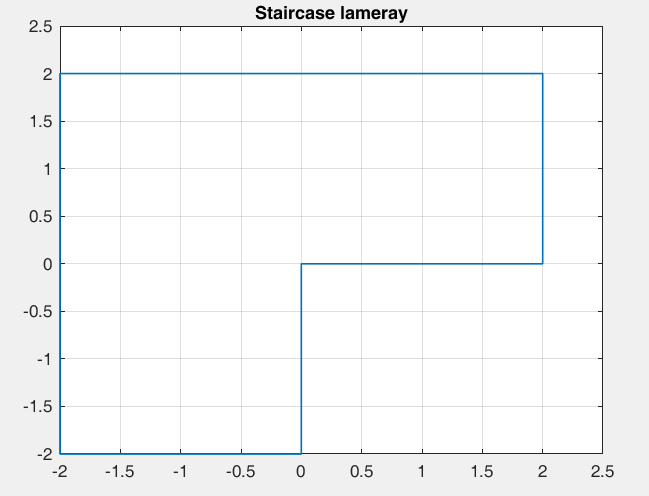
Рисунок 22 – y(0) = 2; b1 = -1.0; b2 =-1, период 2 точка типа центр
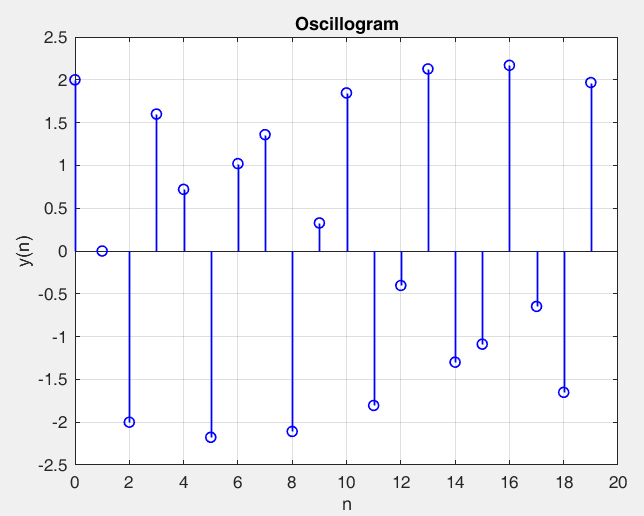
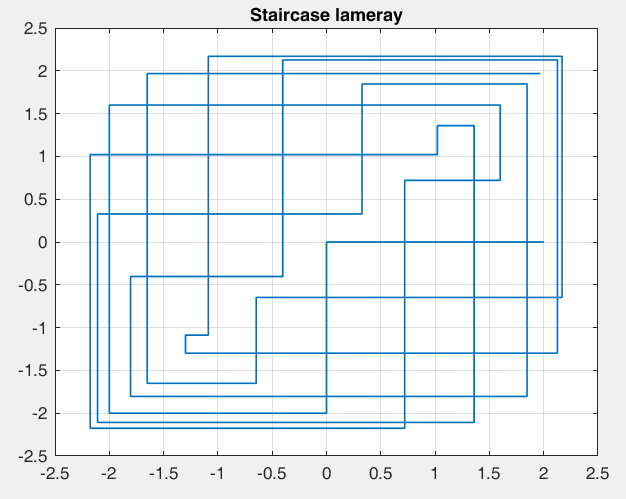
Рисунок 23 – y(0) = 2; b1 = -0.8; b2 =-1, точка типа центр
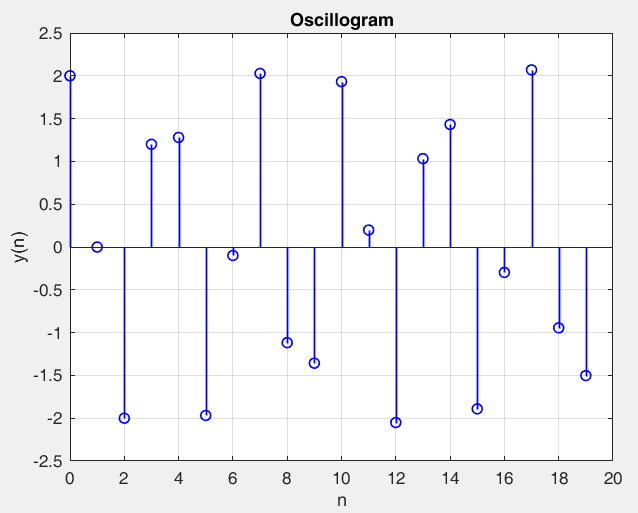
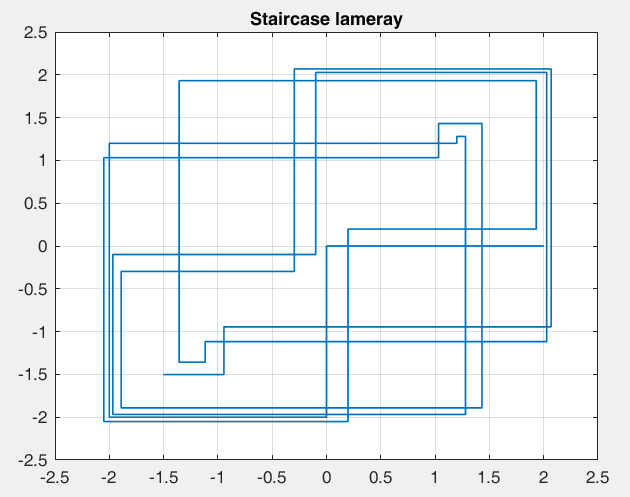
Рисунок 24 – y(0) = 2; b1 = -0.6; b2 =-1, точка типа центр
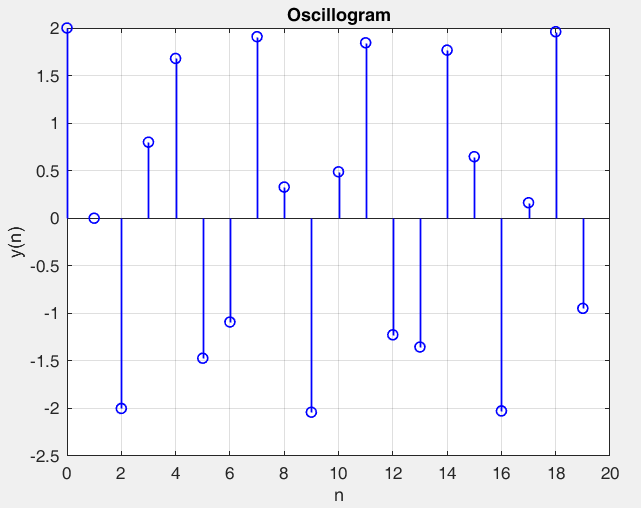
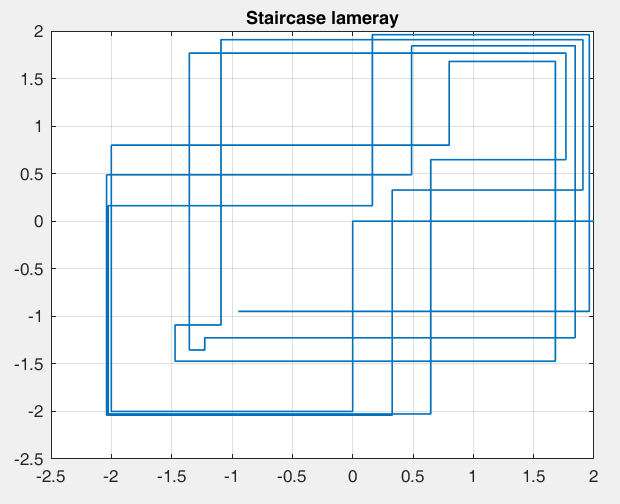
Рисунок 25 – y(0) = 2; b1 = -0.4; b2 =-1, период 18 точка типа центр
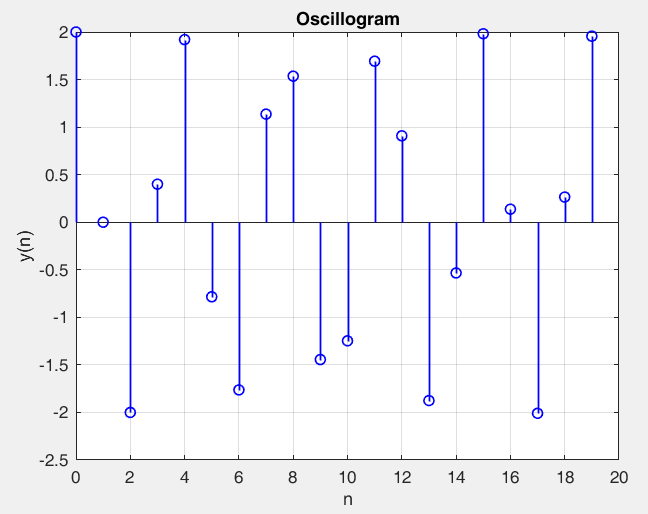
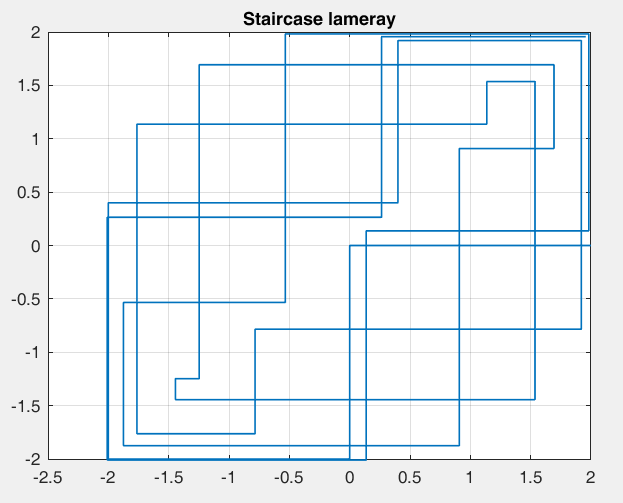
Рисунок 26 – y(0) = 2; b1 = -0.2; b2 =-1, период 15 точка типа центр
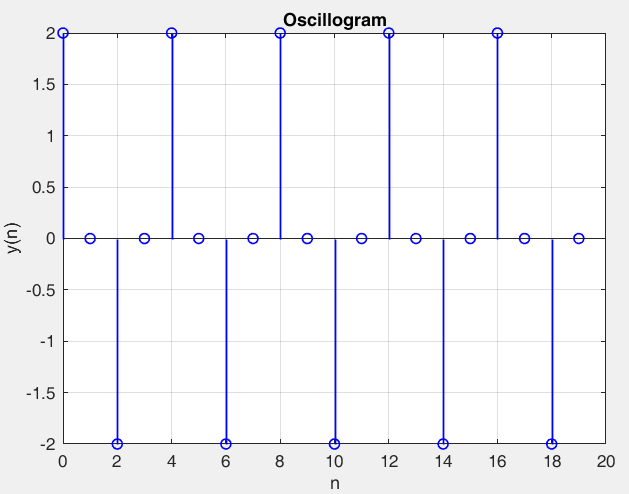
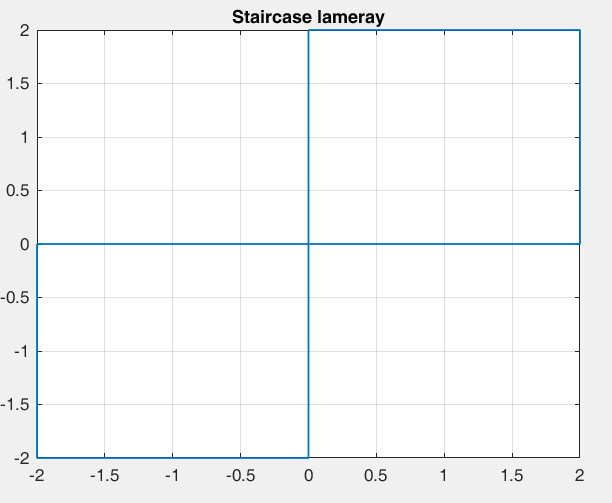
Рисунок 27 – y(0) = 2; b1 = 0; b2 =-1, период 2 точка типа центр
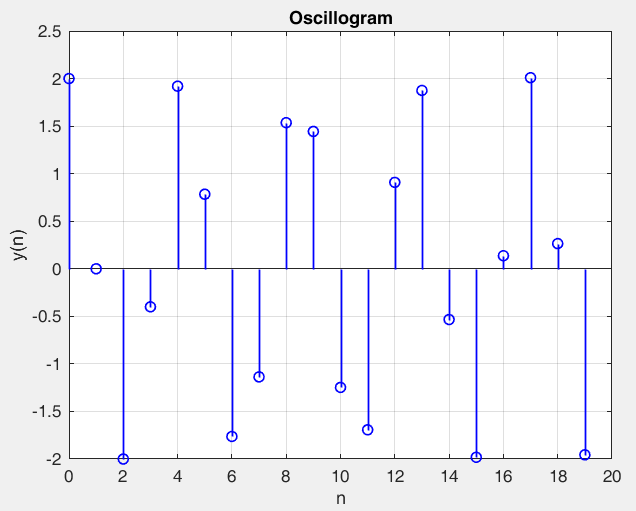
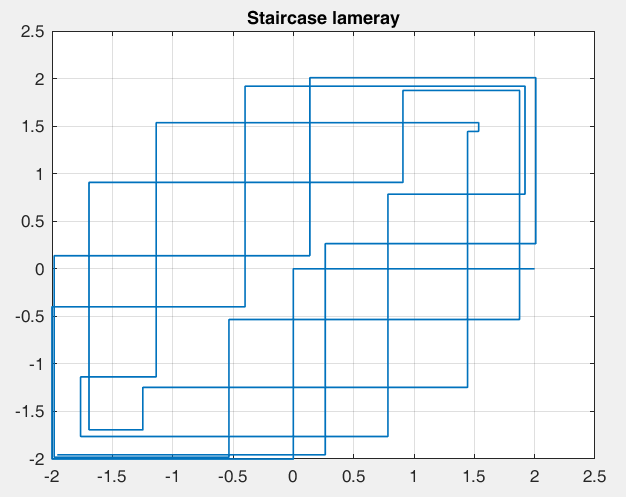
Рисунок 28 – y(0) = 2; b1 = 0.2; b2 =-1, точка типа центр
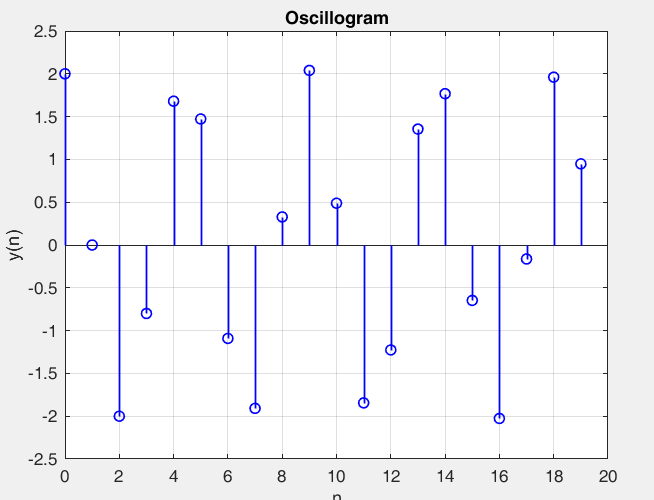
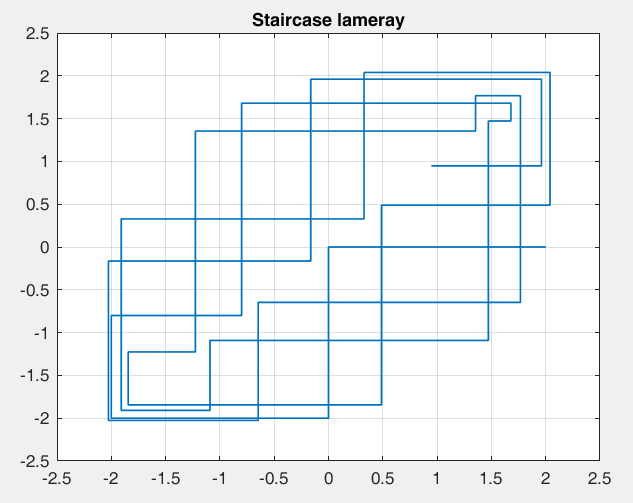
Рисунок 29 – y(0) = 2; b1 = 0.4; b2 =-1, точка типа нцентр
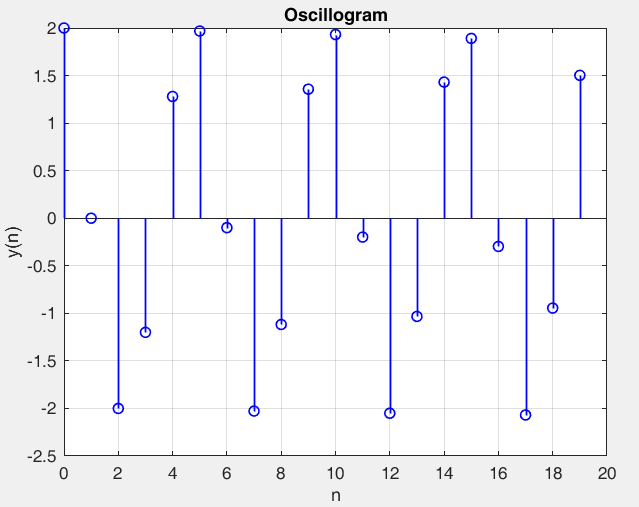

Рисунок 30 – y(0) = 2; b1 = 0.6; b2 =-1, период 5 точка типа центр
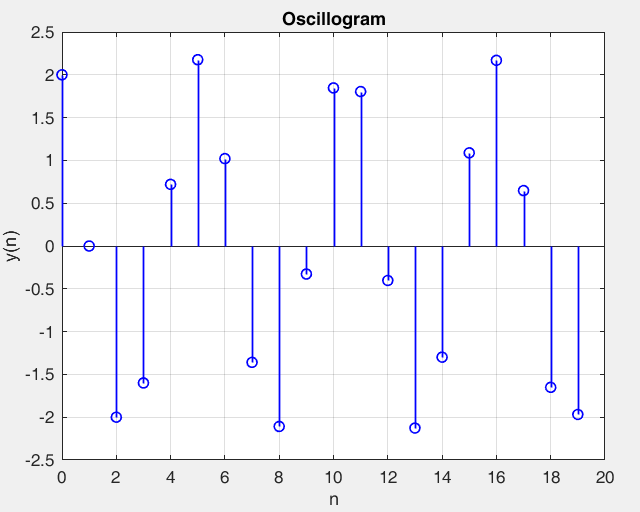
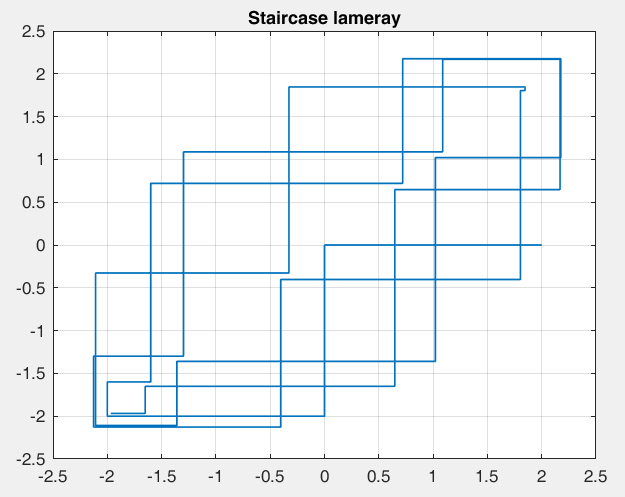
Рисунок 31 – y(0) = 2; b1 = 0.8; b2 =-1, точка типа центр
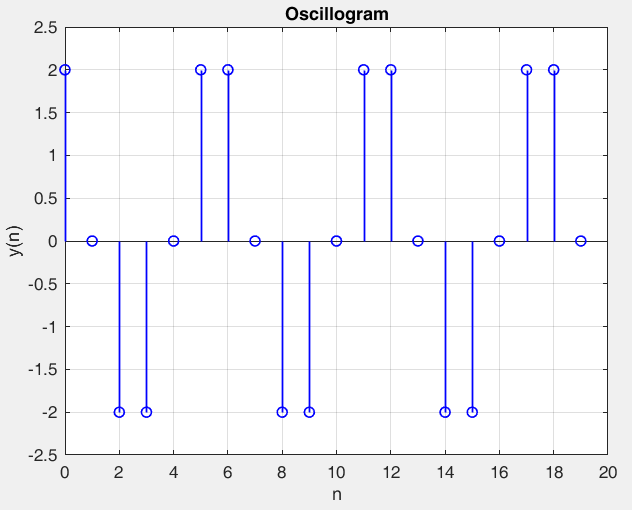
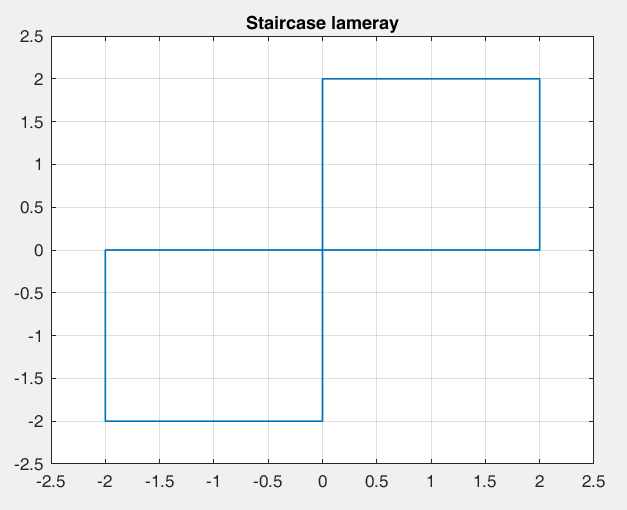
Рисунок 32 – y(0) = 2; b1 = 1; b2 =-1, период 6 точка типа центр
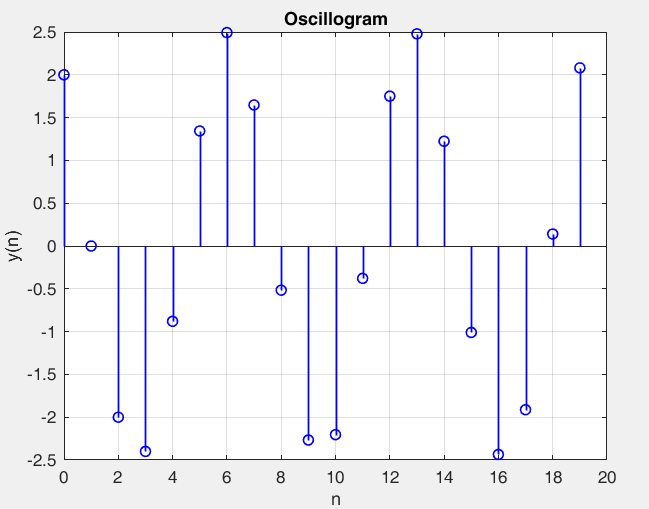
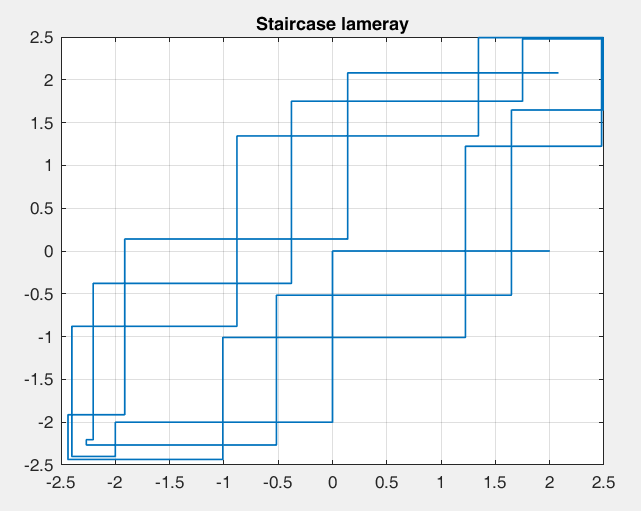
Рисунок 33 – y(0) = 2; b1 = 1.2; b2 =-1, точка типа центр
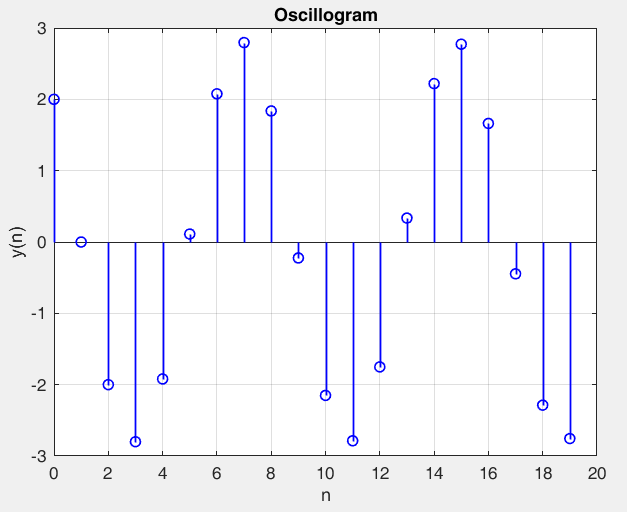
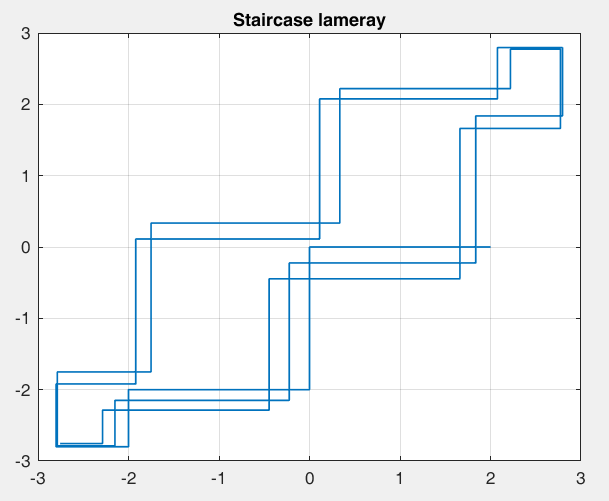
Рисунок 34 – y(0) = 2; b1 = 1.4; b2 =-1, период 8 точка типа центр
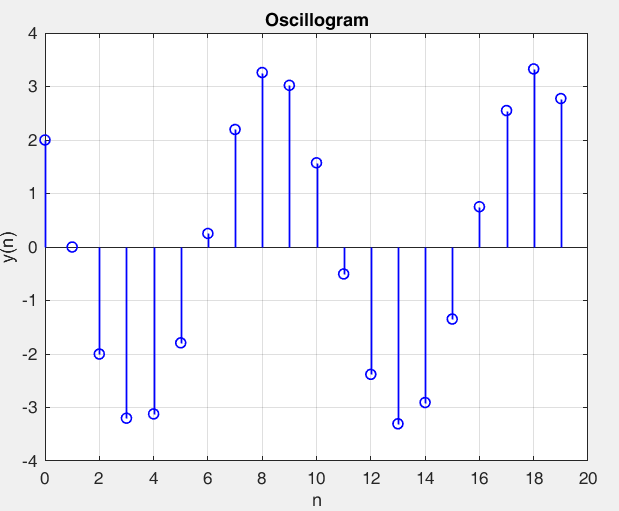
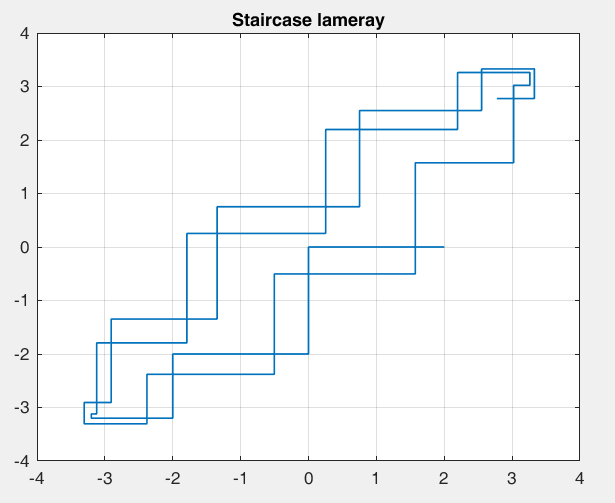
Рисунок 35 – y(0) = 2; b1 = 1.6; b2 =-1, период 10 точка типа центр

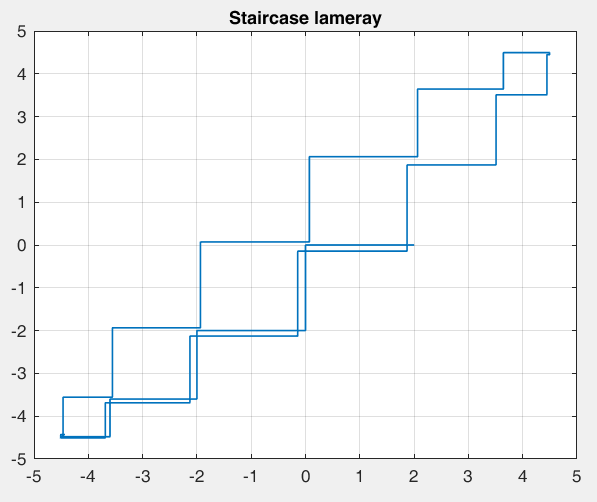
Рисунок 36 – y(0) = 2; b1 = 1.8; b2 =-1, период 14 точка типа центр

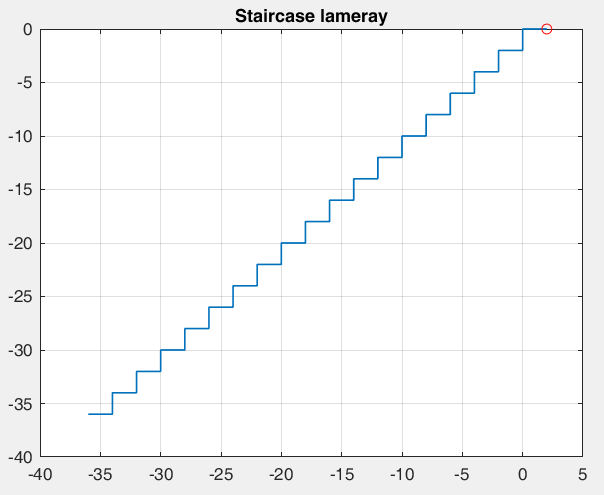
Рисунок 37 – y(0) = 2; b1 = 2.0; b2 =-1, точка типа седло/неустойчивый узел
Вывод
Таким образом из получившихся данных мы рассмотрели различные виды особых точек в системе 2 порядка. При этом рассмотрели области параметров b1 и b2 в которых находятся определённые точки и они совпали.
