
- •Электрон, его заряд и масса.
- •Движение электронов в электрическом поле.
- •Расчёт удельного заряда электрона через его отклонение в магнитном поле.
- •Определение удельного заряда электрона методом компенсации отклонения электронного пучка в электрическом и магнитном полях.
- •Метод фильтрации частиц по скорости.
Расчёт удельного заряда электрона через его отклонение в магнитном поле.
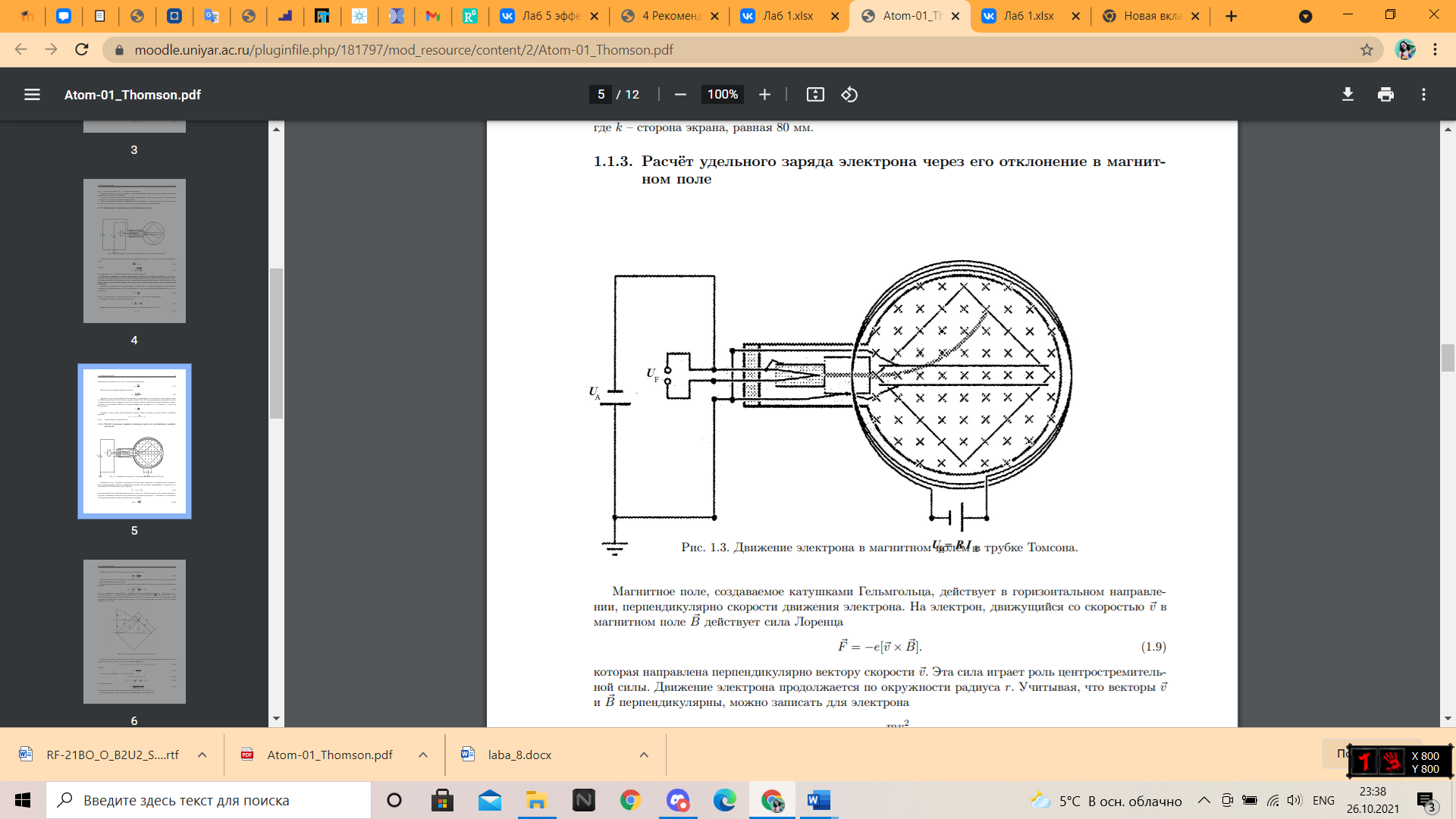
Рисунок 3 - Движение электрона в магнитном полем в трубке Томсона.
Магнитное поле, создаваемое катушками
Гельмгольца, действует в горизонтальном
направлении, перпендикулярно скорости
движения электрона. На электрон,
движущийся со скоростью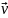 в магнитном поле
в магнитном поле
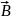 действует сила Лоренца
действует сила Лоренца
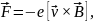 (11)
(11)
которая направлена перпендикулярно
вектору скорости
.
Эта сила играет роль центростремительной
силы. Движение электрона продолжается
по окружности радиуса
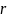 .
Учитывая, что векторы
и
перпендикулярны, можно записать для
электрона:
.
Учитывая, что векторы
и
перпендикулярны, можно записать для
электрона:
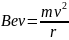 (12)
(12)
Из формул (12) и (3) можно получить значение :
 (13)
(13)
Для вычисления
необходимо определить индукцию магнитного
поля
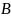 и радиус траектории
непосредственно из эксперимента.
и радиус траектории
непосредственно из эксперимента.
Индукция магнитного поля , создаваемая катушками Гельмгольца, может быть определена по формуле:
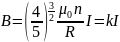 ,
(14)
,
(14)
где:
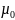 – магнитная постоянная,
– магнитная постоянная,
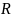 – средний радиус катушки Гельмгольца,
– средний радиус катушки Гельмгольца,
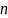 - число витков,
- число витков,
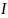 – ток в катушках,
– эмпирический коэффициент, численно
равный
– ток в катушках,
– эмпирический коэффициент, численно
равный
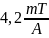 . Ток в катушках
,
при отсутствии амперметра, можно
определить по закону Ома, исходя из
того, что сопротивление одной катушки
. Ток в катушках
,
при отсутствии амперметра, можно
определить по закону Ома, исходя из
того, что сопротивление одной катушки
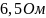 и они соединены параллельно, т. е. их
сопротивление составляет
и они соединены параллельно, т. е. их
сопротивление составляет
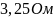 .
Таким образом,
.
Таким образом,
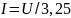 .
.
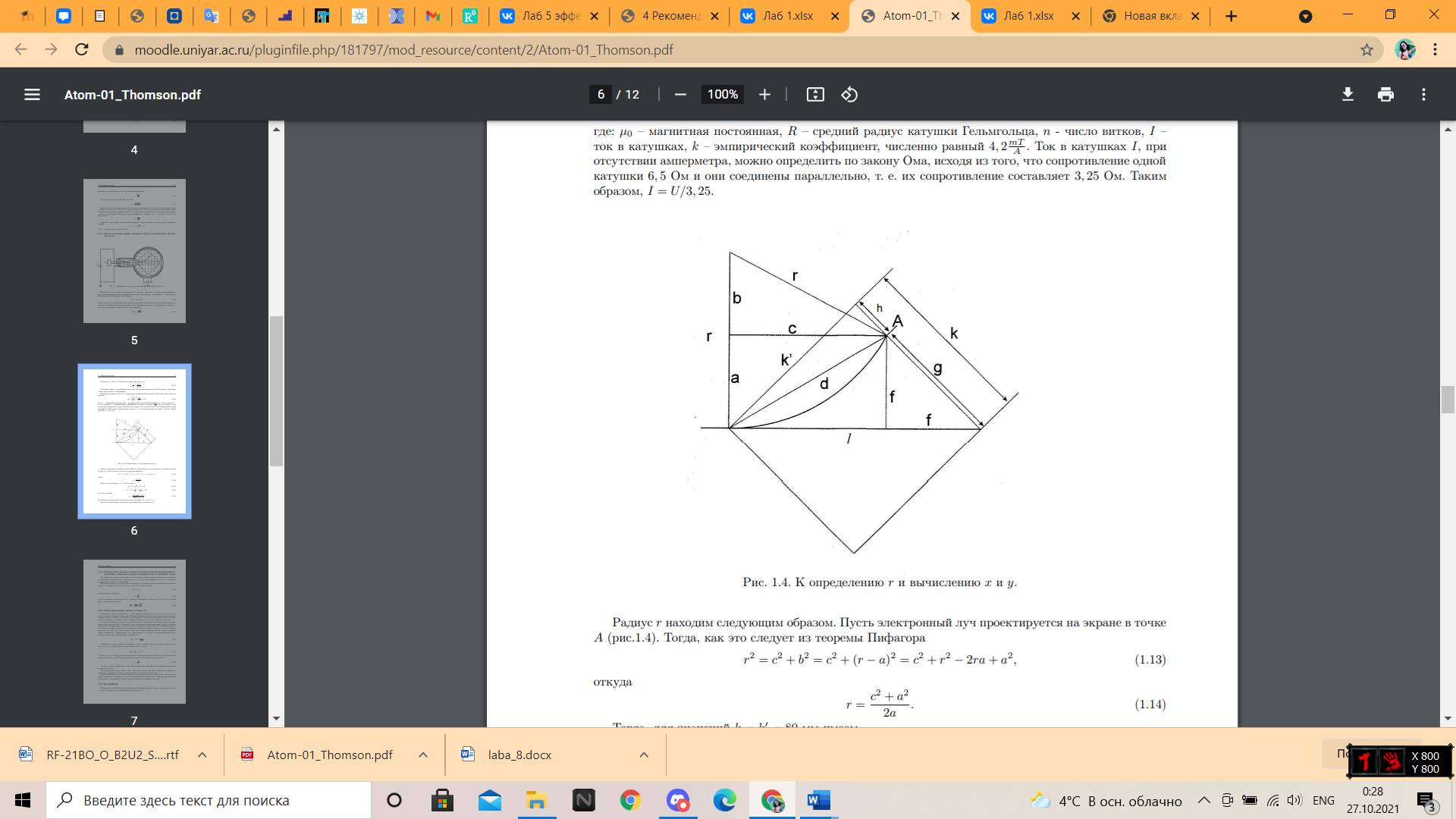
Рисунок 4 - К определению r и вычислению x и y
Радиус
находим следующим образом. Пусть
электронный луч проектируется на экране
в точке
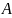 (рисунок 4). Тогда, как это следует из
теоремы Пифагора
(рисунок 4). Тогда, как это следует из
теоремы Пифагора
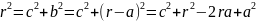 ,
(15)
,
(15)
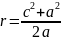 (16)
(16)
Тогда, для значений
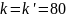 мм имеем:
мм имеем:
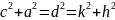 (17)
(17)
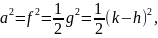 (18)
(18)
 (19)
(19)
где значение
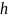 можно взять непосредственно на экране
можно взять непосредственно на экране
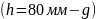 .
По этим данным можно определить удельный
заряд электрона
.
По этим данным можно определить удельный
заряд электрона
Определение удельного заряда электрона методом компенсации отклонения электронного пучка в электрическом и магнитном полях.
Указанный метод является частным случаем компенсационного метода измерений, где ряд величин обращается в нуль и, тем самым, уменьшаются погрешности измерений.
Необходимо добиться условий, когда отклонение электронного пучка в магнитном поле компенсируется электрическим полем. В этом случае выполняется условие:
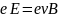 (20)
(20)
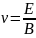 (21)
(21)
где
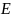 определяется из формулы (4). Значение
находится по формуле (14), тогда удельный
заряд электрона будет равен:
определяется из формулы (4). Значение
находится по формуле (14), тогда удельный
заряд электрона будет равен:
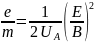 (22)
(22)
Метод фильтрации частиц по скорости.
Самый простой фильтр скоростей устроен
так: пучок заряженных частиц пропускают
одновременно через электрическое и
магнитное поля, направленные перпендикулярно
друг другу таким образом, что они
отклоняют частицы в противоположных
направлениях. Если выбрать направление
полей так, чтобы обе силы были направлены
в противоположные стороны, то их
результирующая будет
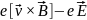 . Под влиянием этой силы частица движется
по кривой с радиусом кривизны
.
Приравнивая силу, действующую на частицу
к центростремительной силе, получаем
в проекции на направление действия сил
. Под влиянием этой силы частица движется
по кривой с радиусом кривизны
.
Приравнивая силу, действующую на частицу
к центростремительной силе, получаем
в проекции на направление действия сил
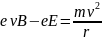 (23)
(23)
Очевидно, что через конденсатор пройдут
только частицы, скорость которых такова,
что обе силы
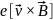 и
и
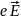 друг друга компенсируют. В этом случае:
друг друга компенсируют. В этом случае:
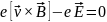 (24)
(24)
С учётом того, что направления электрического и магнитного полей выбраны таким образом, что кулоновская сила и сила Лоренца направлены вдоль одной прямой, можем записать:
(25)
Ход работы.
Общий вид и устройство лабораторной установки «Трубка Томсона» показано на рисунке 5. Схема электрических соединений приведена на рисунке 6.
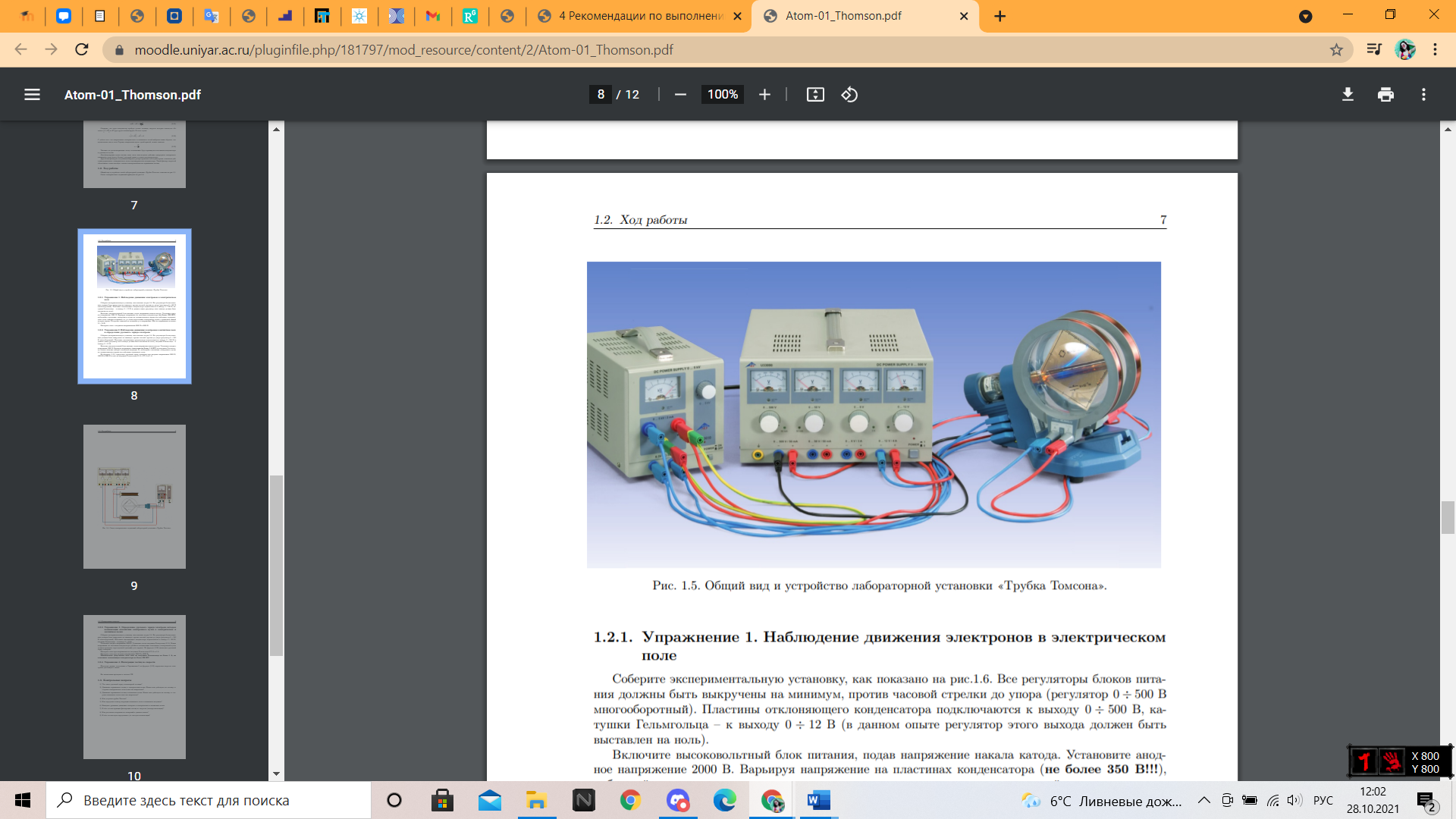
Рисунок 5 - Общий вид и устройство лабораторной установки «Трубка Томсона».
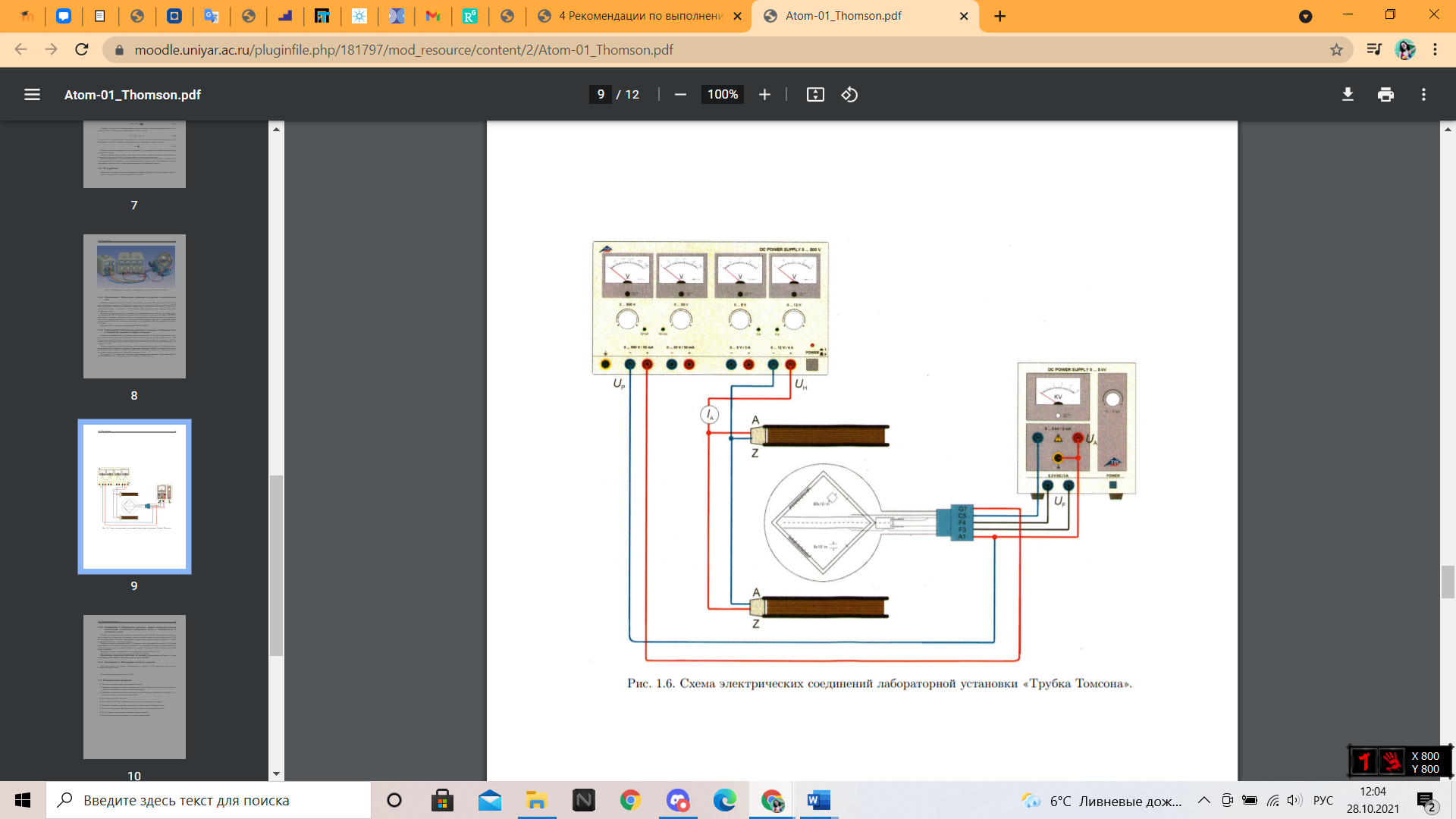
Рисунок 6 - Схема электрических соединений лабораторной установки «Трубка Томсона».
Упражнение 1.
Значения отклонений электронного пучка при напряжении на аноде 2000В, 3000В и 4000В. Отклонение происходит благодаря электрическому полю воздушного конденсатора.
Таблица 1 – Экспериментальные данные отклонения электронного пучка в электрическом поле при различных напряжения на аноде (g – отклонение пучка электронов)
При Uа = 2000В |
При Uа = 3000В |
При Uа = 4000В |
|||
Uк, В |
, мм |
Uк, В |
, мм |
Uк, В |
, мм |
160 |
16 |
200 |
14 |
180 |
12 |
180 |
18 |
220 |
16 |
260 |
14 |
260 |
20 |
300 |
18 |
320 |
16 |
300 |
22 |
350 |
19 |
|
|
350 |
24 |
|
|
|
|
Построим зависимость y от Uк.
Из уравнения (18) выразим. При
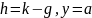 .
.
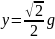
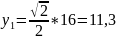
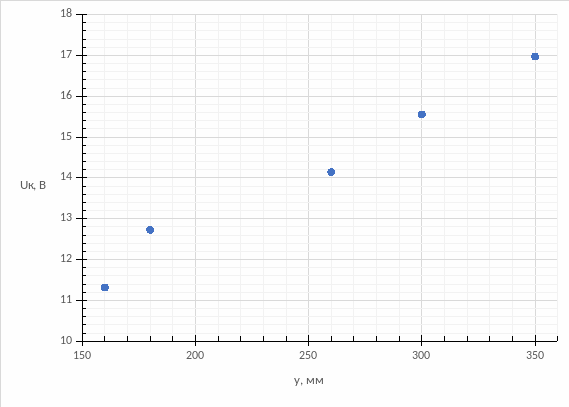
Рисунок 7 - Зависимость координаты y от напряжения на обкладках конденсатора Uк при напряжении на аноде Ua = 2000В
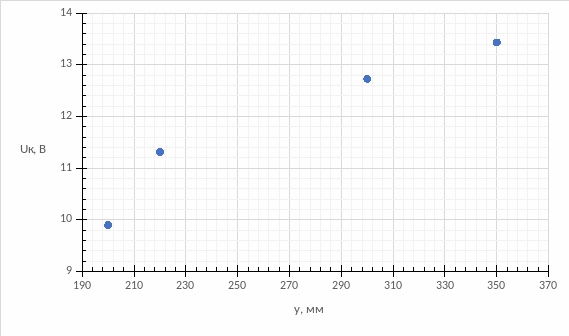
Рисунок 8 - Зависимость координаты y от напряжения на обкладках конденсатора Uк при напряжении на аноде Ua = 3000В
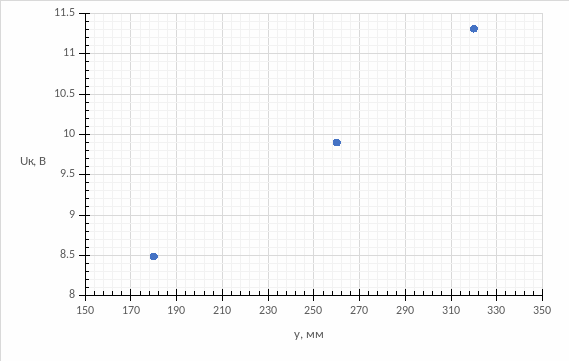
Рисунок 9 – Зависимость координаты y от напряжения на обкладках конденсатора Uк напряжении на аноде Ua = 4000В
Упражнение 2
Значения отклонений электронного пучка при напряжении на аноде 2000В, 3000В и 4000В. Отклонение происходит благодаря магнитному полю создаваемое катушками Гельмгольца.
Таблица 2 - Экспериментальные данные отклонения электронного пучка в магнитном поле при различных напряжения на аноде (g – отклонение пучка электронов)
Uа = 2000В |
Uа = 3000В |
Uа = 4000В |
|||||
Iг, А |
g, мм |
Iг, А |
g, мм |
Iг, А |
g, мм |
||
0,50 |
34 |
0,50 |
38 |
0,50 |
32 |
||
0,60 |
40 |
0,60 |
44 |
0,60 |
38 |
||
0,70 |
44 |
0,70 |
48 |
0,70 |
42 |
||
Формула расчёта удельного заряда электрона:
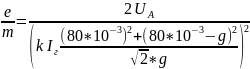
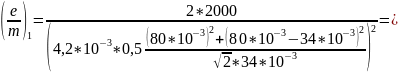
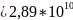
Таблица 3 – Рассчитанные значения удельного заряда электрона для эксперимента с магнитным полем
-
Uа, В
e/m, Кл/кг
2000
2,89E+10
3,15E+10
3,03E+10
3000
3,93E+10
4,12E+10
3,87E+10
4000
2,45E+10
2,73E+10
2,65E+10
Среднее значение.
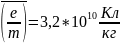
Погрешность измерений.
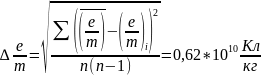
Относительная погрешность.
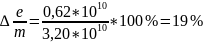
Упражнение 3
Для определения удельного заряда электрона замерим компенсационное напряжение на конденсаторе при определённом токе на катушках Гельмгольца чтобы отсутствовало отклонение электронного пучка.
Таблица 4 - Экспериментальные данные компенсации отклонения электронного пучка в магнитном и электромагнитном поле при различном напряжении на аноде
Uа = 2000 В |
Uа = 3000 В |
Uа = 4000 В |
||||
Iг, А |
Uк, В |
Iг, А |
Uк, В |
Iг, А |
Uк, В |
|
0,50 |
200 |
0,50 |
280 |
0,50 |
320 |
|
0,60 |
240 |
0,60 |
320 |
0,60 |
- |
|
0,70 |
280 |
0,70 |
360 |
0,70 |
- |
|
По формуле (22) рассчитаем удельный заряд электрона для каждого опыта.

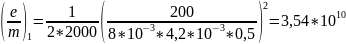
Таблица 5 – Рассчитанные значения удельного заряда электрона для эксперимента с компенсацией магнитного и электрического поля для различных напряжений на аноде
-
Uа, В
e/m, Кл/кг
2000
3,54E+10
3,54E+10
3,54E+10
3000
4,63E+10
4,20E+10
3,90E+10
4000
4,54E+10
Среднее значение.
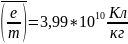
Погрешность измерений.
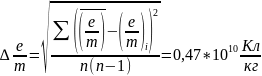
Относительная погрешность.
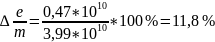
Упражнение 4
Поданным полученным в упражнение 3 и формуле (1.23) рассчитаем скорости электронов для каждого эксперимента.
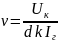
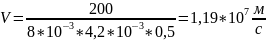
Таблица 6 – Рассчитанные значения скорости электронов при различных напряжениях на аноде
-
Uа, В
V, м/с
2000
1,19E+07
1,19E+07
1,19E+07
3000
1,67E+07
1,59E+07
1,53E+07
4000
1,90E+07
Вывод
Рассмотрев каждый из способов отклонения пучка и рассчитав удельный заряд электрона получили такие результаты.
Для опыта с воздушным конденсатором
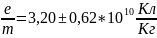
Для опыта с катушками Гельмгольца.
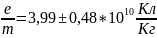
А также получили скорость электронов в пучке. В ходе лабораторной работы было изучено движение электрона в электрическом и магнитном полях и был определён удельный заряд электрона. Данный метод определения удельного заряда электрона показал низкую точность. Так как табличное значение удельного заряда электрона равно
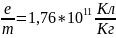
Для сравнения с табличными значениями. Рассмотри расхождение в процентах. Для первого опыта.
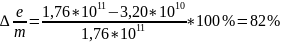
Для второго опыта.
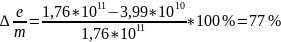
Можно сделать вывод, что в формулах для нахождения удельного заряда электрона не хватает коэффициента примерно равного 4.
Список литературы.
1.Алексеев, В.П. Лабораторная работа №1 / В.П. Алексеев, Е.О. Неменко – 10 с.
