Лабы по электричеству 2020 / ЛАБ6
.docxЛабораторная работа №6
ИЗУЧЕНИЕ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
Цель работы: экспериментальное исследование электростатического поля в области между заряженными электродами различной конфигурации и описание его при помощи эквипотенциальных поверхностей и силовых линий.
Приборы и принадлежности: стенд ЮУрГУ, соединительные провода.
Краткая теория.
1. Электростатическое поле. Напряженность поля.
Электростатическое
поле представляет собой частный случай
электромагнитного поля и создается
неподвижными электрическими зарядами.
Электростатическое
поле
в
каждой точке характеризуется значениями
напряженности
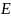 и
потенциала
и
потенциала
 ,
которые
являются силовой и энергетической
характеристиками поля в данной точке.
,
которые
являются силовой и энергетической
характеристиками поля в данной точке.
Действие
электростатического поля проявляется
в том, что помещенный в какую-либо точку
пространства пробный заряд
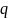 оказывается
под действием некоторой силы
оказывается
под действием некоторой силы
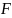 со стороны поля. За напряженность поля
принимается векторная величина, по
определению равная:
со стороны поля. За напряженность поля
принимается векторная величина, по
определению равная:
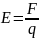 , (6.1)
, (6.1)
и характеризующая электрическое поле в данной точке. Согласно формуле (1) напряженность электрического поля численно равна отношению силы, действующей на помещенный в данную точку поля точечный заряд, к величине этого заряда, а направление вектора совпадает с направлением силы, действующей на положительный заряд.
Напряженность поля, созданного точечным зарядом в вакууме, как следует из закона Кулона, в системе "СИ" определяется формулой:
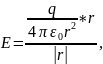 (6.2)
(6.2)
где
ε0
- электрическая постоянная, равная
8,85·10-12
Ф/м, r
- расстояние от заряда до данной точки,
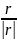 - единичный вектор, направленный от
заряда к данной точке.
- единичный вектор, направленный от
заряда к данной точке.
Для электрического поля справедлив принцип суперпозиции:
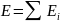 (6.3)
(6.3)
где
- напряженность поля системы зарядов,
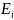 - напряженность
поля, создаваемого отдельным зарядом.
- напряженность
поля, создаваемого отдельным зарядом.
Таким образом, электрическое поле можно описать, указав для каждой точки пространства величину и направление вектора напряженности . Совокупность этих векторов образует некоторое векторное поле. Силовые линии или линии вектора напряженности проводят так, что касательные к ним в каждой точке совпадают с направлением вектора в этой точке, а количество линий, пронизывающих единицу поверхности перпендикулярной направлению вектора численно равно значению .
2. Потенциал.
Так как силы, действующие между зарядами, являются центральными, а поле центральных сил консервативно, можно наряду с напряженностью поля ввести для описания поля величину , называемую потенциалом. Потенциал данной точки поля есть скалярная физическая величина, численно равная работе, которую совершает поле при перемещении единичного положительного заряда из данной точки поля в бесконечно удаленную, потенциал которой принимают за нуль:
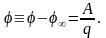 (6.4)
(6.4)
Работа по перемещению заряда q из точки с потенциалом φ1 в точку с потенциалом φ2 будет равна q (φ1 - φ2).
Связь напряженности электрического поля и потенциала определяется выражением:
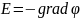 (6.5)
(6.5)
Знак минус в формуле показывает, что вектор напряженности поля направлен в сторону, противоположную вектору градиента потенциала
При графическом изображении электрического поля наряду с силовыми линиями поля используются эквипотенциальные поверхности, которые получаются, если соединить все точки, обладающие одним и тем же потенциалом. Силовые линии ортогональны эквипотенциальным поверхностям. В случае равномерно заряженной сферы, эквипотенциальные поверхности будут сферами, а силовые линии направлены по радиусам этих сфер. Электрическое поле, созданное между положительным зарядом и проводящей поверхностью показано на рис.1. Примеры изображения других электростатических полей при различной конфигурации электродов можно найти в учебниках.
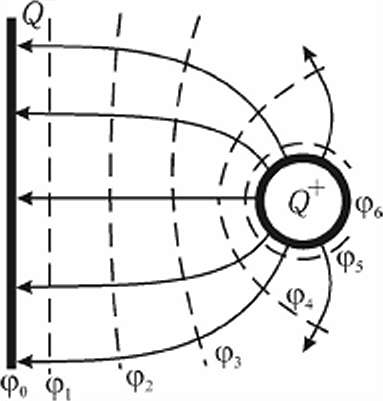
рис. 1. Силовые линии и эквипотенциальные поверхности для электростатического поля между положительным зарядом
и проводящей поверхностью.
Исходя из свойств взаимной ортогональности силовых линий и эквипотенциальных поверхностей, можно по силовым линиям поля найти поверхности равного потенциала, и, наоборот, по положению эквипотенциальных поверхностей можно построить силовые линии поля. Если перемещать заряд вдоль любого направления по эквипотенциальной поверхности, то работа будет равна нулю.
3. Метод исследования поля.
При конструировании многих электронных приборов требуется изучение электростатического поля в пространстве, заключенном между электродами. Изучить поле — это значит определить в каждой его точке значения и . Теоретический расчет и возможен лишь в случае полей, создаваемых электродами простой конфигурации. Сложные электростатические поля исследуют экспериментально.
Для изучения полей используют экспериментальные методы их моделирования. Один из них основан на применении слабо проводящей пластины с электродами. Электростатическое поле заменяют электрическим полем, в котором на электроды подают такие же потенциалы, как и в моделируемом поле. Несмотря на движение заряженных частиц, плотность зарядов на электродах постоянна, так как на место зарядов, уходящих по слабо проводящей пластинке, непрерывно поступают новые. Поэтому заряды электродов создают в пространстве такое же электрическое поле, как и неподвижные заряды той же плотности, а электроды являются эквипотенциальными поверхностями. Использование пластины позволяет применять токоизмерительные приборы, более простые и надежные в работе, чем электростатические.
При исследовании поля снимаем карту распределения потенциала, используя для измерения метод зонда. Электрический зонд представляет собой остроконечный проводник, который помещают в ту точку, где нужно измерить потенциал. В проводящей среде потенциал зонда равен потенциалу исследуемой точки поля.
Полученная картина эквипотенциальных поверхностей исследуемого поля позволяет провести силовые линии и вычислить значение модуля напряженности в любой точке. Вычисления усредненного значения напряженности на участке длины ∆n выполняются по формуле (6.6):
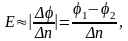 (6.6)
(6.6)
где
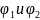 - потенциалы соседних эквипотенциальных
поверхностей,
- потенциалы соседних эквипотенциальных
поверхностей,
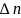 - кратчайшее расстояние между ними (по
нормали).
- кратчайшее расстояние между ними (по
нормали).
Ход работы.
1. Я собрала электрическую схему, показанную на рис. 2, подключив входы блока моделирования полей согласно рис. 3
|
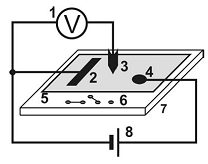
|
рис. 2. Электрическая схема. 1 – стрелочный вольтметр; 2,4 - электроды; 3 – зонд; 5 - пластина; 6- входы для подключения блока моделирования полей (рис. 4); 7 - блок моделирования полей; 8 -источник постоянного напряжения «0...+15 В» |
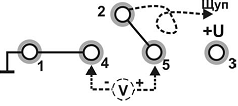
рис. 3. Входы для подключения блока моделирования полей: 1,3 — входы для подключения источника постоянного напряжения «О.…+15 В»; 2 - вход для подключения зонда; 4, 5 - входы для подключения стрелочного вольтметра |
2. Включила кнопкой «Сеть» питание блока генераторов напряжения. Нажала кнопку «Исходная установка».
3.
Касаясь
электродов зондом, определила, какой
электрод имеет нулевой потенциал
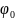 (левый).
(левый).
4.
Кнопками
установки напряжения
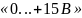 установила
потенциал другого электрода
установила
потенциал другого электрода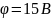 ,
контролируя его вольтметром (мультиметром).
,
контролируя его вольтметром (мультиметром).
5. Помещая зонд в центр каждой клетки на пластине, сняла карту распределения потенциалов. Результаты записала в виде таблицы:

Наглядные 3D модели (вид с боку и сверху).

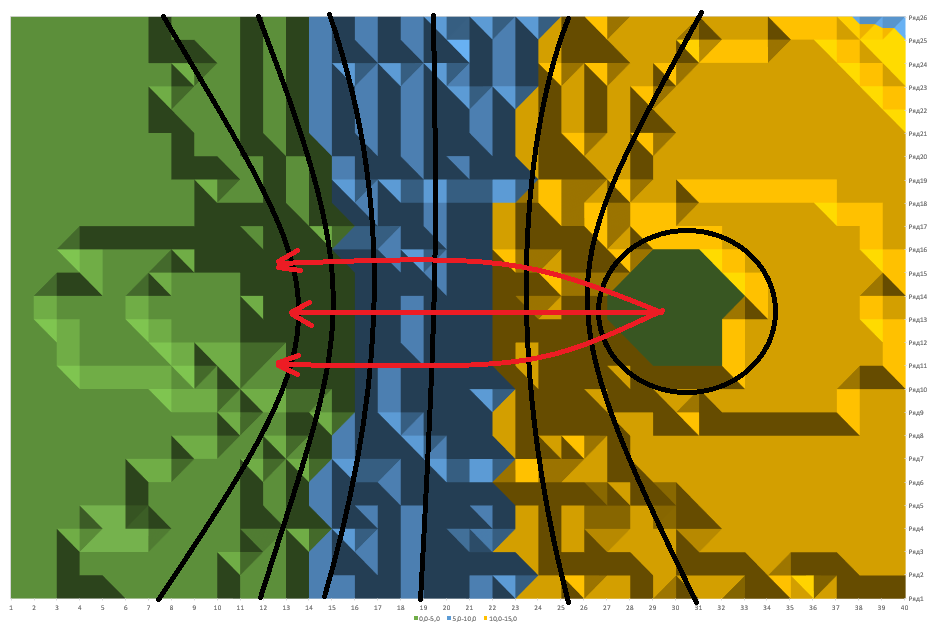
Вывод.
В ходе лабораторной работы мы исследовала электростатическое поле, разместив два разноименно заряженных электрода на слабо проводящей пластинке. Из таблицы видно, что максимальный потенциал имеет электрод, заряженный положительно. Линии напряженности электростатического поля всегда выходят из области более высокого потенциала, входят в области более низкого, соединяя разноименно заряженные электроды. Эквипотенциальные линии окружают электроды по окружности. Их выпуклость зависит от того, к какому заряду они ближе. В середине существует прямая эквипотенциальная линия. Так-же построил наглядные 3D модели.