РЭч1 / Домашние задания / ДЗ 1.2

№ 1.1

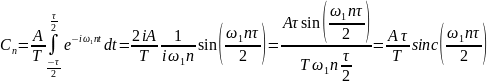
Огибающая спектра есть функция , зависящая непрерывно от 𝜔

Нули функции появляются тогда и только тогда, когда синк обращается в нуль

Sinc обращается в нуль при π, это и будет наш первый нуль и он равен скважности

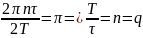
Sinc обращается в нуль при 2π, это будет наш второй нуль и он равен удвоенной скважности

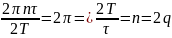
№ 1.2

Рассмотрим данный сигнал как непериодическую функцию

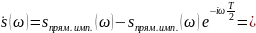
Переходим к комплексному спектру сигнала

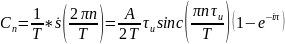
Сравним со спектром из № 1.1

№ 1.3

Нет, так как амплитудный спектр – это модуль спектральной плотности, а он всегда равен 1

№ 1.4

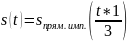
Т.к. спектр импульса в частотной области стал шире в три раза, то он сузился во временной области в три раза, а это приведёт к наложению двух соседних спектров импульсов друг на друга, что приведёт к тому что цепь некорректно будет обрабатывать входной сигнал.

№ 1.5

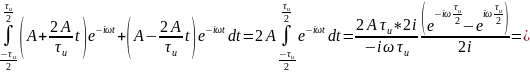
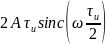
Функция обращается в ноль тогда, когда sinc обращается в ноль. Sinc равен нулю тогда, когда его аргумент равен π. Аргумент равен π при 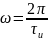. Получается, что ширина спектра, которую мы находим по первым двум нулям, равняется

№ 1.6

Функция обращается в ноль тогда, когда sinc обращается в ноль. Sinc равен нулю тогда, когда его аргумент равен π. Аргумент равен π при . Получается, что ширина спектра равняется

Функция обращается в ноль тогда, когда sinc обращается в ноль. Sinc равен нулю тогда, когда его аргумент равен π. Аргумент равен π при . Получается, что ширина спектра равняется

Из этого следует, что ширина спектра уменьшится в 2 раза.

№ 1.7

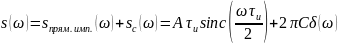
№ 1.8

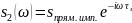
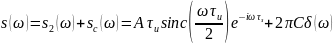
№ 1.9

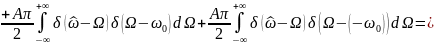
Физический спектр:

Данный спектр сопоставим со спектром сигма-функции на частоте 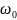. Что означает что огибающая сигнала совпала со спектром данного сигнала.

№ 1.10

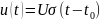
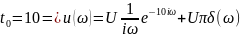
№ 1.11

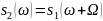
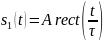
№ 1.12

№ 1.13

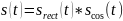
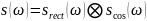
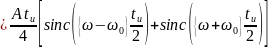
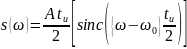
Найдём частоты, на которых заканчивается главный лепесток:

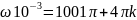
Полоса пропускания:

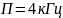
№ 1.14

Скорость звука – V, 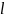– расстояние до объекта