34. Представление колебаний с помощью векторной диаграммы.

Векторная диаграмма — графическое изображение меняющихся по закону синуса (косинуса) величин и соотношений между ними при помощи направленных отрезков — векторов. Векторные диаграммы широко применяются в электротехнике, акустике, оптике, теории колебаний и так далее.X

Гармоническое (то есть синусоидальное) колебание может быть представлено графически в виде проекции на некоторую ось (обычно берут ось координат Оx) вектора, вращающегося с постоянной угловой скоростью ω. Длина вектора соответствует амплитуде, угол поворота относительно оси (Ox) — фазе.X

Сумма (или разность) двух и более колебаний на векторной диаграмме представлена при этом (геометрической) суммой^[1] (или разностью) векторов этих колебаний. Мгновенное значение искомой величины определяется при этом проекцией вектора суммы на ось Оx, амплитуда — длиной этого вектора, а фаза — углом его поворота относительно Ox.X

Н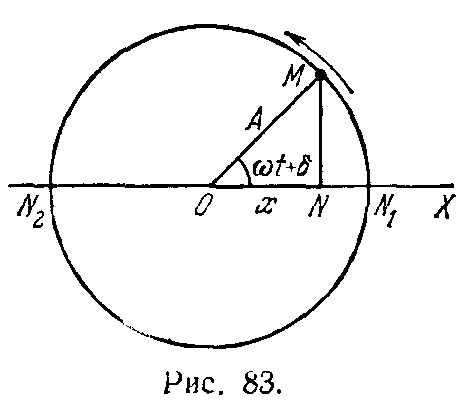 ачнем с колебательного движения материальной точки. В таком движении точка через равные промежутки времени проходит через одно и то же положение и притом в одном и том же направлении. Важнейшим среди колебательных движений является так называемое простое или гармоническое колебательное движение. Характер такого движения лучше всего раскрывается с помощью следующей кинематической модели. Допустим, что геометрическая точка М равномерно вращается по окружности радиуса А с постоянной угловой скоростью со (рис. 83). Ее проекция N на диаметр, например на ось X, будет совершать колебательное движение от крайнего положения N1 до другого крайнего положения N2 и обратно. Такое колебание точки N и называют простым или гармоническим колебанием. Чтобы его описать, надо найти координату х точки N как функцию времени t. Допустим, что в начальный момент времени t = 0 радиус ОМ образовывал с осью X угол б. Спустя время t этот угол получит приращение и сделается равным

Из рис. 83 видно, что

Эта формула и описывает аналитически гармоническое колебательное движение точки N вдоль диаметра Величина А дает максимальное отклонение колеблющейся

точки от положения равновесия О. Она называется амплитудой колебания. Величина называется циклической частотой. Величину

называют фазой колебания, а ее значение при t = 0, т. е.

величину б, — начальной фазой. Если б = 0, то х = A cos t;

если , то и т. д. Таким образом, при гармоническом колебании абсцисса х является синусоидальной или косинусоидальнои функцией времени t. Для графического изображения гармонического колебательного движения можно откладывать по горизонтальной оси время t, а по вертикальной оси — смещение точки х (рис. 22). Тогда получится периодическая кривая — синусоида. Форма кривой полностью определяется амплитудой А и циклической частотой . Однако ее положение зависит также от начальной фазы б. По истечении времени фаза получает приращение , а колеблющаяся точка возвращается в свое исходное положение с сохранением начального направления движения. Время Т называется периодом колебания. Скорость колеблющейся точки найдется дифференцированием

выражения по времени. Это дает

Дифференцируя вторично, получаем ускорение

или, используя ,

Сила, действующая на материальную точку при гармоническом колебании, равна.

Она пропорциональна отклонению х и имеет противоположное направление. Она всегда направлена к положению равновесия. Такого рода силы часто возникают при малых смещениях материальной точки из положения равновесия.