
- •Вопрос 30. Теорема Штейнера-Гюйгенса.
- •Вопрос 31. Момент сил, действующий на произвольную ось вращения.
- •Вопрос 32. Тензор инерции.
- •Вопрос 33. Колебания
- •34. Представление колебаний с помощью векторной диаграммы.
- •35. Сложение колебаний. Одномерный случай.
- •2. Два гармонических колебания x1 и x2 называются когерентными, если разность их фаз не зависит от времени:
- •4. Сложение сонаправленных колебаний с неравными, но близкими частотами.
- •36. Математический маятник.
- •37. Физический маятник.
- •38. Энергия колебаний. Средняя кинетическая и потенциальная энергия.
- •39. Гармонический осциллятор. Фазовая плоскость.
Вопрос 32. Тензор инерции.
Будем
считать, что тело состоит из отдельных
материальных точек с массами 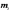 .
Закрепим тело в точке
.
Закрепим тело в точке 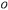 .
Пусть
.
Пусть 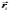 -
радиус-векторы точек
относительно
точки
-
радиус-векторы точек
относительно
точки  ,
а
,
а 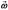 -
мгновенная угловая скорость тела, тогда
скорость
-
мгновенная угловая скорость тела, тогда
скорость 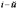 точки:
точки: 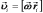 .
Момент импульса всего тела относительно
точки
.
Момент импульса всего тела относительно
точки  :
:
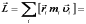
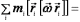
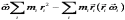 . (10.106)
. (10.106)
Рассмотрим
проекции на оси координат: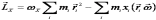 ;
;
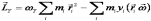 ;
; 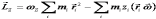 .(10.107)
.(10.107)
Учитывая,
что
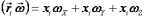 , (10.108)
, (10.108)
имеем: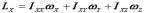 ;
;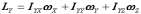 ;
;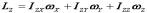 . (10.109)
. (10.109)
Здесь: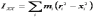 ;
; 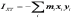 ;
; 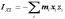 . (10.110)
. (10.110)
Очевидно,
что 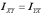 ;
; 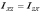 ;
; 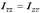 и
тд. Потому из 9 величин
и
тд. Потому из 9 величин 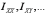 являются
различными лишь 6. Величины
являются
различными лишь 6. Величины 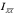 ,
,  ,
, 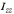 -
называются осевыми моментами инерции; а
величины
-
называются осевыми моментами инерции; а
величины 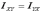 ,
, 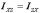 ,
, 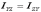 -
центробежными моментами инерции. Таким
образом, момент импульса весьма сложно
зависит от распределения масс в теле и
его направление, вообще говоря, не
совпадает с направлением угловой
скорости вращения тела. Поэтому в
общем случае нельзя писать
-
центробежными моментами инерции. Таким
образом, момент импульса весьма сложно
зависит от распределения масс в теле и
его направление, вообще говоря, не
совпадает с направлением угловой
скорости вращения тела. Поэтому в
общем случае нельзя писать 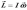 ,
а необходимо приводить уравнение для
проекций на соответствующую ось (ось
вращения). Совокупность величин
,
а необходимо приводить уравнение для
проекций на соответствующую ось (ось
вращения). Совокупность величин 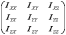 называются тензором инерции.
Величины
называются тензором инерции.
Величины 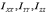 называются
диагональными элементами тензора, а
остальные – недиагональными элементами.
В данном случае элементы, расположенные
симметрично относительно диагонали,
равны. Такой тензор называется
симметричным.
называются
диагональными элементами тензора, а
остальные – недиагональными элементами.
В данном случае элементы, расположенные
симметрично относительно диагонали,
равны. Такой тензор называется
симметричным.
Первый закон Ньютона: всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит ее изменить это состояние. Те системы, по отношению к которым выполняется первый закон Ньютона, называются инерциальными системами отсчета.
Вопрос 33. Колебания
Процессы, повторяющиеся во времени называются колебаниями.
В
зависимости от природы колебательного
процесса и механизма возбуждения бывают:
механические колебания (колебания
маятников, струн, зданий, земной
поверхности и т.д.); электромагнитные
колебания (колебания переменного тока,
колебания векторов 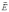 и
и 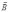 в
электромагнитной волне и т.д.);
электромеханические колебания (колебания
мембраны телефона, диффузора
громкоговорителя и др.); колебания ядер
и молекул в результате теплового движения
в атомах.
в
электромагнитной волне и т.д.);
электромеханические колебания (колебания
мембраны телефона, диффузора
громкоговорителя и др.); колебания ядер
и молекул в результате теплового движения
в атомах.
Рассмотрим отрезок [ОД] (радиус-вектор), совершающий вращательное движение вокруг точки 0. Длина |ОД| = A. Вращение происходит с постоянной угловой скоростью ω0. Тогда угол φ между радиус-вектором и осью x меняется со временем по закону
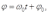
где φ0 - угол между [ОД] и осью х в момент времени t = 0. Проекция отрезка [ОД] на ось х в момент времени t = 0
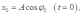
а в произвольный момент времени
 (1)
(1)
Таким образом, проекция отрезка [ОД] на ось х совершает колебания, происходящие вдоль оси х, и эти колебания описываются законом косинуса (формула (1)).
Колебания, которые описываются законом косинуса
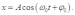
или синуса
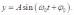
называется гармоническими.
Гармонические колебания являются периодическими, т.к. значение величины х (и у) повторяется через равные промежутки времени.
Промежуток времени, за который совершается одно полное колебание, называется периодом колебаний Т. Число колебаний в единицу времени называется частотой колебаний ν.
Промежуток времени, за который совершается одно полное колебание, называется периодом колебаний Т. Число колебаний в единицу времени называется частотой колебаний ν.
Свободными или собственными называются колебания, которые происходят в системе предоставленной самой себе после того, как она была выведена из положения равновесия или после того как ей был сообщен толчок.
Виды колебаний
Вынужденные — колебания, протекающие в системе под влиянием внешнего периодического воздействия. Примеры: листья на деревьях, поднятие и опускание руки. При вынужденных колебаниях может возникнуть явление резонанса: резкое возрастание амплитуды колебаний при совпадении собственной частоты осциллятора и частоты внешнего воздействия.
Свободные (или собственные) — это колебания в системе под действием внутренних сил после того, как система выведена из состояния равновесия (в реальных условиях свободные колебания всегда затухающие). Простейшими примерами свободных колебаний являются колебания груза, прикреплённого к пружине, или груза, подвешенного на нити.
Автоколебания — колебания, при которых система имеет запас потенциальной энергии, расходующейся на совершение колебаний (пример такой системы — механические часы). Характерным отличием автоколебаний от вынужденных колебаний является то, что их амплитуда определяется свойствами самой системы, а не начальными условиями.
Параметрические — колебания, возникающие при изменении какого-либо параметра колебательной системы в результате внешнего воздействия.
Случайные — колебания, при которых внешняя или параметрическая нагрузка является случайным процессом.
