
- •10. Закон сохранения импульса, проекции импульса.
- •13. Сила и потенциальная энергия. Градиент.
- •1 4. Кинетическая энергия материальной точки.
- •15. Полная механическая энергия материальной точки. Консервативные, неконсервативные силы.
- •16. Система частиц. Внутренние и внешние силы. Потенциальная энергия системы. Собственная энергия.
- •17. Полная энергия системы материальных точек. Закон сохранения энергии.
13. Сила и потенциальная энергия. Градиент.
Градиент (от лат. gradiens, род. падеж gradientis — шагающий) — характеристика, показывающая направление наискорейшего возрастания некоторой величины, значение которой меняется от одной точки пространства к другой. Например, если взять высоту поверхности Земли над уровнем моря (2-мерное пространство), то её градиент в каждой точке поверхности будет показывать «в горку».
Как видно из объяснения, градиент является векторной функцией, а величина, которую он характеризует — функцией скалярной.
Формально,
для случая трёхмерного пространства,
градиентом называется векторная функция
с компонентами  ,
, 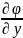 ,
,  ,
где φ — некоторая скалярная функция координат
x, y, z.
,
где φ — некоторая скалярная функция координат
x, y, z.
Если φ —
функция n переменных  ,
то её градиентом будет n-мерный вектор
,
то её градиентом будет n-мерный вектор![]() ,
компоненты которого равны частным
производным φ по всем её аргументам.
,
компоненты которого равны частным
производным φ по всем её аргументам.
Градиент
обозначается  или,
с использованием оператора
набла,
или,
с использованием оператора
набла, 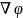 .
.
Из определения градиента следует, что:
![]()
В различных отраслях физики используется понятие градиента различных физических полей.
Например, градиент концентрации — нарастание или уменьшение по какому-либо направлению концентрации растворённого вещества, градиент температуры - увеличение или уменьшение по направлению температуры среды и т.д.. Градиент может быть вызван различными причинами, например, механическим препятствием, действием электромагнитных, гравитационных или других полей или различием в растворяющей способности граничащих фаз, например, октанол/вода.
Каждой точке
потенциального поля соответствует, с
одной стороны, некоторое значение
вектора силы
,
действующей на тело, и, с другой стороны,
некоторое значение потенциальной
энергии 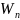 .
Следовательно, между силой и потенциальной
энергией должна существовать определенная
связь.
.
Следовательно, между силой и потенциальной
энергией должна существовать определенная
связь.
Д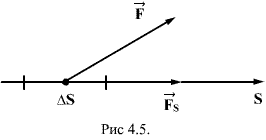 ля
установления этой связи вычислим
элементарную работу ∆A,
совершаемую силами поля при малом
перемещении ∆S
тела, происходящем вдоль произвольно
выбранного направления в пространстве,
которое обозначим буквой S.
Эта работа равна
ля
установления этой связи вычислим
элементарную работу ∆A,
совершаемую силами поля при малом
перемещении ∆S
тела, происходящем вдоль произвольно
выбранного направления в пространстве,
которое обозначим буквой S.
Эта работа равна
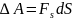
где  -
проекция силы
на
направление S.
-
проекция силы
на
направление S.
Поскольку в данном
случае работа совершается за счет запаса
потенциальной энергии
,
она равна убыли потенциальной энергии 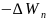 на
отрезке оси
на
отрезке оси 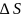 :
:

Из двух последних
выражений получаем
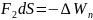 =>
=>

Последнее выражение дает среднее значение на отрезке ∆S. Чтобы
получить значение
в
точке нужно произвести предельный
переход:
![]()
Так как
может
изменяться не только при перемещении
вдоль оси S,
но также и при перемещениях вдоль других
направлений, предел в этой формул
представляет робой так называемую
частную производную от
по S:

Это соотношение
справедливо для любого направления в
пространстве, в частности и для направлений
декартовых координатных осей х, у, z:
![]()
Эта формула определяет проекции вектора силы на координатные оси. Если известны эти проекции, оказывается определенным и сам вектор силы:
![]() в математике вектор
в математике вектор ![]() ,
где a
- скалярная функция х, у, z, называется
градиентом этого скаляра обозначается
символом
,
где a
- скалярная функция х, у, z, называется
градиентом этого скаляра обозначается
символом 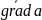 .Следовательно
сила равна градиенту потенциальной
энергии, взятого с обратным знаком
.Следовательно
сила равна градиенту потенциальной
энергии, взятого с обратным знаком


