11. Закон сохранения импульса, проекции импульса.

12. Работа, мощность силы.

13. Работа центральных сил. Консервативные силы. Потенциальная энергия.

14. Потенциальный барьер, потенциальная яма. Финитное, инфинитное движение.

15. Сила и потенциальная энергия. Градиент.

11. Закон сохранения импульса, проекции импульса.

 

      Рассмотрим систему состоящую из n материальных точек, взаимодействующих между собой.

 

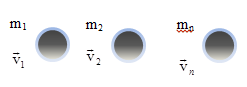
Силы взаимодействия между телами, образующими систему, обозначим 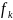. Взаимодействие внешних сил со стороны тел не входящих в данную систему на і-тое тело системы обозначим .

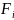       Запишем  ІІ закон Ньютона применительно ко всем телам, образующим систему:

 

по III закону Ньютона

 

   

      Векторная сумма импульсов всех тел, образующих данную систему называется результирующим импульсом системы.

      Если внешние силы не действуют на тела системы (нет взаимодействия между телами, входящими в систему и внешними телами), или действие внешних сил скомпенсирована, то система называется замкнутой или изолированной.

     В этом случае

   Закон сохранения импульса:

геометрическая (векторная) сумма импульсов замкнутой системы остаётся постоянной с течением времени при любых взаимодействиях внутри системы:

 

З. С. И.          

т. е. в результате взаимодействия между телами системы импульсы отдельных тел могут изменяться как по величине, так и по направлению, но в таких рамках, что векторная сумма импульсов всех тел, образующих данную систему остаётся величиной постоянной.

Пример 1: абсолютно упругий удар З.С.И:  .      =>

Проекция на ось x: 

Пример 2: Упругий удар шара об неподвижную стенку

 

 

                                                     

                                                            

 

 

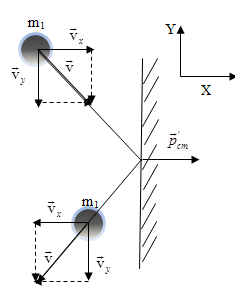
Билет 12. Работа, мощность силы.

Работой силы F на перемещение ds называется проекция F_s этой силы на направление перемещения, умноженная на само перемещение: .(1)

Где α – угол между векторам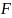и и 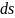(рис 36). Поскольку перемещение предполагается бесконечно малым, величина называется также элементарной работой в отличие от работы на конечном перемещении. Если воспользоваться понятием скалярного произведения, то можно сказать, что элементарная работа есть скалярное произведение силы на перемещение : 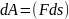(2). В общем случае, когда материальная точка, двигаясь по криволинейной траектории, проходит путь конечной длины, можно мысленно разбить этот путь на бесконечно малые элементы, на каждом из которых сила может считаться постоянной, а элементарная работа может быть вычислена по формуле (1) или (2). Если сложить все эти элементарные работы и перейти к пределу, устремив к нулю длины всех элементарных перемещений, а число их – к бесконечности, то такой предел обозначается символом 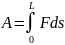и называется криволинейным интегралом вектора F вдоль траектории L. Этот интеграл, по определению, и дает работу силы F вдоль кривой L. 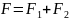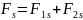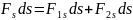Если , то проецируя это векторное уравнение на направление элементарного перемещения , получим , а после умножения : , или 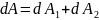. Таким образом, элементарная работа результирующей двух или нескольких сил равна сумме элементарных работ этих сил. Очевидно, то же утверждение справедливо и для работ на конечных перемещениях: 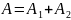. Единицей работы в системе СИ является Джоуль(Дж). Джоуль есть работа силы в один ньютон на перемещение в один метр при условии, что направление силы совпадает с направлением перемещения. В системе СГС единой единицей работы является эрг. Эрг есть работа силы в одну дину на перемещении в один сантиметр при том же условии, т.е. в предположении, что направления силы и перемещения совпадают. Очевидно, 1Дж=10⁷ эрг. Работа, отнесенная к единице времени, т.е. 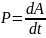величина , называется мощностью. Ее единицами являются эрг на секунду и джоуль на секунду, или ватт(Вт)Очевидно, 1Вт=10⁷эрг/с.