- •2 Билет:
- •4 Билет:
- •5 Билет: Согласно представлениям классической механики, механические явления происходят одинаково в двух системах отсчета, движущихся равномерно и прямолинейно относительно друг друга.
- •Выражение (8.1.3) определяет закон сложения скоростей в классической механике. Из него следует, что скорость движения точки м (сигнала) в системе k' и в системе k различна.
1. Физическая модель. Физические величины, их измерение. 2. Осн. понятия кинематики. Координатный и «естественный» способы описания движения. 3. Движение по окружности. Вектор угловой скорости. 4. Инерциальные системы отсчета. I закон Ньютона. 5. Принцип относительности Галилея. Преобразования Галилея. Сложение скоростей.
1 билет: Физическая модель - это модель, создаваемая путем замены объектов моделирующими устройствами, которые имитируют определённые характеристики либо свойства этих объектов. Простейшая физическая модель-объект, размерами которого можно пренебречь(материальная точка) Физическая величина-величина, характеризующая свойства физического мира и применяемая в физических науках.
Группы величин: 1)Свойства объектов(длина,масса) 2)Состояние системы(давление,температура) 3)Процессы(скорость,мощность)
Измерение-это экспериментальное сравнение одной измеряемой величины с другой известной величиной того же качества,принятой в качестве единицы. Для каждой физической величины приняты свои единицы. Для удобства все страны мира стремятся пользоваться одинаковыми единицами физических величин. Она применяется и в России – Международная система единиц – СИ (система интернациональная). Так, согласно этой системы основной единицей длины является – метр (1м), времени – секунда (1с), скорости – метр за секунду (1 м/с), массы – килограмм (1 кг). Единицы измерения-это физ. Величина фиксированного размера,которой условно присвоено числовое значение,равное единице и применяемое для количественного выражения однородных с ней физ.величин.
Измерение длины происходит непосредственно прямыми измерениями(прикладыванием принятого эталона к объекту) Измерение времени характеризуется измерением промежутка между двумя происходящими событиями.
2 Билет:
Материальная точка — объект, размерами которого в условиях данной задачи можно пренебречь, считая его массу сосредоточенной в одной точке пространства. Вектор — это направленный отрезок.
Траектория —
линия в пространстве, вдоль которой
движется материальная точка.
Путь —
это длина траектории.
Перемещение —
это вектор, соединяющий начальное и
конечное положение материальной точки
в пространстве.
Равномерное
движение —
движение с постоянной скоростью.
Уравнение равномерного движения  или
или  .
Средняя
скорость по перемещению —
векторная величина, равная отношению
перемещения ко времени
.
Средняя
скорость по перемещению —
векторная величина, равная отношению
перемещения ко времени
 Средняя
скорость по пути —
скалярная величина, равная отношению
пути (длины траектории) ко времени .
Средняя
скорость по пути —
скалярная величина, равная отношению
пути (длины траектории) ко времени .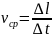 Мгновенная
скорость —
производная перемещения по времени .
Мгновенная
скорость —
производная перемещения по времени . При
равномерном движении мгновенная скорость
равна средней.
Ускорение —
это производная скорости по времени:
При
равномерном движении мгновенная скорость
равна средней.
Ускорение —
это производная скорости по времени:  .
При
криволинейном движении ускорение
материальной точки раскладывается на
две
составляющих: нормальное ускорение
.
При
криволинейном движении ускорение
материальной точки раскладывается на
две
составляющих: нормальное ускорение  и тангенциальное ускорение
и тангенциальное ускорение  :
:

 Составляющая
ускорения, направленная к центру кривизны
траектории, т.е. перпендикулярно
(нормально) скорости, называется
нормальным ускорением
Составляющая
ускорения, направленная к центру кривизны
траектории, т.е. перпендикулярно
(нормально) скорости, называется
нормальным ускорением
 .
Она характеризует изменение скорости
по направлению:
.
Она характеризует изменение скорости
по направлению:
Составляющая
ускорения, направленная вдоль скорости,
называется тангенциальным ускорением
 .
Она характеризует изменение скорости
по модулю.
.
Она характеризует изменение скорости
по модулю.

При
равнопеременном прямолинейном
движении ускорение
материальнaой
точки равно изменению ее скорости за
единицу времени (одну секунду):

 Уравнение,
выражающее зависимость координаты тела
от времени его движения, называется уравнением
движения.
При координатном способе задания
движения:
Уравнение,
выражающее зависимость координаты тела
от времени его движения, называется уравнением
движения.
При координатном способе задания
движения:
То есть и вектор скорости точки, и вектор ее ускорения при координатном способе задания движения определяются через их проекции на координатные оси
Естественный способ описания движения: когда заданы траектория точки и закон движения точки вдоль этой траектории в виде s = s(t).
В этом случае
векторы v и a определяют
по их проекциям не на оси системы
координат Oxyz, а на подвижные оси P![]() nb,
имеющие начало в точке Р и движущиеся
вместе с нею (см.рис.). Эти оси,
называемые осями
естественного трехгранника,
направлены следующим образом:
nb,
имеющие начало в точке Р и движущиеся
вместе с нею (см.рис.). Эти оси,
называемые осями
естественного трехгранника,
направлены следующим образом:
ось P направлена по касательной к траектории в сторону положительного направления отсчета координаты s;
ось Pn направлена по нормали к траектории, лежащей в соприкасающейся плоскости и направленной в сторону вогнутости траектории;
ось Pb направлена перпендикулярно к первым двум осям P и Pn так, чтобы она образовалаправую систему осей (с положительного направления оси Pb поворот оси P к оси Pn в их плоскости на прямой угол виден происходящим против хода часовой стрелки).
Нормаль Pn, лежащая в соприкасающейся плоскости (в плоскости самой кривой, если кривая плоская),называется главной нормалью, а перпендикулярная ей нормаль Pb - бинормалью. 3 билет:
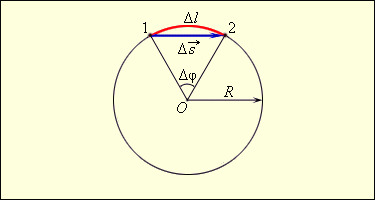
Движение
тела по окружности является
частным случаем криволинейного движения.
Наряду с вектором перемещения ∆ удобно
рассматривать угловое
перемещение Δφ(или угол
поворота),
измеряемое в радианах (рис. 1.6.1).
Длина дуги связана с углом поворота
соотношением
удобно
рассматривать угловое
перемещение Δφ(или угол
поворота),
измеряемое в радианах (рис. 1.6.1).
Длина дуги связана с углом поворота
соотношением 
При малых углах поворота Δl ≈ Δs.
|
|
Угловой
скоростью ω тела
в данной точке круговой траектории
называют предел ( )
отношения малого углового перемещения Δφ к
малому промежутку времени Δt:
)
отношения малого углового перемещения Δφ к
малому промежутку времени Δt: 
|
Угловая скорость измеряется в рад/с.
Связь между
модулем линейной скорости υ и
угловой скоростью ω: 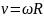
При равномерном
движении тела по окружности
величины υ и ω остаются
неизменными. В этом случае при движении
изменяется только направление вектора 
Равномерное
движение тела по окружности является
движением с ускорением.
 Ускорение
Ускорение
|
направлено
по радиусу к центру окружности. Его
называют нормальным или центростремительным
ускорением.
Модуль центростремительного ускорения
связан с линейной υ и угловой ω скоростями
соотношениями:  При
малых углах Δφ направление
вектора
При
малых углах Δφ направление
вектора  приближается
к направлению на центр окружности.
Следовательно, переходя к пределу
при Δt → 0,
получим:
приближается
к направлению на центр окружности.
Следовательно, переходя к пределу
при Δt → 0,
получим: 
При изменении положения тела на окружности изменяется направление на центр окружности. При равномерном движении тела по окружности модуль ускорения остается неизменным, но направление вектора ускорения изменяется со временем. Вектор ускорения в любой точке окружности направлен к ее центру. Поэтому ускорение при равномерном движении тела по окружности называется центростремительным.
Вектор угловой скорости: угловую скорость как вектор, величина которого численно равна угловой скорости, и направленный вдоль оси вращения, причем, если смотреть с конца этого вектора, то вращение направлено против часовой стрелки
Тогда
положение произвольной точки A задается
радиус-вектором r,
соединяющим начало отсчета с выбранной
точкой. Модуль скорости этой точки можно
рассчитать по формуле
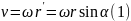 где
где  −
расстояние до оси вращения, α −
угол между векторами ω и r.
Направлен вектор скорости V перпендикулярно
плоскости, проходящей через векторы ω и r.
Так давайте, определим новую математическую
операцию над векторами ω и r,
такую, чтобы ее результатом был
вектор V.
Естественно,
что такая операция была придумана до
нас и называется она векторным
произведением
−
расстояние до оси вращения, α −
угол между векторами ω и r.
Направлен вектор скорости V перпендикулярно
плоскости, проходящей через векторы ω и r.
Так давайте, определим новую математическую
операцию над векторами ω и r,
такую, чтобы ее результатом был
вектор V.
Естественно,
что такая операция была придумана до
нас и называется она векторным
произведением