Добавил:

Vor_fleshek Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МЭИ»

Предмет:

Моделирование систем управления

Файл:

MSU_Lektsii_Eliseev

.pdf

Скачиваний:

Добавлен:

26.01.2024

Размер:

2.64 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 143 4 5 6 7 8 9 10 11 12 13 14 > Следующая >>>

Моделирование систем управления

d n

d n 1

d n

d n 1

n 1

y b

n 1

Представим данное дифференциальное уравнение в виде следующей аналоговой схемы:

n		n-1		0

…

Будем искать значения коэффициентов i и i .

y x 1 0 u

x k	x k 1 k u ,
x k	x k 1 k u ,		k 1, n 1
	n	n u
x n i 1 x i		n u

i 1

Запишем значения всех n производных y:

y x 1 0 u x 2 1 u 0 u

y x 2 1 u

0 u x 3 2 u

1 u

0 u

( k )

x k

k i u

( i )

x k 1

k i u

( i )

1, n 1

i 1

i 0

( n )

x n

n i u

( i )

i 1

Подставляем:

y ( n ) i 1 x i

n u n i u ( i ) i 1 x i

n i u ( i )

i 1

i 0

Моделирование систем управления

Сравниваем с исходным дифференциальным уравнением:

n 1

( i )

( n )

a k y

( k )

bi u

( i )

a k

k i u

bi u

( i )

x k 1

k 0

i 0

k 0

i 0

n 1

y ( n ) a k 1 x k

a k k i u ( i ) bi u ( i )

k 1

k 0

i 0

Видим, что i a i , а i получаются в результате решения некоторой СЛУ:

Возьмем для простоты случай n=2:

				n
Из дифференциального уравнения следует:				n i u ( i )		2 u 1 u
				i 0
			n		n 1	k
Из полученного выражения y ( n )		имеем: bi u ( i )			a k k i u ( i )
			i 0		k 0	i 0
		1 u
или b 0 u b1 u	b 2 u a 0 ( 0 u ) a 1 (	1 u	0 u )

При соответствующих производных u имеем:

0 u

2	1	k
bi u ( i )	a k k i u ( i )
i 0	k 0	i	0

u :	0	b 2

u :	1	b1 a 1 0

u :	2	b 0 a 0 0 a 1 1

Или в матричной форме:

b 2	1	0	0 0

b1	a 1	1	0 1
		a 1		2
b 0	a 0	a 1	1	2

В общем случае для вычисления i следует решить такую СЛУ:

	b n

b n 1
b		n 2



	b 0

		1		0		0		0

a n 1				1	0		1
a		n 2	a	n 1	1				2
		n 2		n 1					2
						0
	a 0		a 1		a 2
	a 0		a 1		a 2	1		n

Что нам дает аналоговая структурная модель? Возможность как аппаратной (электронной), так и программной реализации.

Моделирование систем управления

Лекция 5. Получение уравнений в пространстве состояний

Способы получения моделей описания систем в векторно-матричной форме и преобразования к пространству состояний. Стандартная форма описания на основе структурной модели. Получение модели описания нормальной форме на основе решения характеристического уравнения (случай простых и кратных корней).

1.Метод разложения на простые дроби (канонические формы).

Можем рассматривать обобщенное управляющее воздействие u1=M(p)u. Далее без потери общности можем говорить о системе G(p)=1/L(p). Полагая, что L(p) имеет простые нули,

можно записать: L ( p ) ( p i ) , где i – корни

i 1

Разлагая 1/L(p) на простые дроби, получим:

L ( p )

полинома L(p) и полюсы G(p).

n		c i
		c i	, где ci – вычеты.
		p i	, где ci – вычеты.
i	1	p i

y ( t )

u ( t )

i 1

p i

Вводим обозначения: x i

( t )

u ( t ) , тогда y ( t )

c i x i

( t ) .

p i

i 1

Согласно предыдущему уравнению x i i x i

u ( t ) . Таким образом, матричное уравнение

системы в пространстве состояний имеет вид

Ax bu

, где A - диагональная матрица с

корнями полинома L(p) на диагонали, а b=(1 1 1 … 1)T .

Структурная схема:

Особенности канонической формы представления:

Матрица состояния диагональная с собственными числами на диагонали

Полюсы системы – собственные числа – фигурируют в явном виде

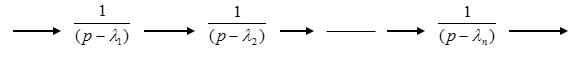
Моделирование систем управления

Если имеются комплексные корни, то они – комплексно-сопряженные. Применение данной формы представления неудобно, так как теряется возможность представлять состояние системы в n-мерном пространстве действительных чисел.

В	общем случае для кратных корней L ( p ) ( p	1	) k 1 ( p	i	) k i	( p	n	) k r , где
	r
n	k i

i 1

При этом матрица A приобретает нормальную жорданову форму:

	J k	1	( 1 )			0					i		1		0
			J k 2 ( 2 )										i				1,		j	k i
														1			1,		j	k i
														1						i 1
A									,	J k i ( i )						, b j				i 1
A									,	J k i ( i )					1	, b j
															1			0	j k i
																		0	j k i
			0	J k		( k		)				0
			0	J k	r	( k	r	)				0				i				i 1
					r		r									i

Уравнения состояния, матрица которых имеет нормальную жорданову форму, называются каноническими уравнениями состояния.

Если числитель M(p) передаточной функции имеет порядок меньший или равный порядку L(p), то система по-прежнему может быть описана теми же уравнениями. В случае равных порядков числителя и знаменателя в разложении появится постоянный член:

M ( p )

c i

c 0

L ( p )

i 1

где c 0

M ( p )

( p k

M ( p )

, k

lim

c k

)

1, n

L ( p )

p 0 L ( p )

p k

2. Метод простых множителей.

Если функция G(p) разложима на множители, то её можно представить в виде:

n		1
G ( p )		1

		( p i )
i	1	( p i )

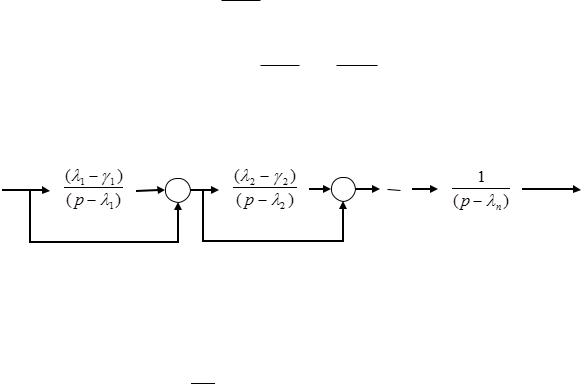
Соответствующая блок-схема:

u		x1		x2		y=xn

Моделирование систем управления											© 2016, В.Л. Елисеев
1			0						0
						1			0
	1 2
A	1			, b	0		,	c
										0

						0				1
						0				1
	0	1	n

Этот метод представления не ограничен случаем простых корней.

Если числитель M(p) передаточной функции имеет порядок меньший или равный порядку L(p), то система раскладывается на множители в соответствии с уравнением:

G ( p ) M ( p )

L ( p )

где i – корни полинома M(p). Так как

p i

( p i	)	n		1

( p i				i )
	) i l 1		( p

1 i i , то передаточную функцию

p i

можно реализовать следующей схемой:

y=kxn

Уравнения, описывающие поведение системы принимают вид:

dx 2

dx 1		x		(			) u
	1		1		1	1
dt

2 x 2 ( 2 2 ) x1 ( 2 2 ) u


dx n		x		x
	n	x	n	x	n 1
dt	n		n		n 1
dt

y kx n

3. Метод, применяемый при аналоговом моделировании.

При аналоговом моделировании система G(p)=1/L(p) реализуется с помощью сумматоров, инверторов-усилителей и идеальных интегрирующих элементов.

Пример:	G ( p )	1

		p 3 ap 2	bp	c
		p 3 ap 2	bp	c

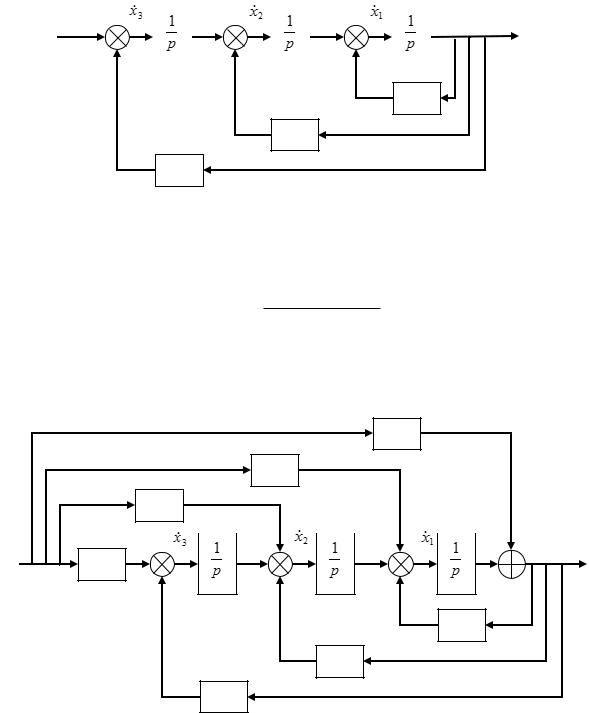
Можно записать уравнения состояния следующего вида:

x 1 x 2 ax 1

Моделирование систем управления

x 2 x 3 bx 1 x 3 cx 1 u y x 1

Блок-схема аналогового моделирования данной системы:

u	x3	x2	y=x1
u	x3	x2	y=x1

-b

-c

Пример реализации аналогового моделирования в случае если числитель M(p) передаточной функции имеет порядок меньший или равный порядку L(p):

G ( p )

dp 3 ep 2 fp g

p 3 ap 2 bp c

Можно увидеть, что влияние числителя обеспечивается соответствующими прямыми связями:

u		x3		x2		x1	y

-a

-b

-c

В матричной форме это выражается уравнениями:

Моделирование систем управления

	x 1
	x 2
	x 2

	x 3
	x 3

a		1	0 x 1			e ad

b		0	1 x 2		f bd			u
	c						g cd
	c	0	0	x 3			g cd

	x 1

y 1 0	0 x 2		du
		x 3
		x 3

На примере видно, что матрицы A и c не отличаются от случая G(p)=1/L(p).

Нормальная форма.

Классическим подходом при построении модели в пространстве состояний является использование в качестве переменных состояния выходного сигнала и его n-1 производных. Такая форма представления называется нормальной и отличается простотой, если собственные значения различны. Данную форму представления можно применять для нелинейных дифференциальных уравнений общего вида.

Выбирая

для

L ( p )

a n i

p i

качестве переменных состояния x 1 y ,

x 2

x 1 ,…,

x n 1 ,

получим

i 0

уравнения

состояния следующие матрицы

вектора

x n

для

коэффициентов:

, c

n 1

a 0

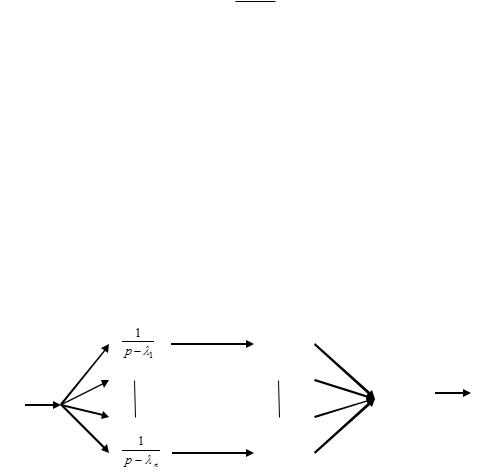
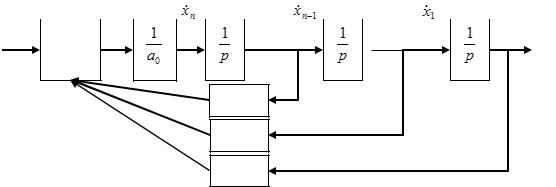
Аналоговая структурная схема:

xn-1

y=x1

-a1

-an-1

-an

Нормальная форма разложения при прямолинейном подходе в случае G(p)=M(p)/L(p) приводит к появлению производных от возмущающего воздействия u(t). Однако

Моделирование систем управления

специальной подстановкой можно устранить необходимость во взятии производных от u(t), сохранив вид нормальной формы.

Например, для

G ( p )

p a

дифференциальное уравнение

имеет вид

( p b )( p c )

y ( b c ) y bcy

u au

Подстановка вида

y x 1

k 0 u ,

x 1 x 2

k 1 u ,

x 2 bcx 1 ( b c ) x 2 k 2 u (*)

позволяет

выразить x1 и x2 через y и u:

x 1 y k 0 u ,						x	1	y k	0 u

x 2	x	1	k 1 u y k	0 u k	1 u	x	2	y k	0 u k	1 u

И, подставив выражения для x1 , x 2 , x1 , x 2					в (*), переписать дифференциальное уравнение
следующим образом:
	y k	0 u k 1 u bc ( y k 0 u ) ( b c ) y k				0 u k 1 u k 2 u

	y ( b c ) y		bcy k 0 u k	1	( b c ) k 0 u k 2	( b c ) k 1 bck	0 u

Отсюда: k 0	0 , k 1 1 , k 2		a ( b c )

Итоговое представление уравнений в пространстве состояний:

x 1

( b

x 2

c )

k 2

Для общего случая G(p)=M(p)/L(p) имеем:

n		n
L ( p ) a n i p i	,	M ( p ) b n j p j
i 0		j 0
Причем полином L(p) нормирован, т.е. a 0	1

Тогда можно показать, что в матричной форме уравнения состояния

x A bu

y c T x du

матриц A и вектора b, c имеют вид:

Моделирование систем управления													© 2016, В.Л. Елисеев
	0	1		0			k 1				1
	0	0	1
A	0	0	1			, b				, c	0	, d	k
A				1		, b	k			, c		, d	k
				1			k						0
													0
									n 1
	a n	a n 1		a				k n			0
	a n	a n 1		a	1			k n			0

Выходной сигнал y	x 1 k 0 u , а коэффициенты равны:
		i 1
	k 0 b 0 ,	k i bi a i m k m	, i 1, n

m 0

Моделирование систем управления

Лекция 6. Матричная форма представления

Приведение нормальной формы описания динамической системы к канонической форме путём линейного преобразования на основе матрицы подобия. Пример канонизации уравнений состояния. Способ получения уравнений состояния на основе структурной блок-схемы многосвязной динамической системы.

Преобразование из нормальной формы представления системы в каноническую

Описание динамической системы в пространстве состояний:

x Ax Bu

y Cx Du

Внормальной форме элементами вектора состояния x являются выходной сигнал и его первые n-1 производных.

Вканонической форме координаты x представляют собой составляющие собственных колебаний.

Мы видели, что в нормальной форме описания односвязной динамической системы матрицы имеют вид:

	0	1	0	0		1
						1		1
	0	0	1	0		2
								0
A					B		C	0	D	0




	0	0	0	1
						n		0
	a 0	a 1	a 2			n		0
	a 0	a 1	a 2	a n 1

где значения

	b n				1

b n 1			a n 1
b		n 2	a		n 2
		n 2			n 2

	b 0			a 0
	b 0			a 0

k , k	0 , n
0
1	0
a n 1	1
a 1	a 2

получаются в результате решения следующей СЛУ:

0	0

	1
		2
		2
0
1		n
1		n

Поскольку при преобразовании из нормальной формы в каноническую меняются переменные состояния x x * , обозначим этот переход линейным оператором – умножением на матрицу: x Vx *

Подставим:

V x *		AVx	* Bu	x *	V 1 AVx	* V 1 Bu
	y	CVx	* Du		y CVx	* Du

<<< < Предыдущая 1 23 / 143 4 5 6 7 8 9 10 11 12 13 14 > Следующая >>>

Соседние файлы в предмете Моделирование систем управления

#
26.01.20242.64 Mб12MSU_Lektsii_Eliseev.pdf
#
26.01.202414.56 Mб39MSU_lektsii_obedinenny.pdf
#
26.01.2024164.01 Кб14Демо-задачи по МСУ-2023.pdf
#
26.01.202413.46 Кб2Типы задач.docx
#
26.01.202418.98 Кб2Экз вопросы МСУ_2023 (1).docx