
Дашин_ЛБ2
.docxФедеральное государственное бюджетное образовательное учреждение высшего образования. «Национально исследовательский университет
«Московский энергетический институт»
Кафедра Управления и интеллектуальных технологий
Лабораторная работа №2
ИЗУЧЕНИЕ МЕТОДОВ ВИЗУАЛИЗАЦИИ И КЛАСТЕРИЗАЦИИ ДАННЫХ
Выполнил:
Дашин И.Н.
А-02-20
Москва 2022 г.
Проведем визуализацию данных в трехмерном пространстве для датасета «ирисы Фишера».
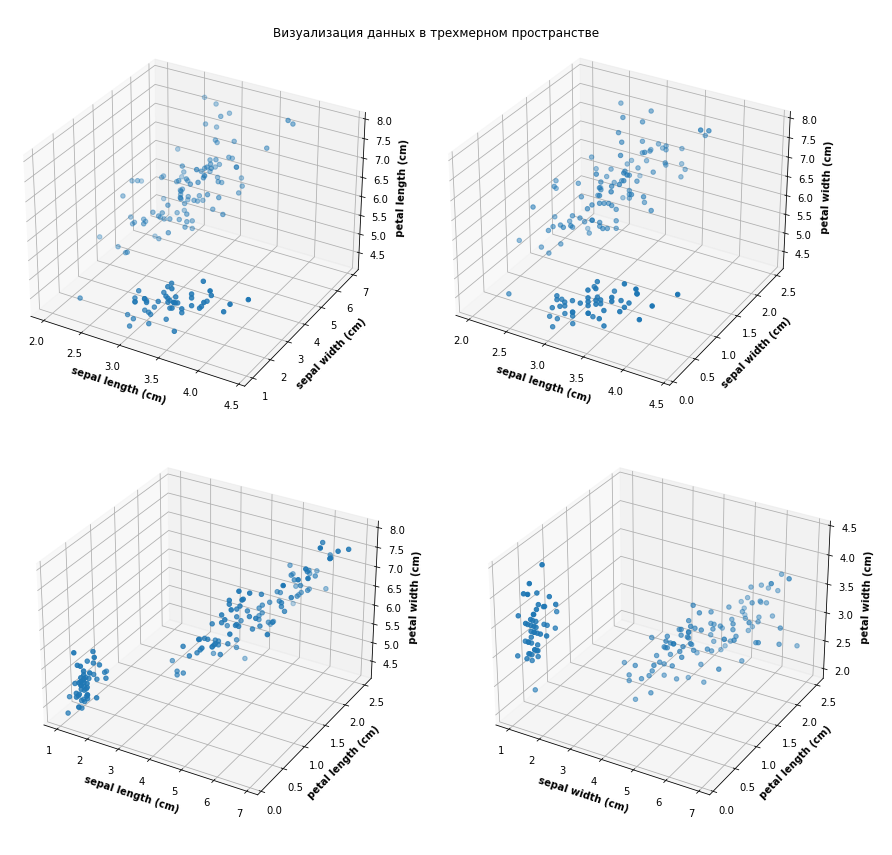
Рис.1 Варианты визуализации данных в трехмерном пространстве
Из возможных вариантов признаков выберу три с наименьшими парными коэффициентами корреляции. При таком условии линейная связь между признаками будет минимальная, а при меньшем влиянии друг на друга мы сможем отобразить более независимые кластеры.
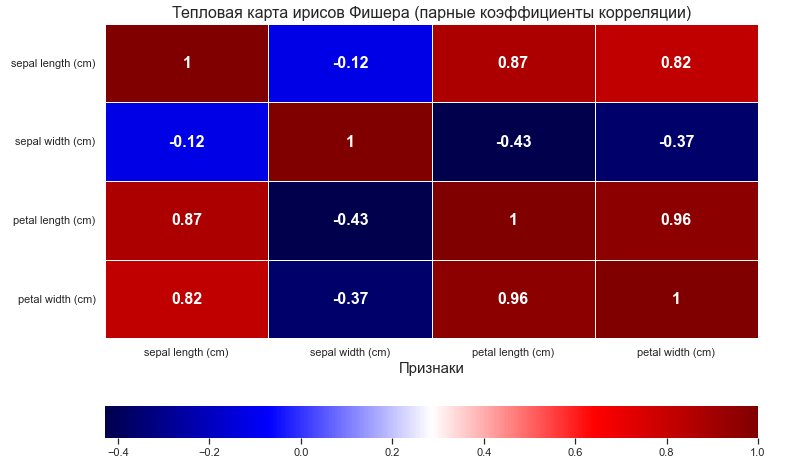
Рис.2 Тепловая карта парных коэффициентов корреляции признаков
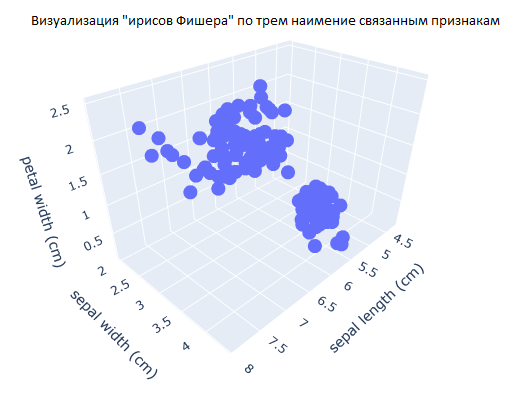
Рис.3 Выбранный вариант визуализации
Из визуального представления понятно, что данные в первую очередь разделяются на две главные группы:
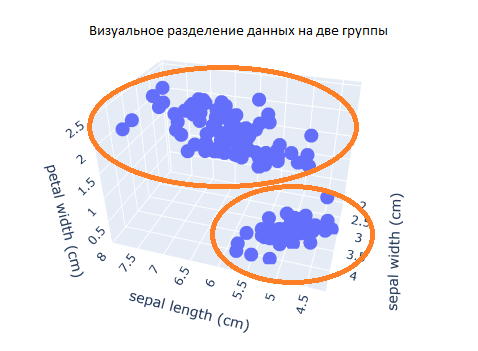
Рис.4 Визуальное разделение данных
Для проведения иерархической кластеризации и исследования зависимости ее результатов от выбора меры близости и правила объединения кластеров сформируем набор диаграмм изменения расстояний при объединении кластеров.
Метрики вносят вклад в форму границ кластеров, но на диаграммах различия в них минимальны. Ниже приведены диаграммы изменения расстояний для евклидового расстояния.
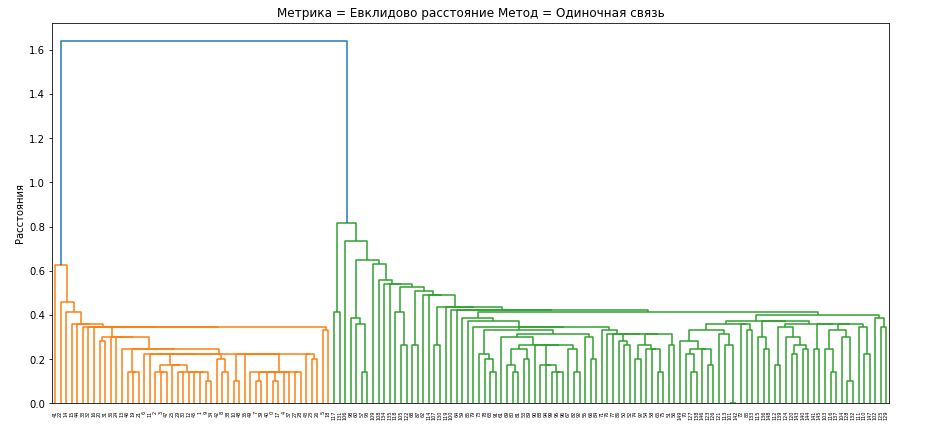
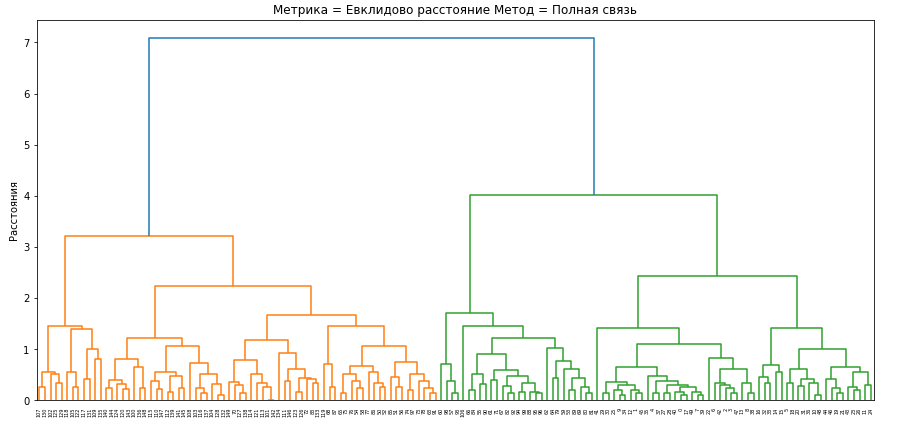
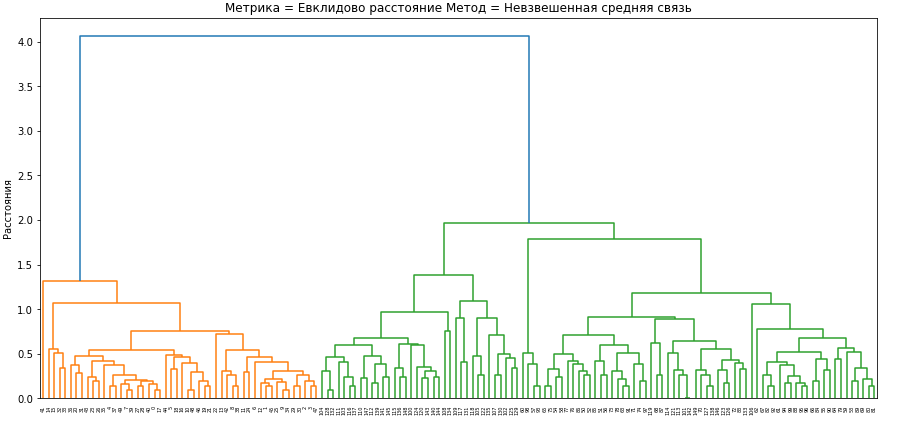
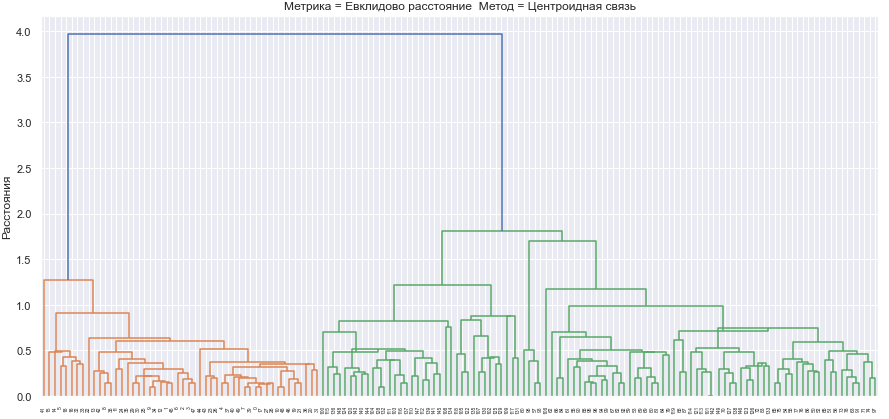
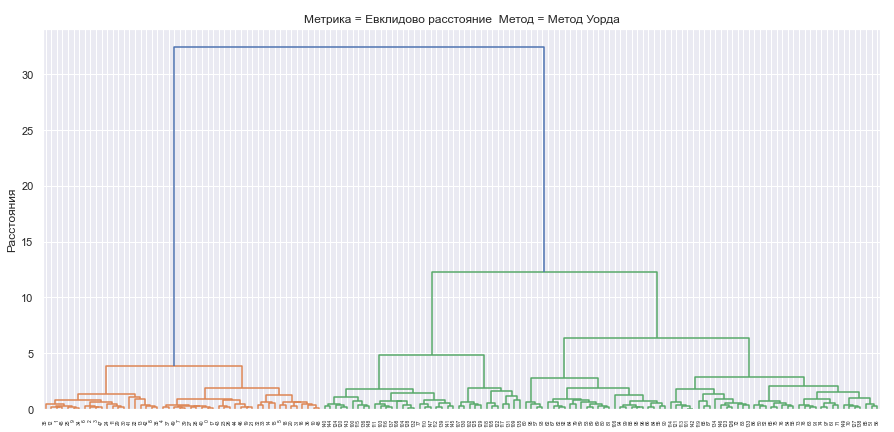
Рис.5-9 Дендрограммы кластеризации выбранными методами
Все методы объединения кластеров показывают, что в наборе данных действительно наблюдаются два главных кластера, один из которых в некоторых методах подразделяется еще на два.
Лучшее разбиение произвелось с помощью метода Уорда, так как три главных кластера определяются на достаточно большом расстоянии, а число шагов объединения визуально меньшее чем у других методов.
Построим проекцию исследуемой совокупности многомерных наблюдений на плоскость с помощью метода главных компонент (PCA).
Метод Главных Компонент (МГК) — один из основных способов уменьшить размерность данных.
Компоненты PCA:
[[ 0.42494212 -0.15074824 0.61626702 0.64568888]
[ 0.42320271 0.90396711 -0.06038308 -0.00983925]
[-0.71357236 0.33631602 -0.0659003 0.61103451]
[-0.36213001 0.21681781 0.78244872 -0.45784921]]
Ковариционная матрица:
[[ 0.05290845 -0.00491134 0.05999602 0.05975355]
[-0.00491134 0.03298254 -0.02328082 -0.02111795]
[ 0.05999602 -0.02328082 0.08952249 0.09149784]
[ 0.05975355 -0.02111795 0.09149784 0.10086914]]
Доля от общей дисперсии: [0.84136038 0.11751808 0.03473561 0.00638592]
[0.84136038 0.11751808]
Сумма равна 0.9588784639918416
Две главные компоненты несут в себе более 95% информации
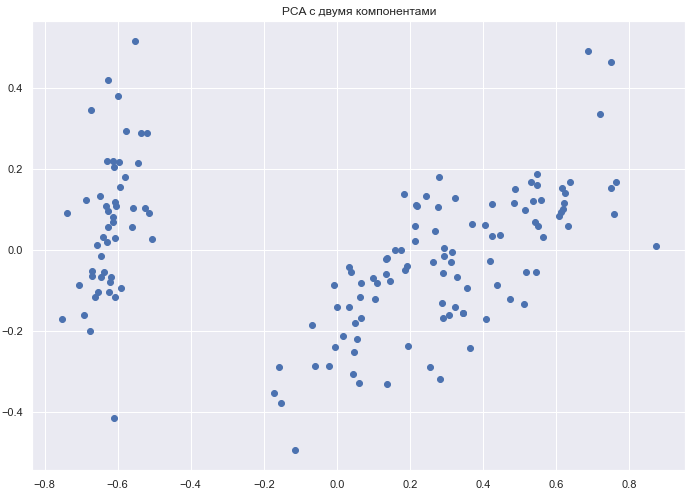
Рис.10 Проекция выборки на двухмерное пространство методом главных компонент.
Построим проекцию исследуемой совокупности многомерных наблюдений на плоскость с помощью стохастического вложения соседей с t-распределением (t-sne).
Понижение размерности методом t-sne.
t-sne — это инструмент для визуализации многомерных данных. Он преобразует сходства между точками данных в совместные вероятности. t-SNE имеет весовую функцию, которая не является выпуклой, т.е. при разных инициализациях мы можем получить разные результаты.
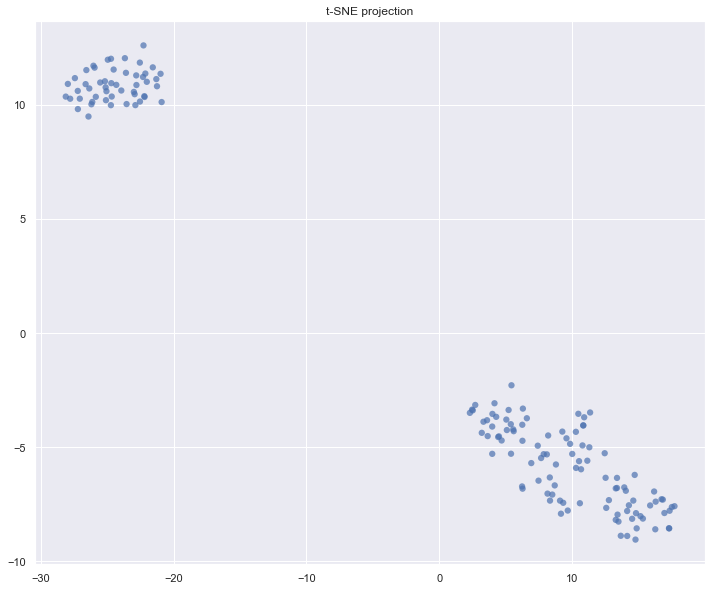
Рис.11 Проекция выборки на двухмерное пространство методом t-sne.
Можем сделать вывод о том, что в выборке имеются два главных кластера, более крупный из которых подразделяется еще на два. Используя результаты кластеризации методом Уорда можно заявить о наличии 3 главных кластеров на одном уровне разделения.
Проведем неиерархическую кластеризацию с помощью центроидного метода k-средних:
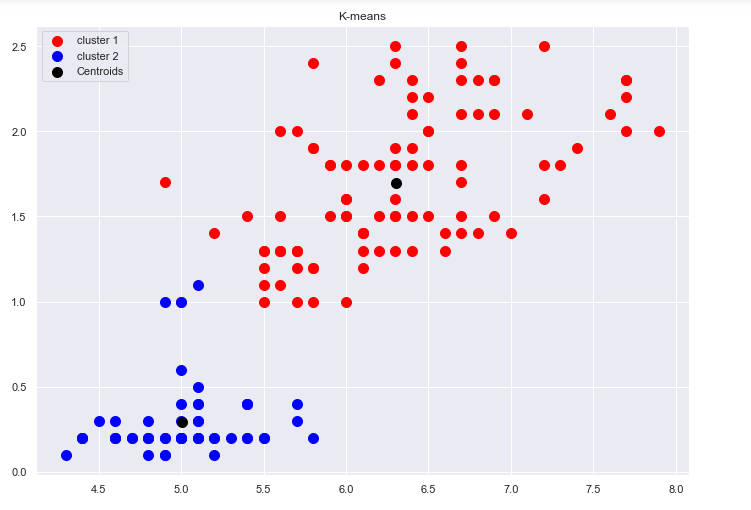
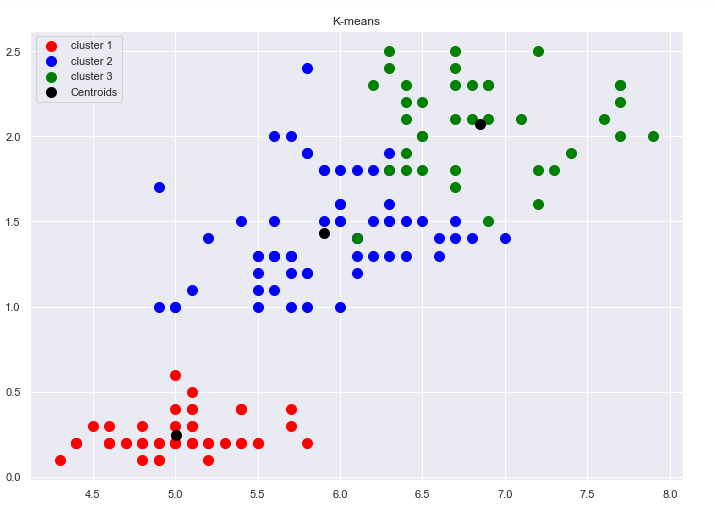
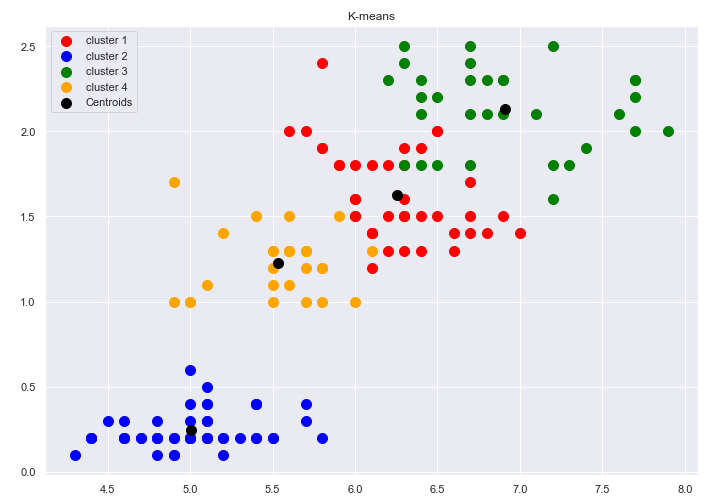
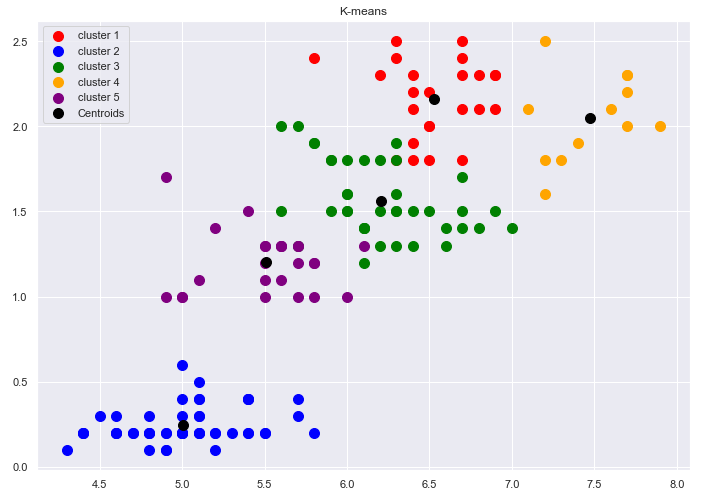
Рис.12-15 Отображения на плоскость результатов неиерархической кластеризации на 2,3,4,5 кластеров.
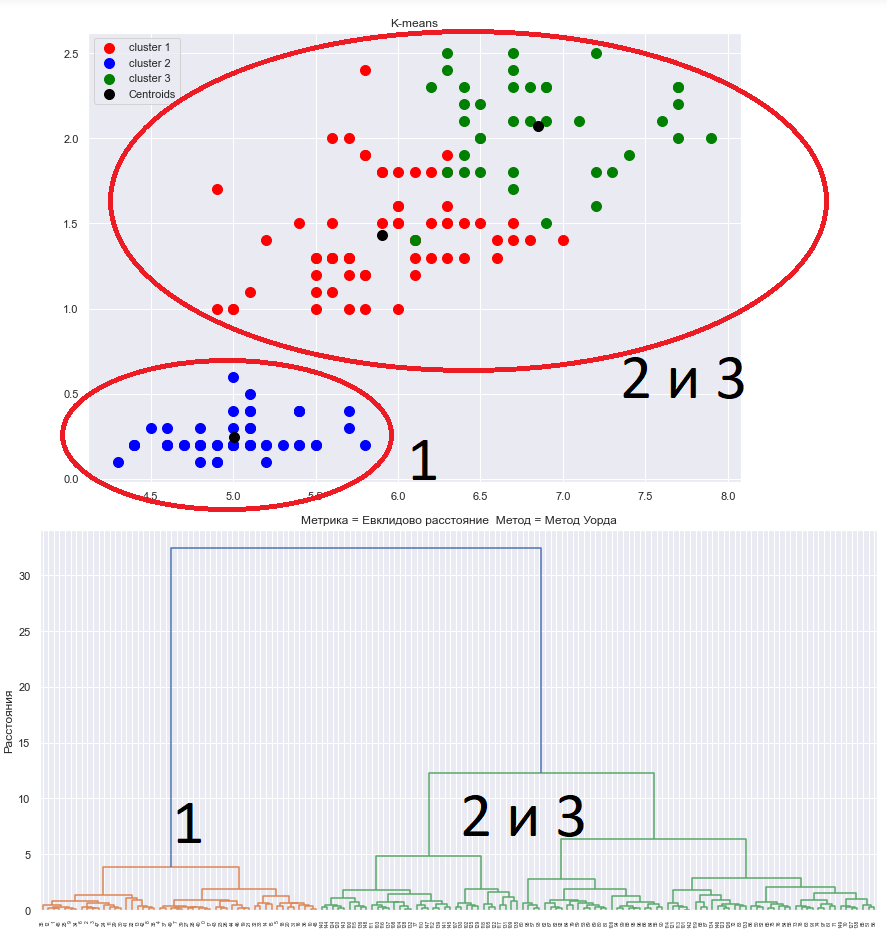
Рис.16 Визуальное определение числа кластеров
Сравним данные полученные с помощью неиерархической кластеризации с настоящими видами цветов.

Рис.17 Визуализация реальных видов цветов
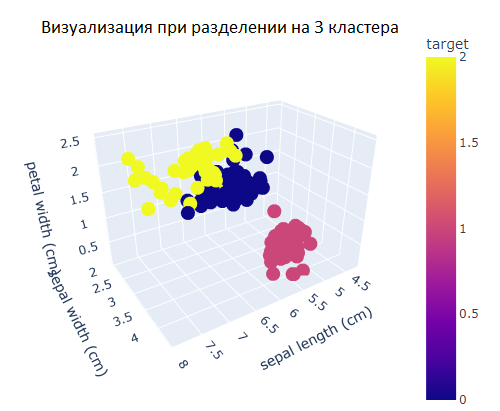
Рис.17 Визуализация разделения на 3 кластера
Можно сделать вывод о том, что выборка разделяется на два главных кластера достаточно однозначно, на практике в отличие от реального значения видов цветов мы имеем некоторые расхождения по группировке объектов по близости расположения с помощью метода k-средних. Это видно по различию действительного распределения видов и полученному разделению верхнего кластера на визуализациях.
Результаты неиерархическая кластеризации подтверждают предположения, которые были сделаны ранее.
Для выборки «Рост-Вес-Возраст-Позиция»
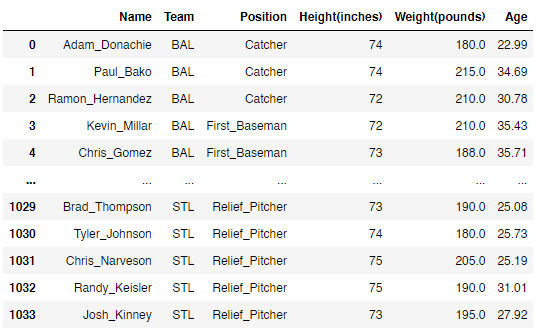
Рис.17 Представление данных
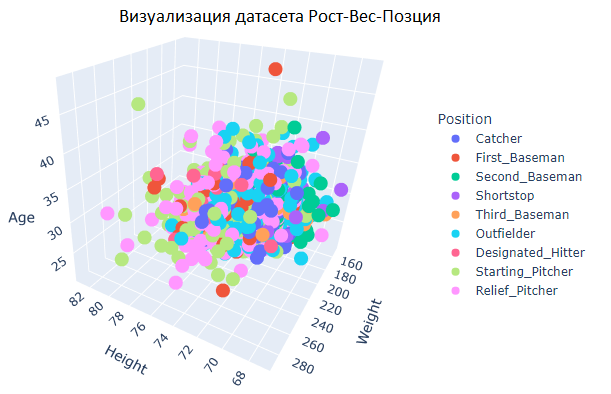
Рис.18 Визуализация данных
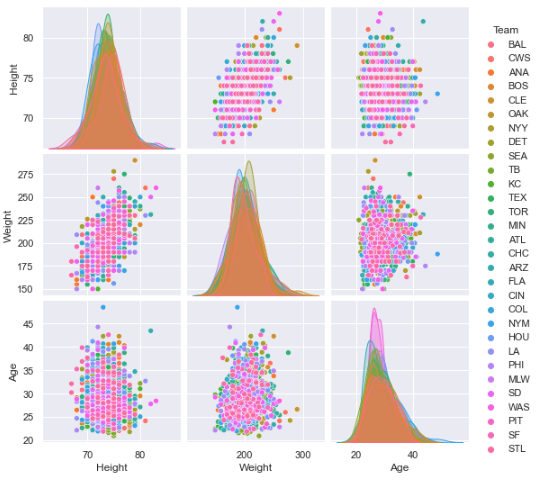
Рис.18 Информация о распределениях параметров
На рисунках видно, что имеется сильное пересечение признаков.
Разделить параметры не представляется возможным.
