
нир / ЛР1_А-02-20_2бригада
.docxФедеральное государственное бюджетное образовательное учреждение высшего образования. «Национально исследовательский университет
«Московский энергетический институт»
Кафедра Управления и интеллектуальных технологий
Лабораторная работа №1
ИССЛЕДОВАНИЕ КОМБИНАТОРНЫХ ЛОГИЧЕСКИХ СХЕМ
Курс: Функциональные узлы и схемотехника систем управления и вычислительных машин
Выполнили: 2 бригада
Аношкин Д.В.
Дашин И.Н.
Москва 2022 г.
Цель работы состоит в ознакомлении с основами функционирования базовых логических элементов, правилами преобразования логических функций, построения и реализации комбинаторных логических схем, а также в изучении симулятора Deeds и получении практических навыков работы с ним.
Таблица 1 – Представление КЛС для реализации в лабораторной работе (бригада 2)
a |
b |
c |
d |
Y2 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
По таблице построили выражение логической функции в несовершенной дизъюнктивной нормальной форме.
Y=
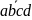 +
+
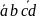 +
+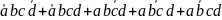 +
+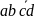
Схемная реализация с использованием переключателей входных сигналов:
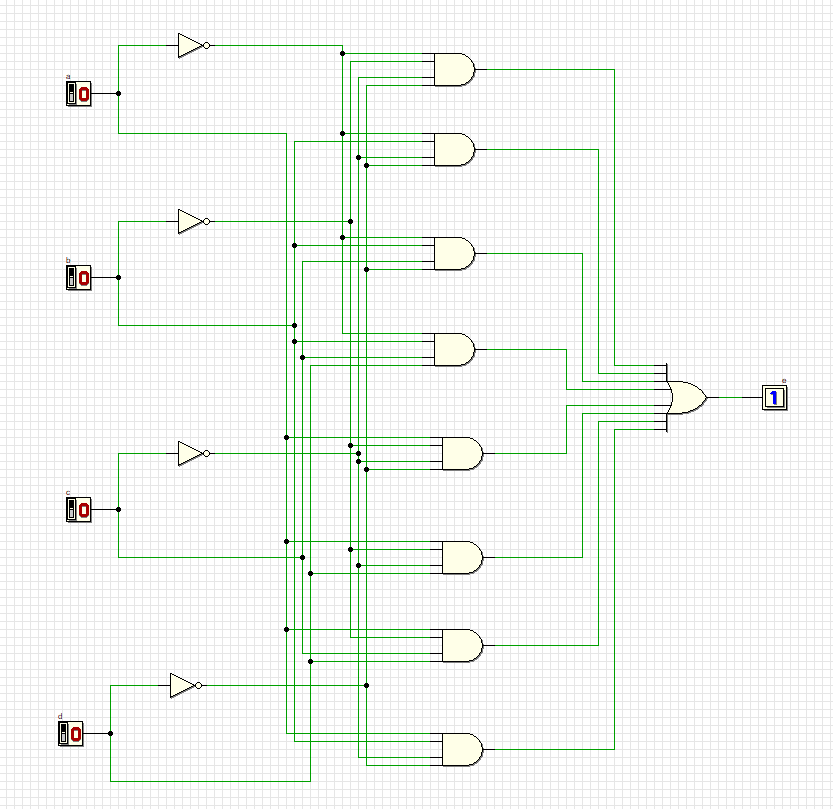
Проверка всех комбинаций:
1
2
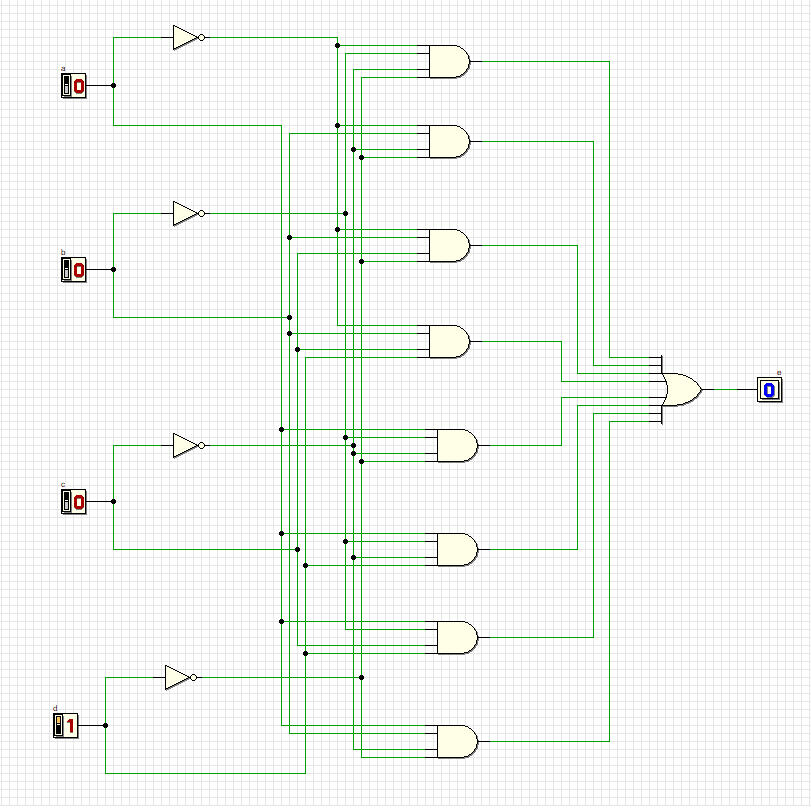
3
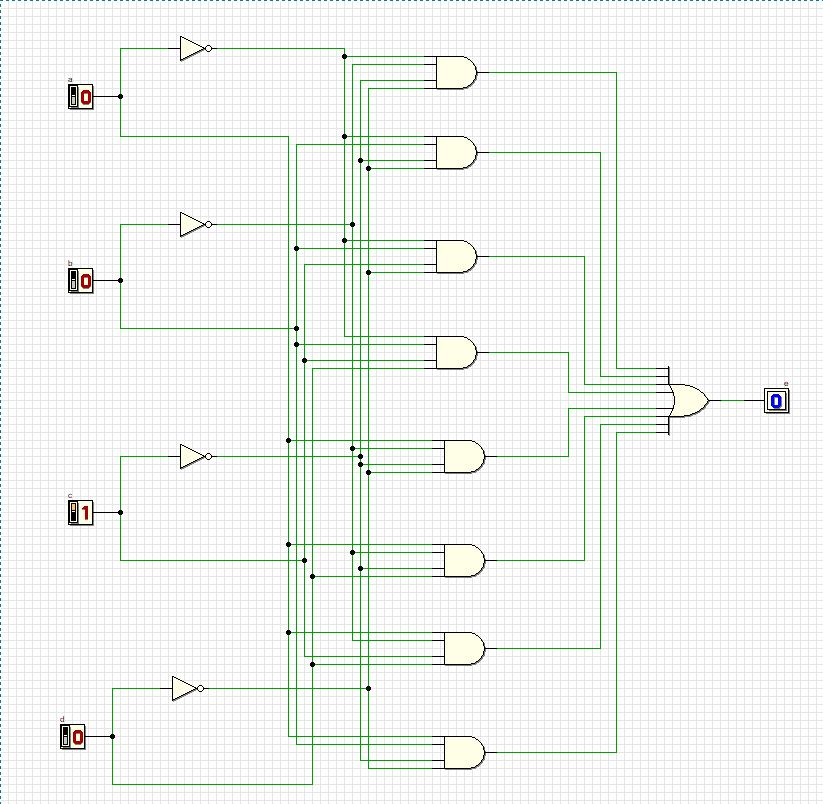 4
4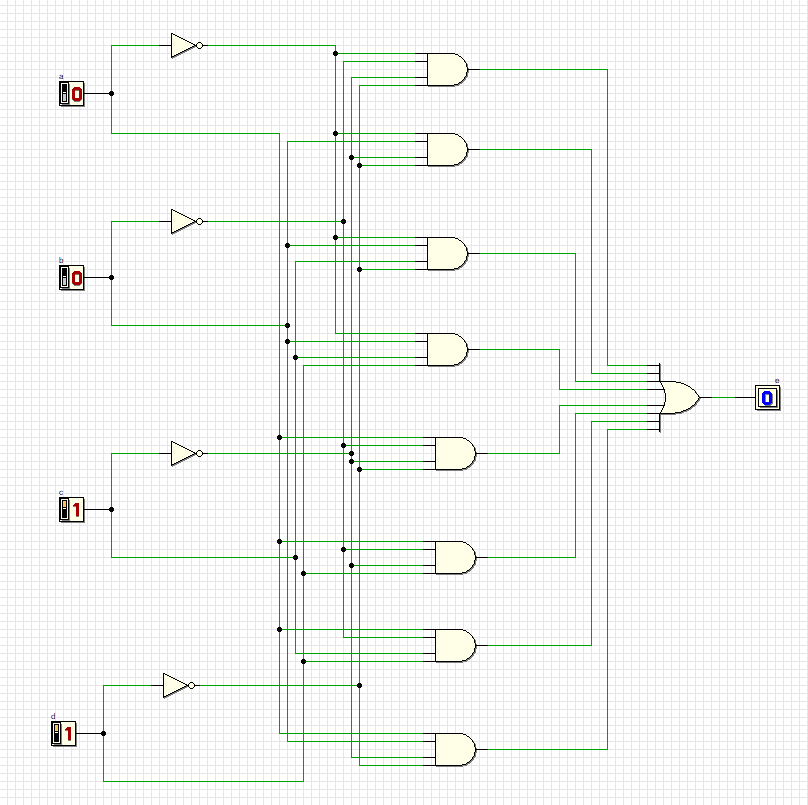
5
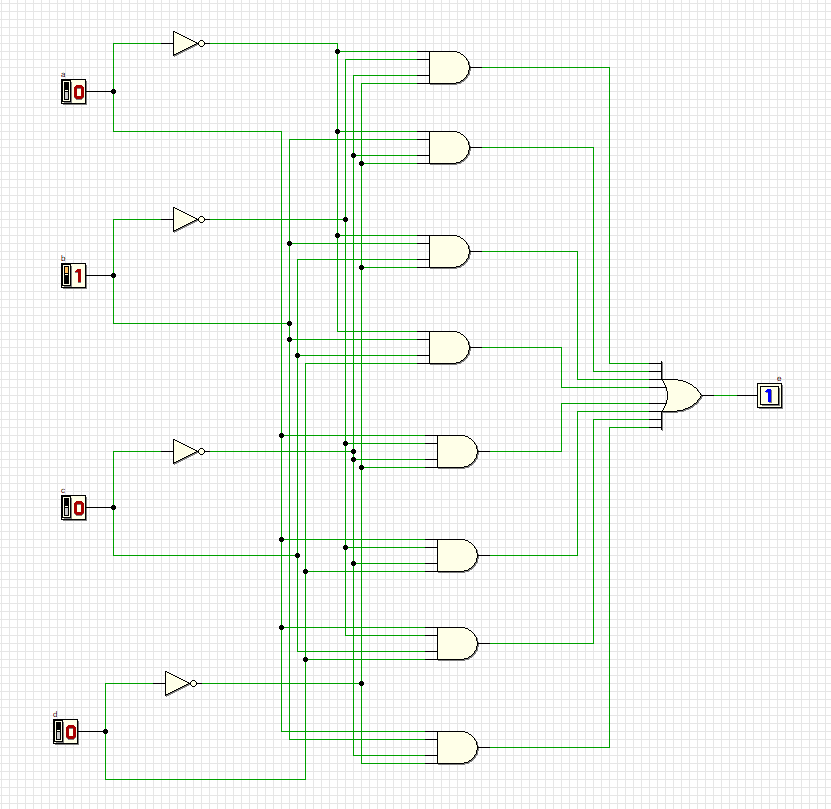
6
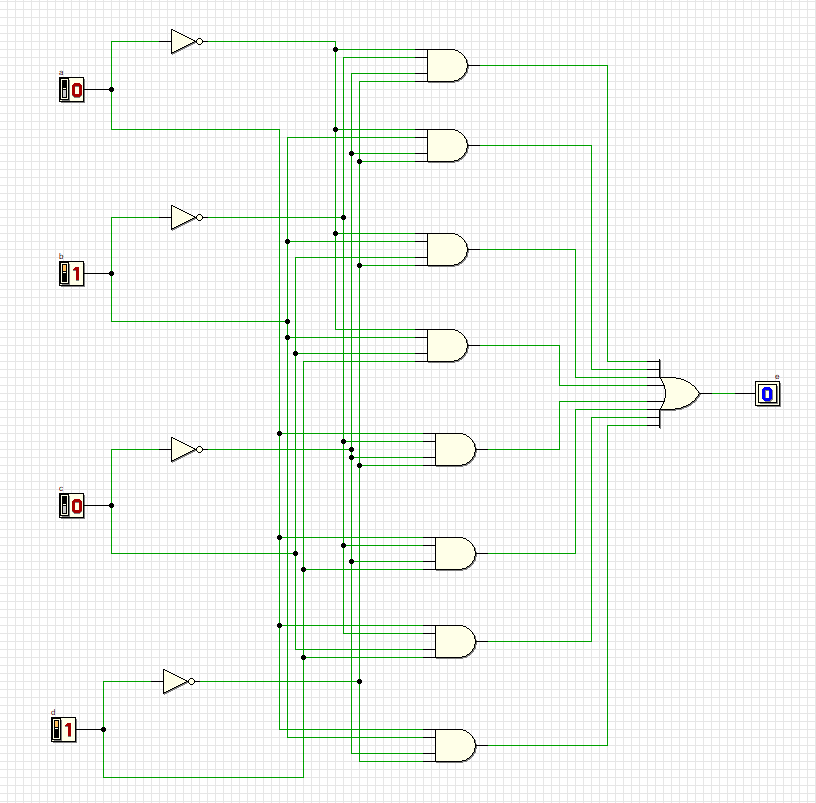
7
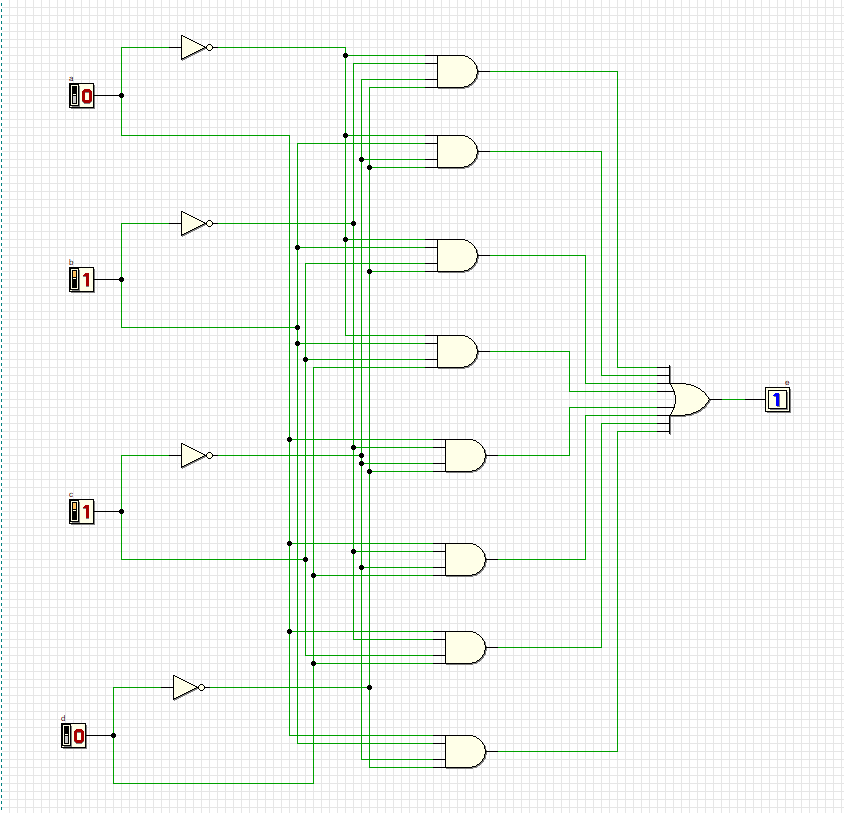
8
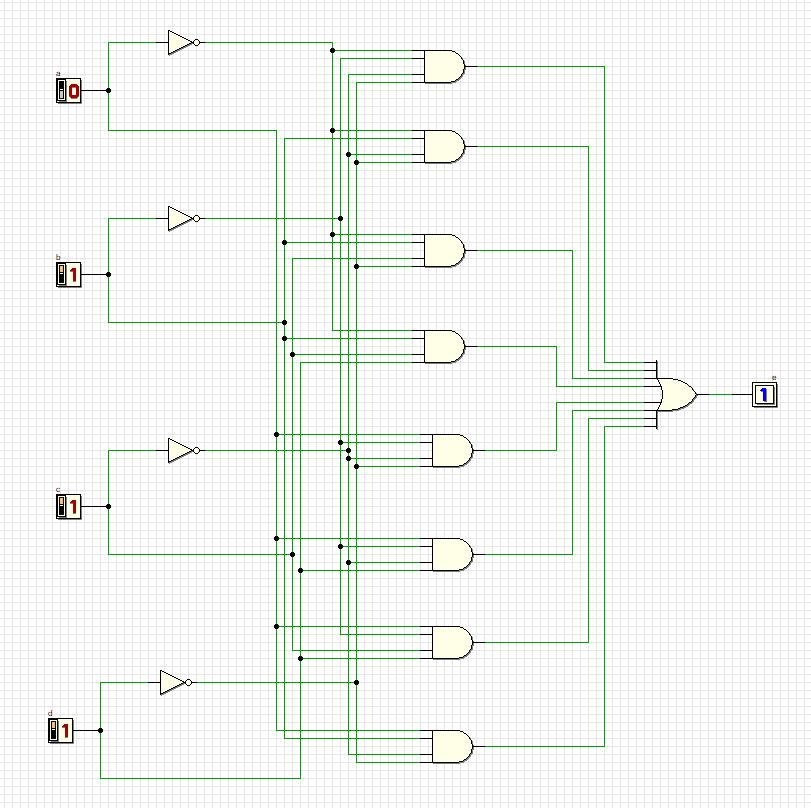
9
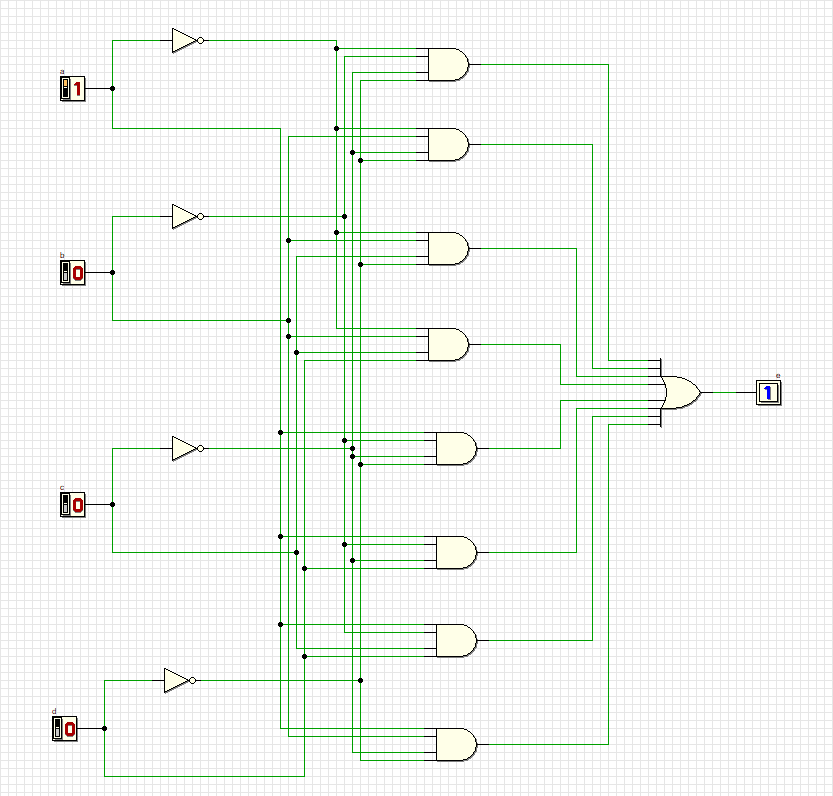
10
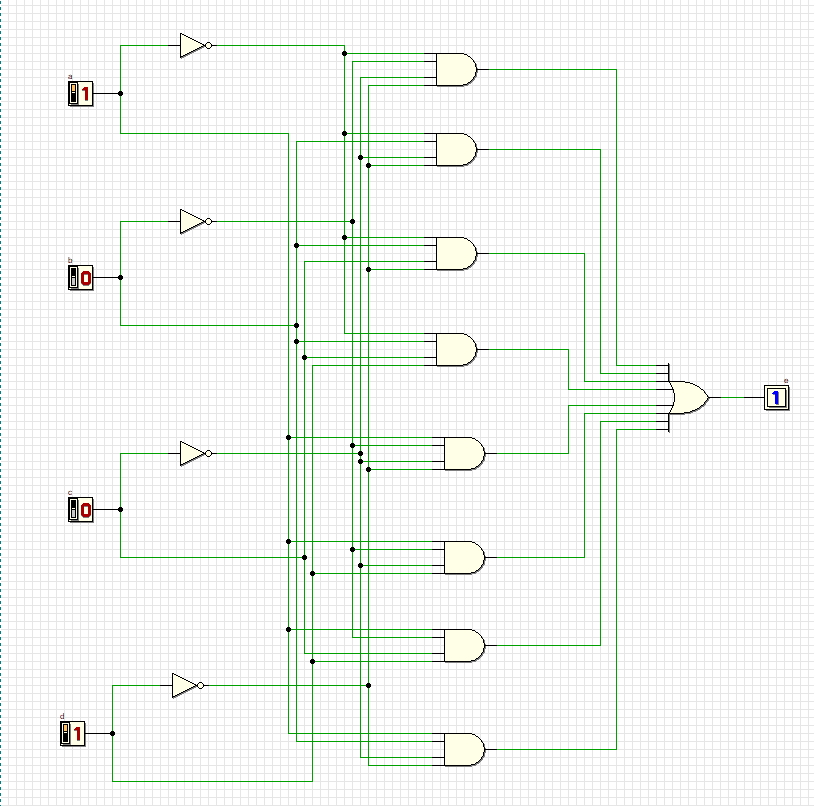
11
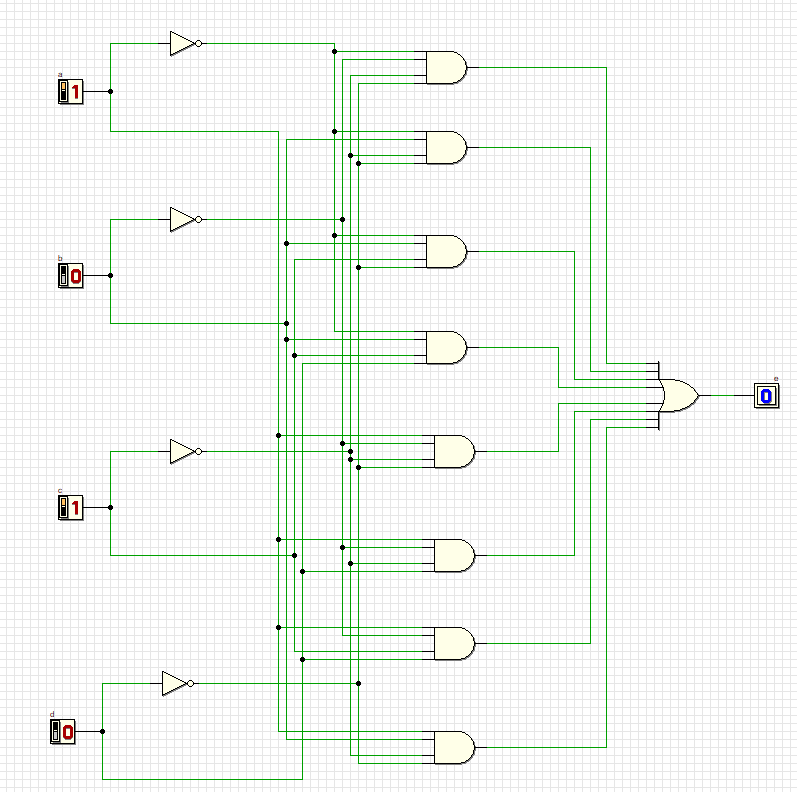
12
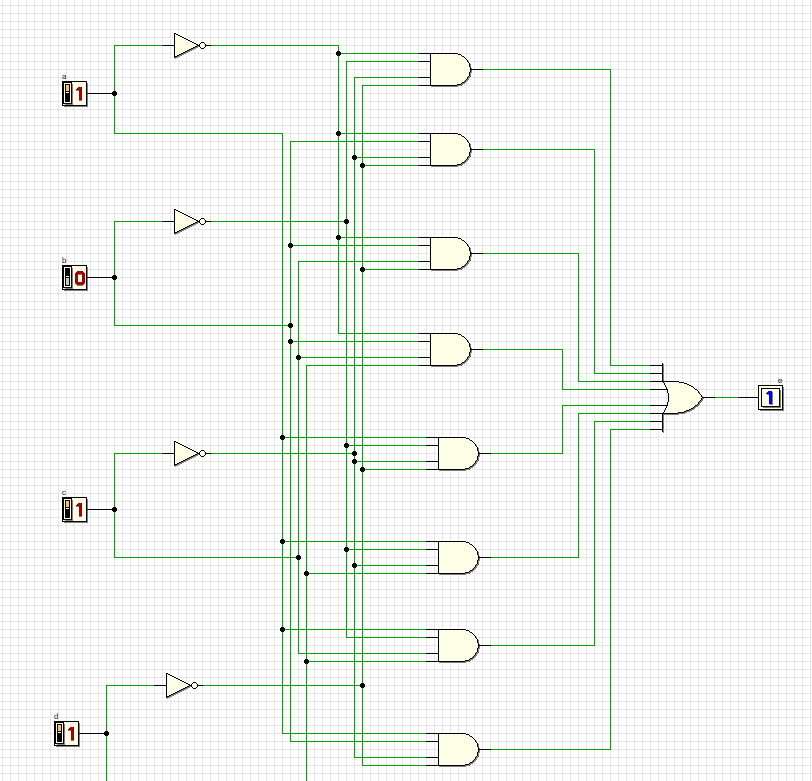
13
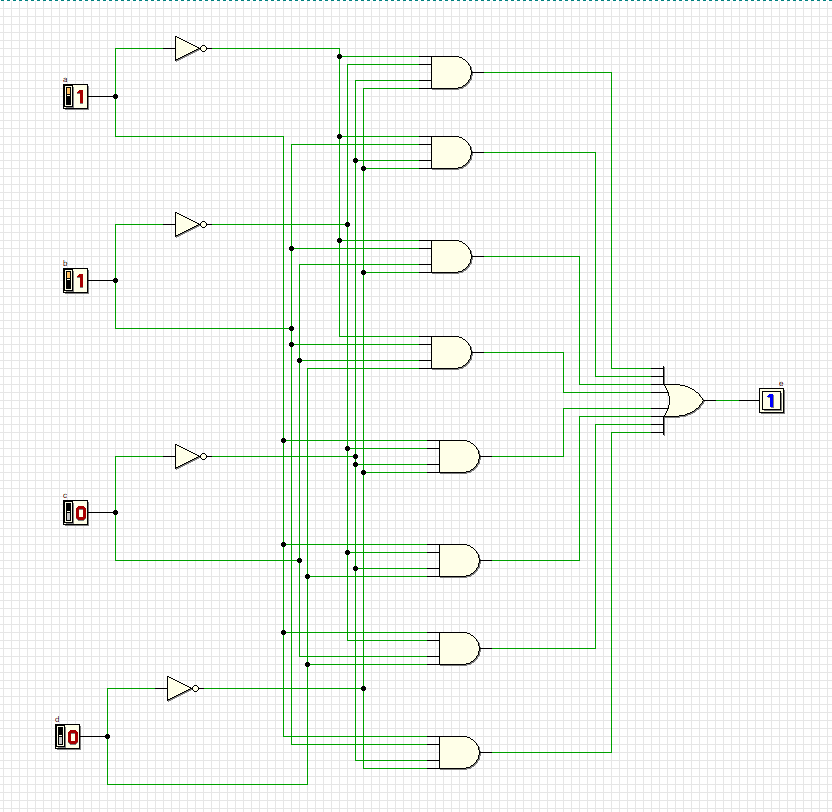
14

15
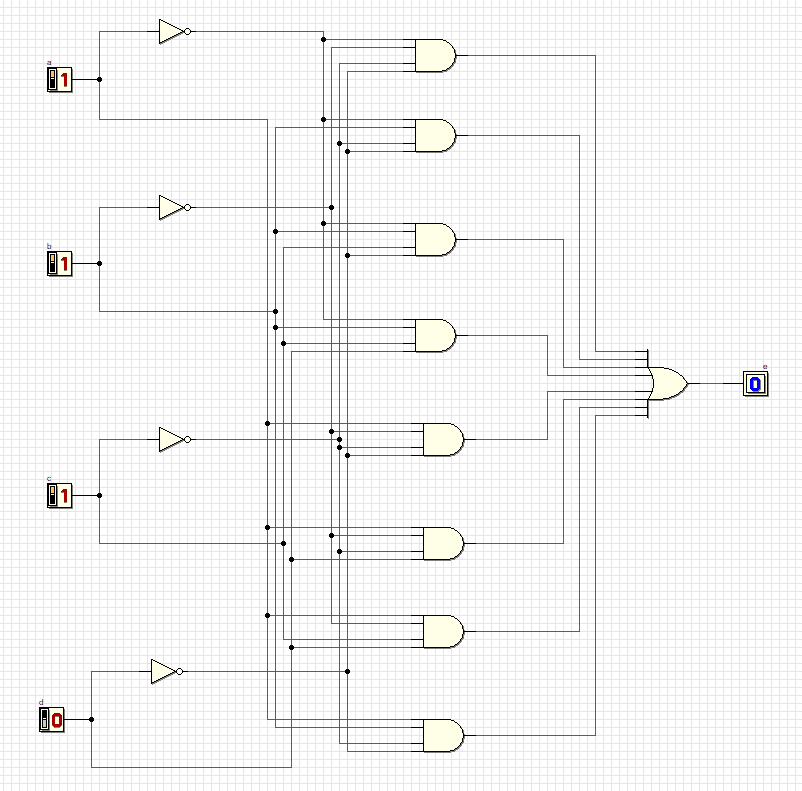
16
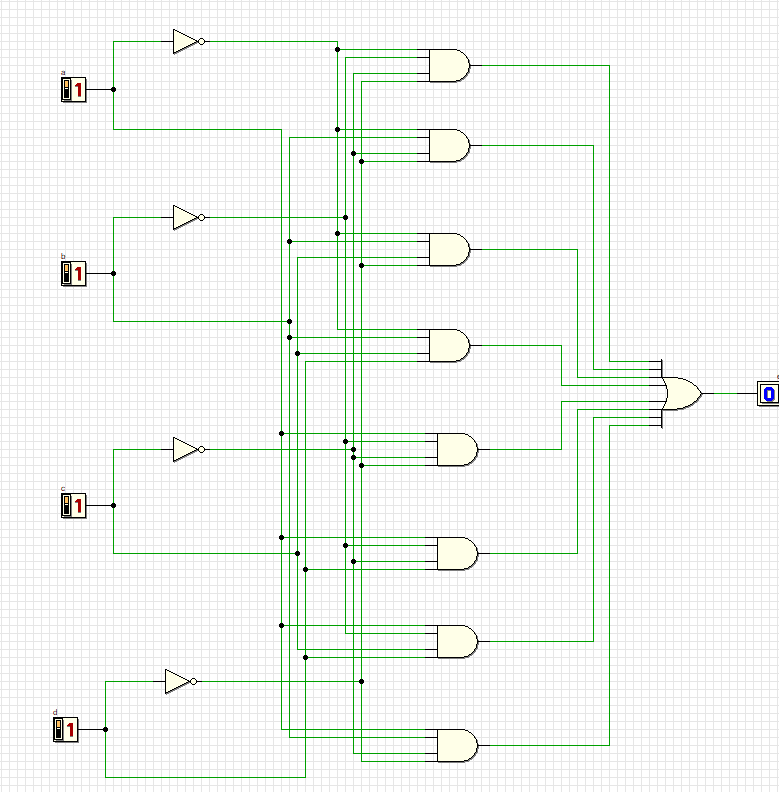
Схема удовлетворяет всем комбинациям.
Задаем каждый входной сигнал на КЛС (a, b, c, d), как сигналы с собственного генератора.
При таком построении частот генераторов на входе КЛС сформируется последовательность входных сигналов, в которой последовательно будут переключаться все 16 комбинаций входных сигналов
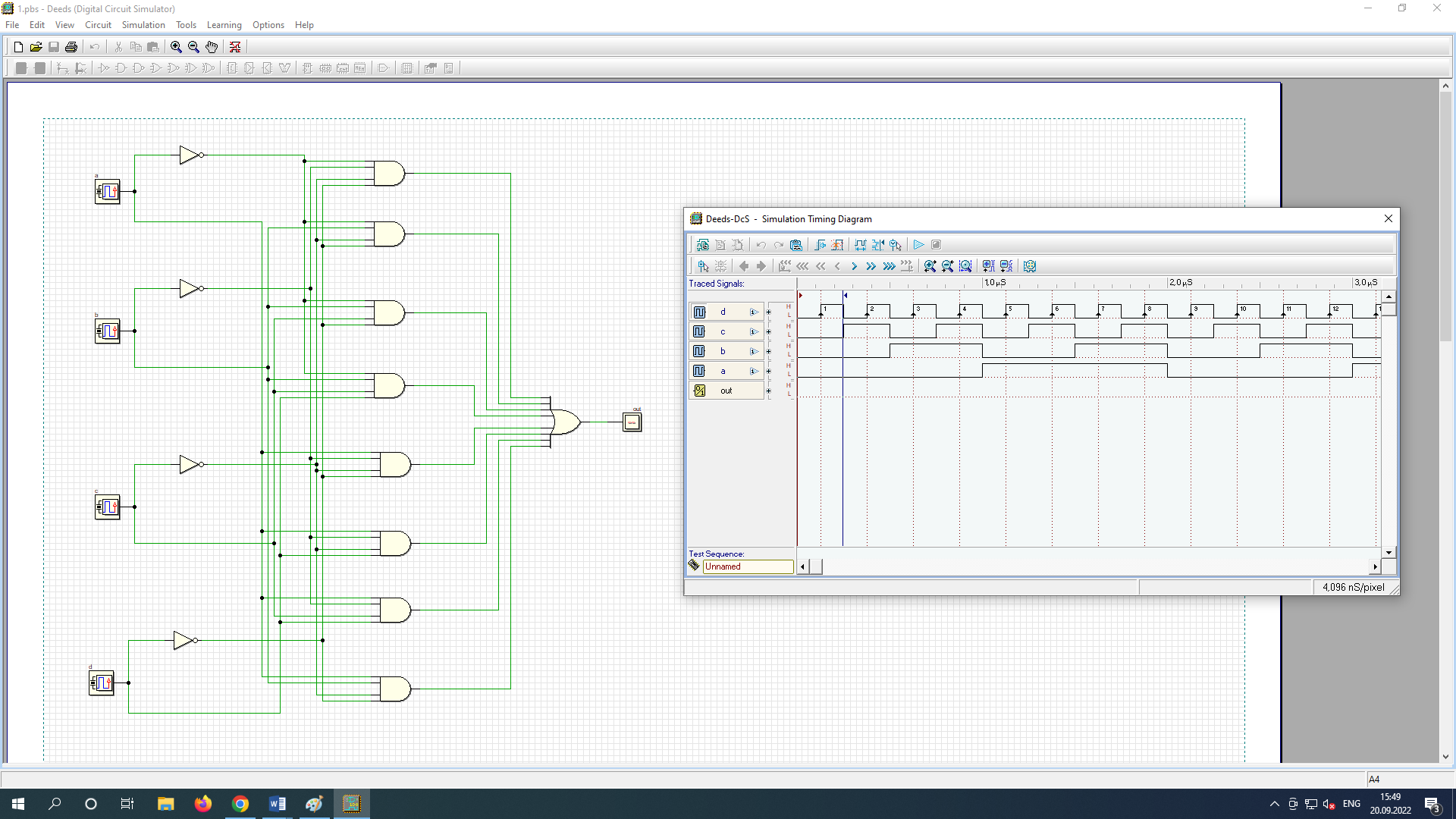
Преобразовали полученное выражение в совершенную дизъюнктивную нормальную форму.
Y=
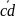 +
+
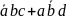
Проверяем комбинации новой схемы:
1

2
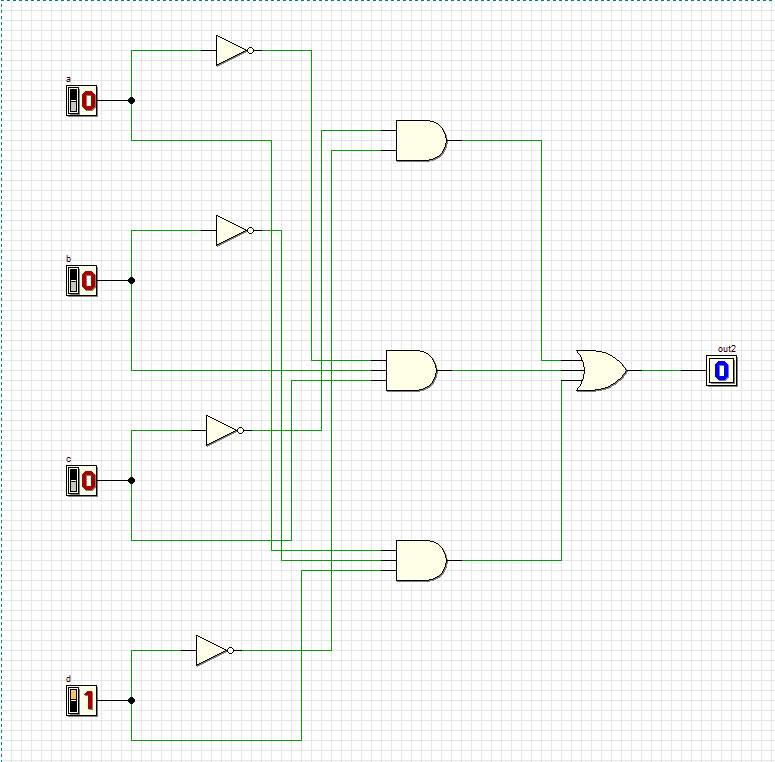
3
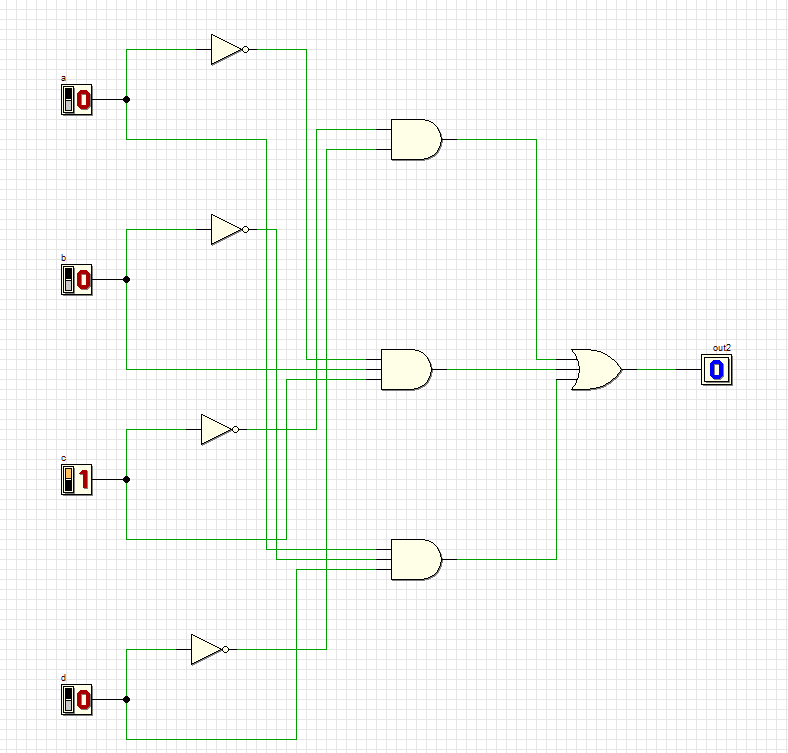
4
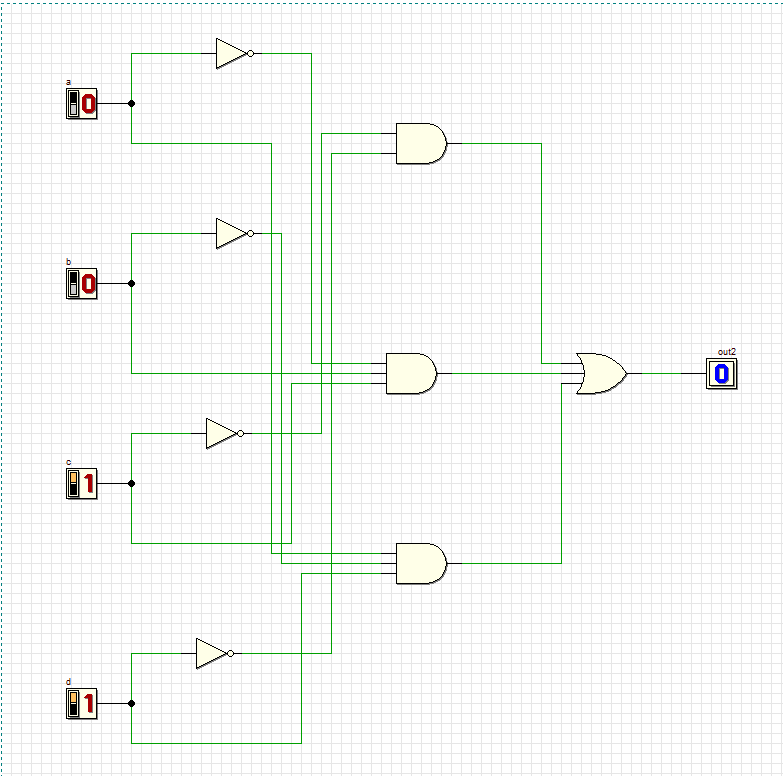
5
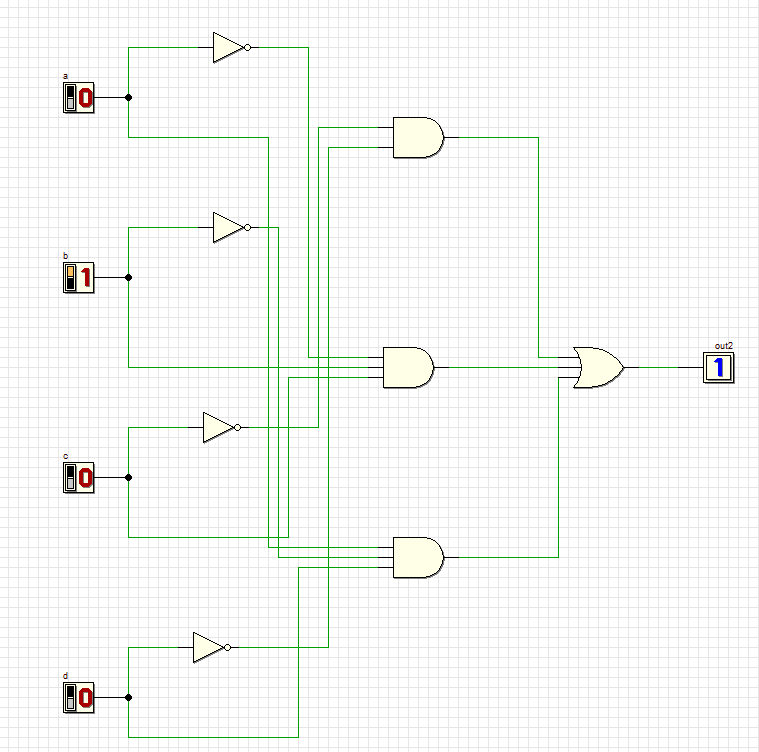
6
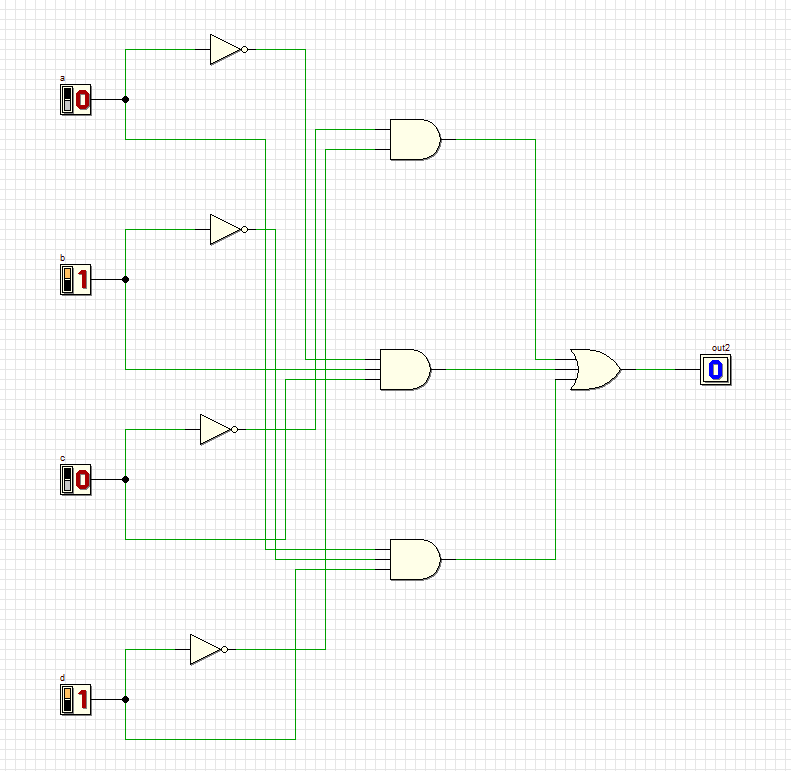
7
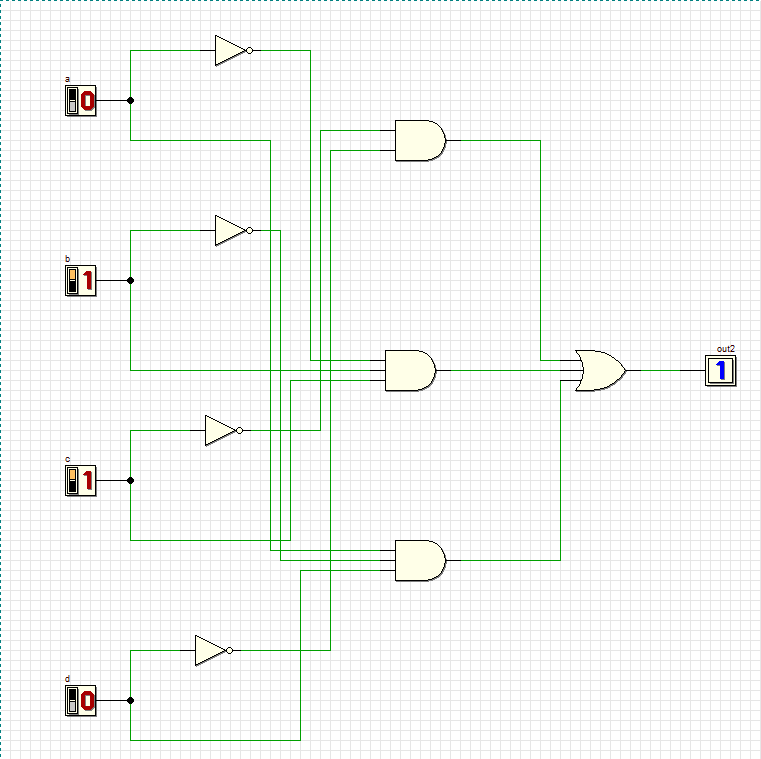
8
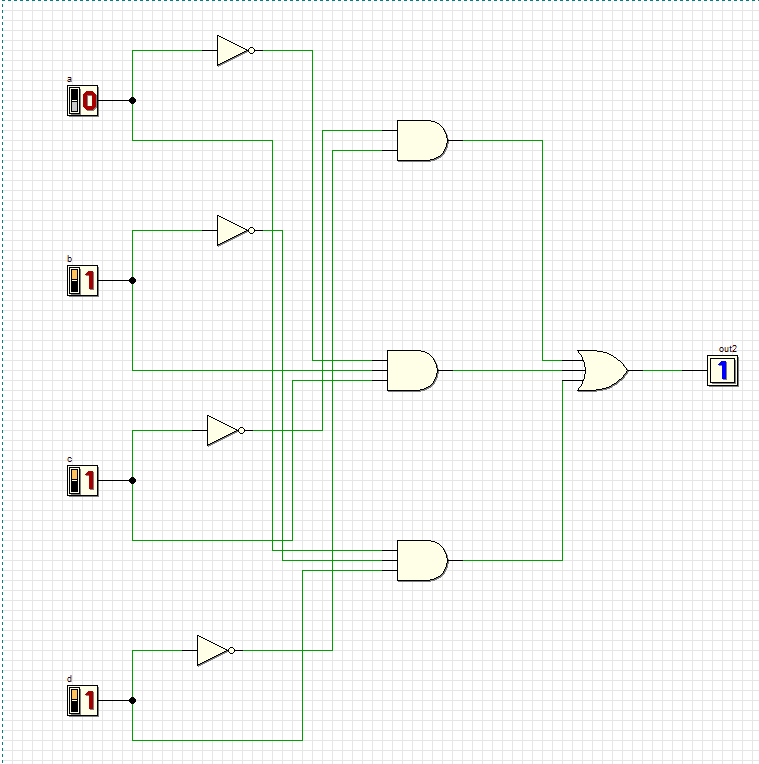
9
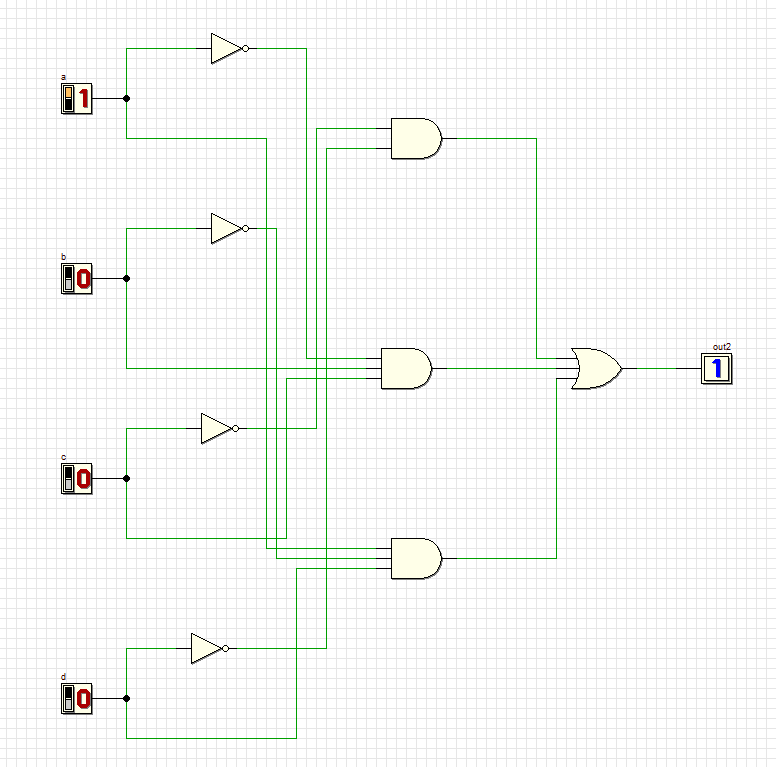
10
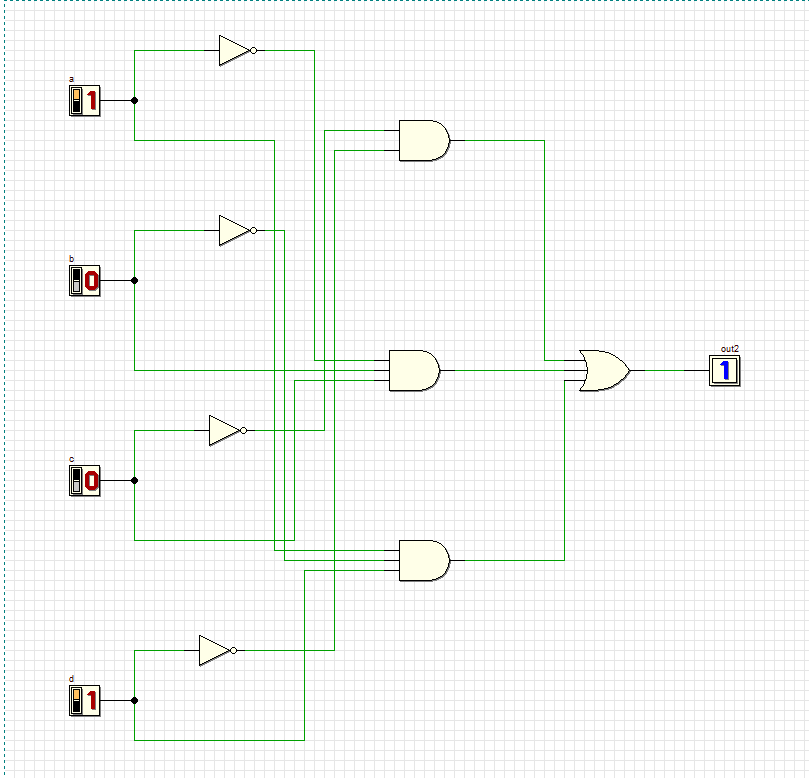
11
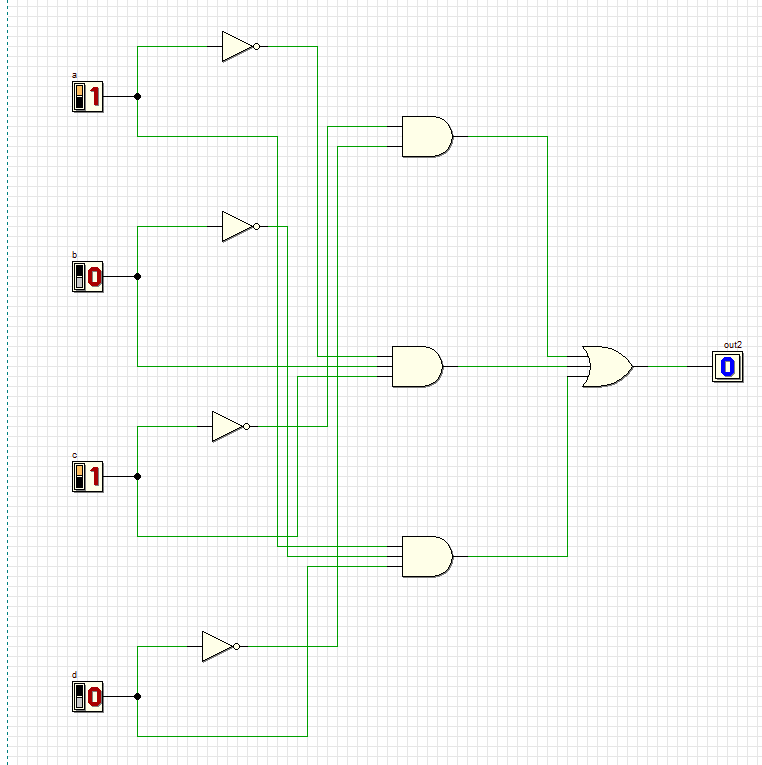
12
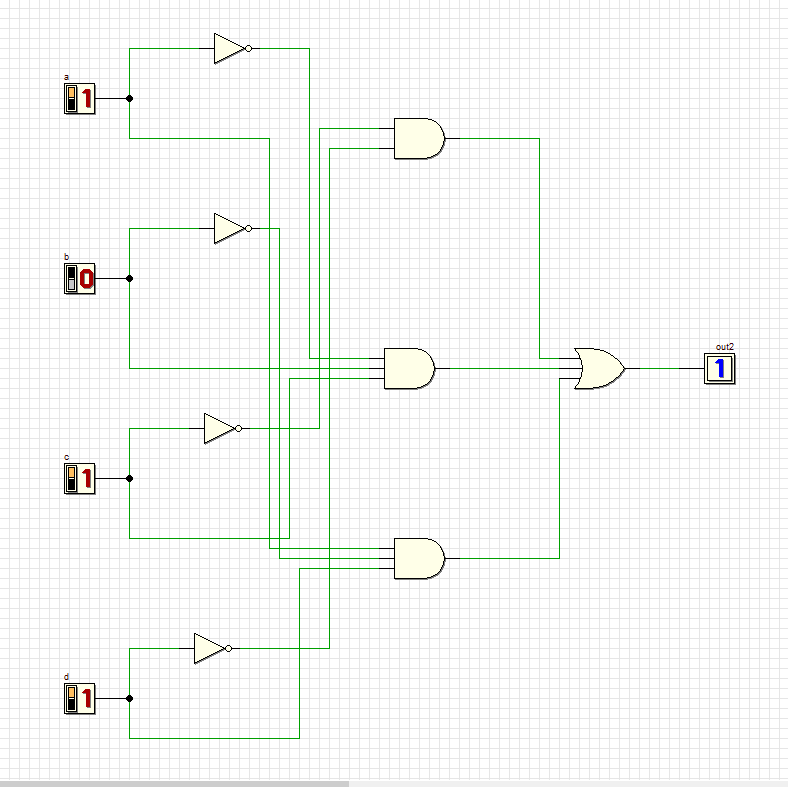
13

14
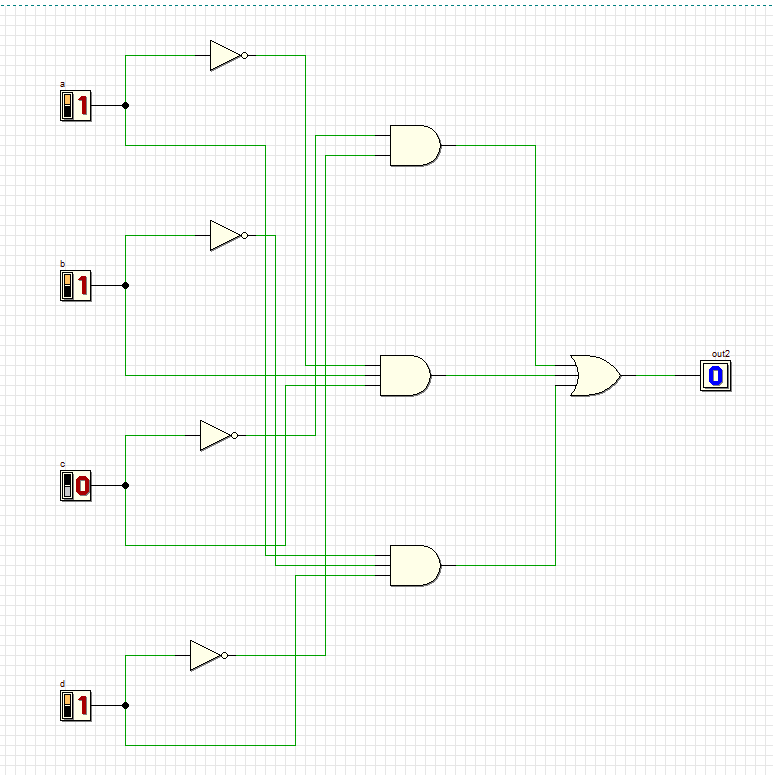
15
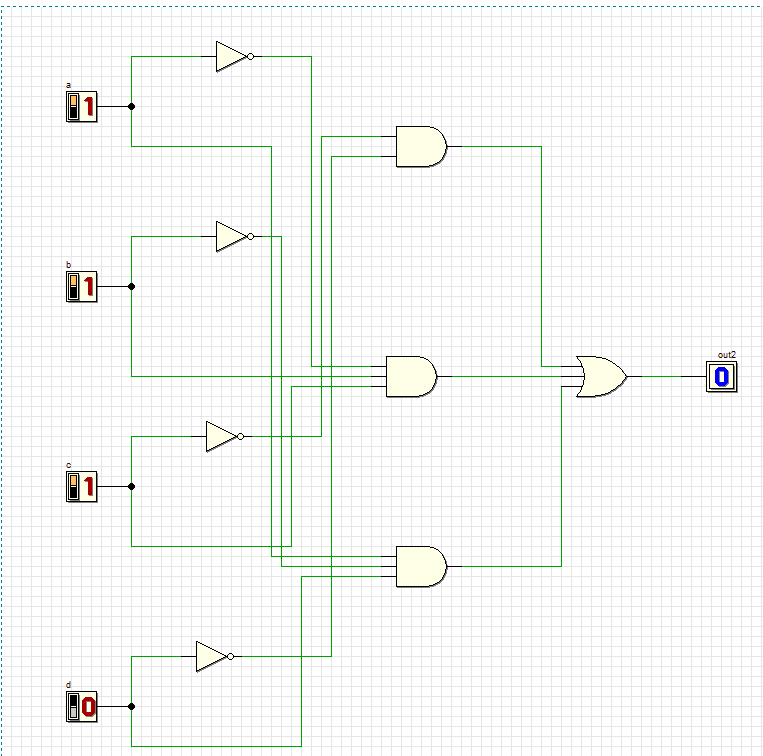
16
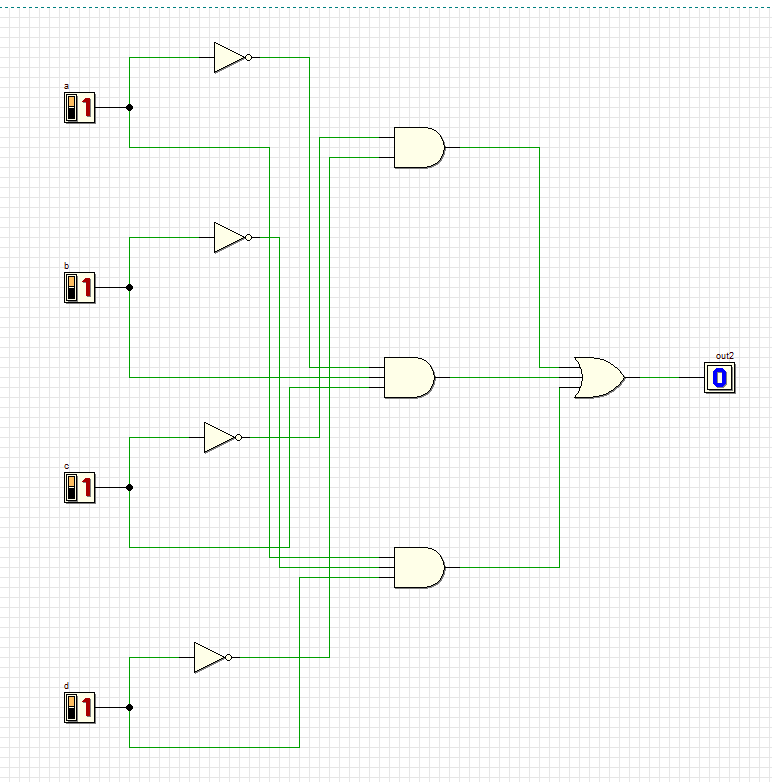
Все комбинации соответствуют таблице.
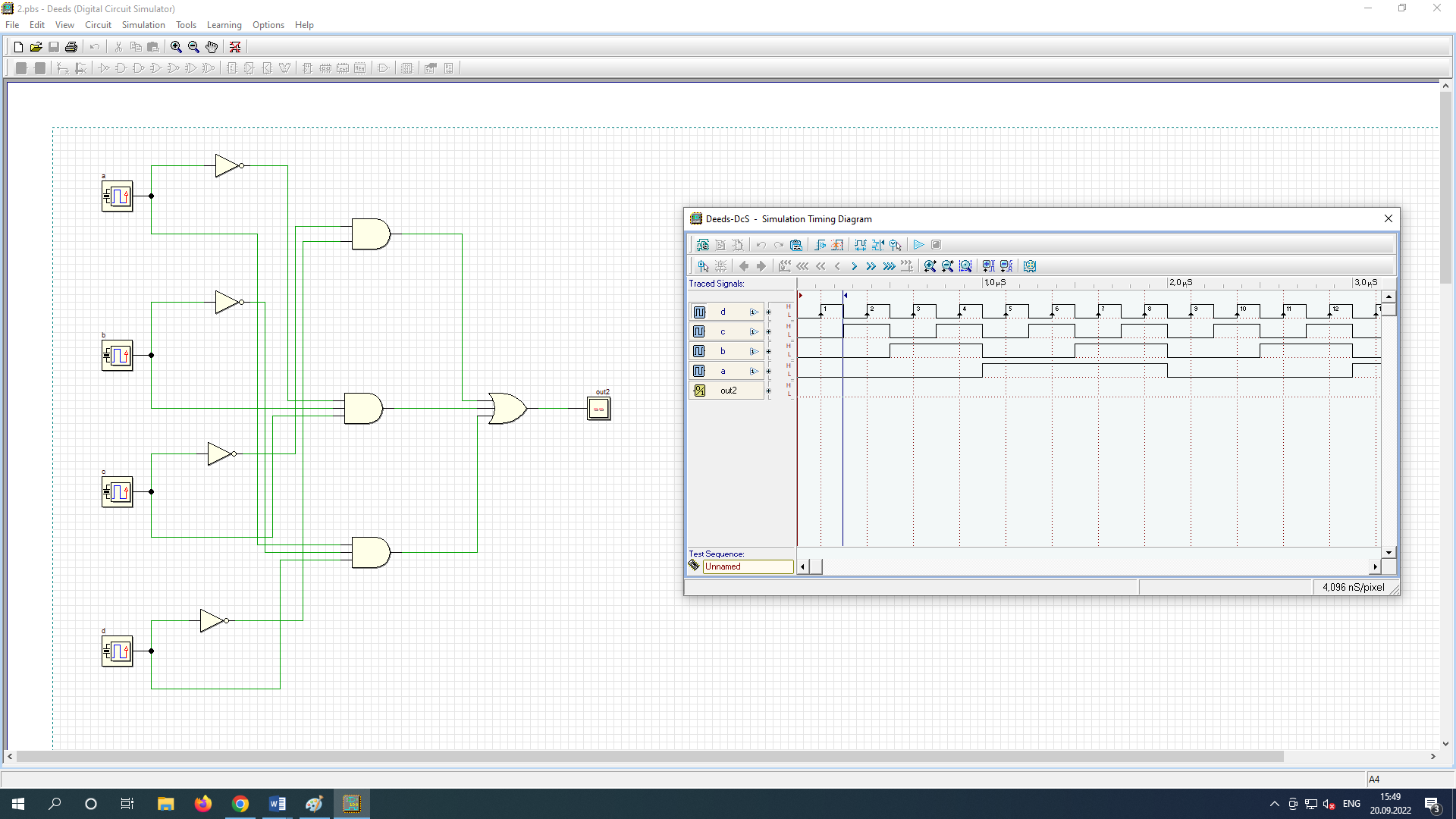
Вывод: Получаем на 5 логических элементов меньше при реализации в совершенной дизъюнктивной нормальной форме (по сравнению с реализацией КЛС в простой дизъюнктивной нормальной форме).
